HoudiniVex笔记_P16_GeometruFunction几何体函数

原视频：https://www.youtube.com/playlist?list=PLzRzqTjuGIDhiXsP0hN3qBxAZ6lkVfGDI
Bili：Houdini最强VEX算法教程 - VEX for Algorithmic Design_哔哩哔哩_bilibili

Houdini版本：19.5

先复习下几何体属性Vertex、Point、Primitive、Detail之间的关系，如下图，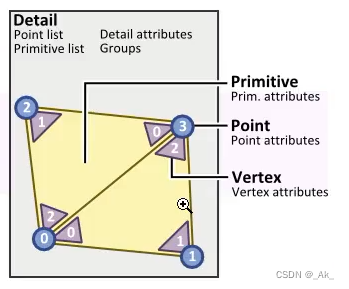

1、添加点

eg.创建类型为Detail的AttributeWrangle节点，写入如下代码，

int pt = addpoint(0, set(0, 0, 0));     //原点添加一个点
setpointattrib(0, 'num', pt, pt+1);     //对点添加属性，属性命名为 num，值为1

结果为：在场景的原点处创建了一个点，其在表格中为：

2、创建螺旋点

eg.创建类型为Detail的AttributeWrangle节点，写入如下代码，

float ang = chf('ang') * $PI;   //角度值float steplen = chf('len');for(int i=0; i<chi('num'); i++){float x = cos(i * ang);     //x坐标float z = sin(i * ang);     //z坐标float y = i * 0.1;          //每次循环高度递增vector pos = set(x, y, z) * steplen;    //相当于缩放int pt = addpoint(0, pos);  //创建点
}

结果：在 Ang=0.1，num=0.2，num=100 条件下，（为排版美观，图已旋转）

3、绘制多边形

eg.创建一个三角形，把360°均分，每120°创建一个点，然后连接起来。
操作：创建类型为Detail的AttributeWrangle节点，写入如下代码，

float ang = chf('ang') * $PI * 2.0;    //初始点的角度值int pt1 = addpoint(0, set(cos(ang), 0.0, sin(ang)));
int pt2 = addpoint(0, set(cos(ang + radians(120.0)), 0.0, sin(ang + radians(120.0))));
int pt3 = addpoint(0, set(cos(ang + radians(240.0)), 0.0, sin(ang + radians(240.0))));int poly = addprim(0, 'poly', pt1, pt2, pt3);

结果：滑动ang值，三角形旋转，

4、创建锥形

先创建锥形底面，底面的点与顶点依次连接。

 eg.创建类型为Detail的AttributeWrangle节点，写入如下代码，

float rad = chf('rad');         //圆锥底面半径
float height = chf('height');   //圆锥高度
int num = chi('num');           //圆锥底面点数int pts[] = array();
for(int i=0; i<num; i++){float ang = $PI * 2.0 / num * i;    //360°按点数均分int pt = addpoint(0, set(cos(ang), 0.0, sin(ang)) * rad);append(pts, pt);        //生成的点存到数组中
}
i[]@pts = pts;int cpt = addpoint(0, set(0, height, 0));   //圆锥高度//底面相邻的两个点与顶点相连
for(int i=0; i<len(pts); i++){int pt1 = pts[i];int pt2 = pts[(i+1) % len(pts)];    //取余数更保险int tri = addprim(0, 'poly', cpt, pt1, pt2);
}

结果：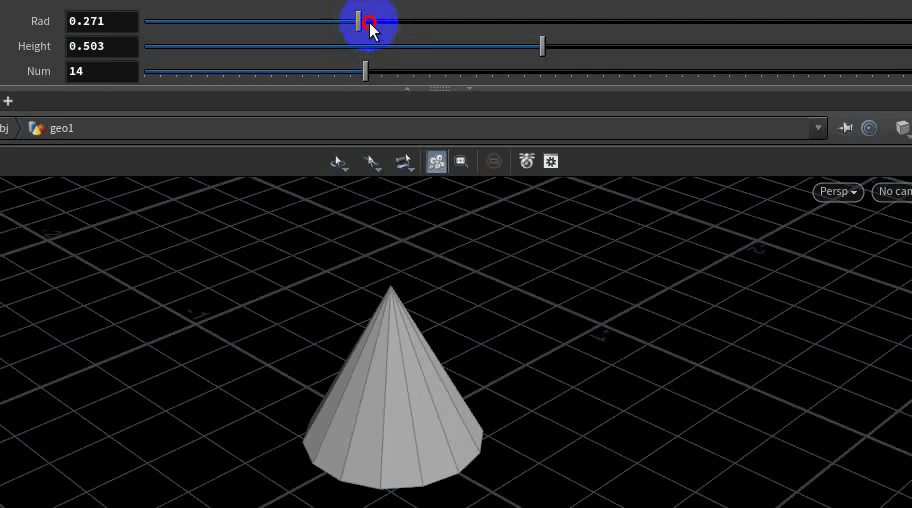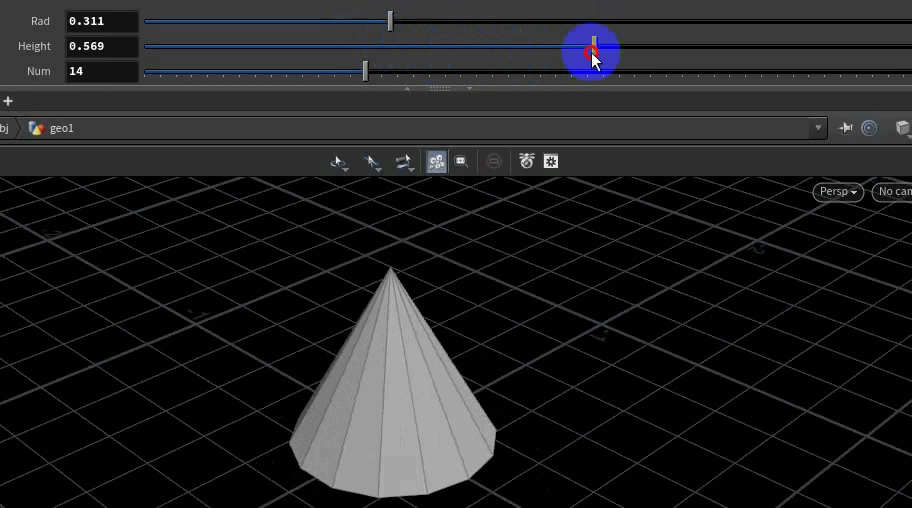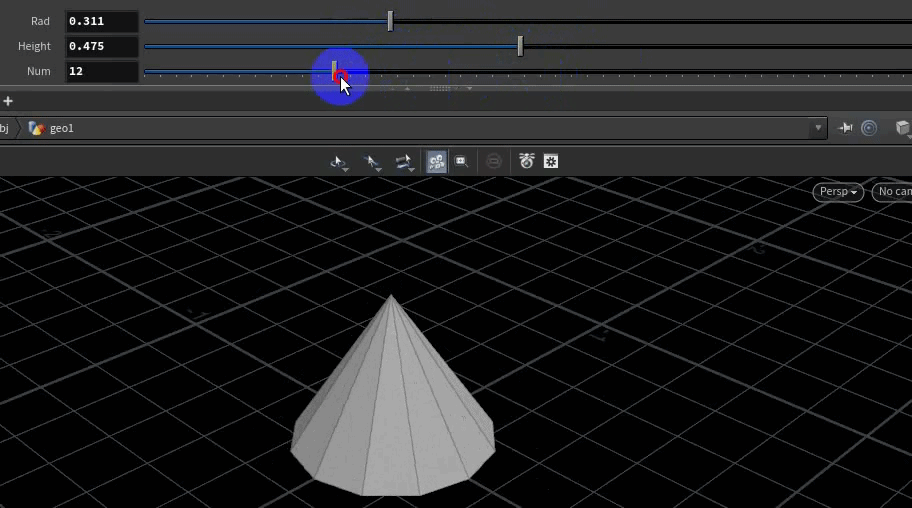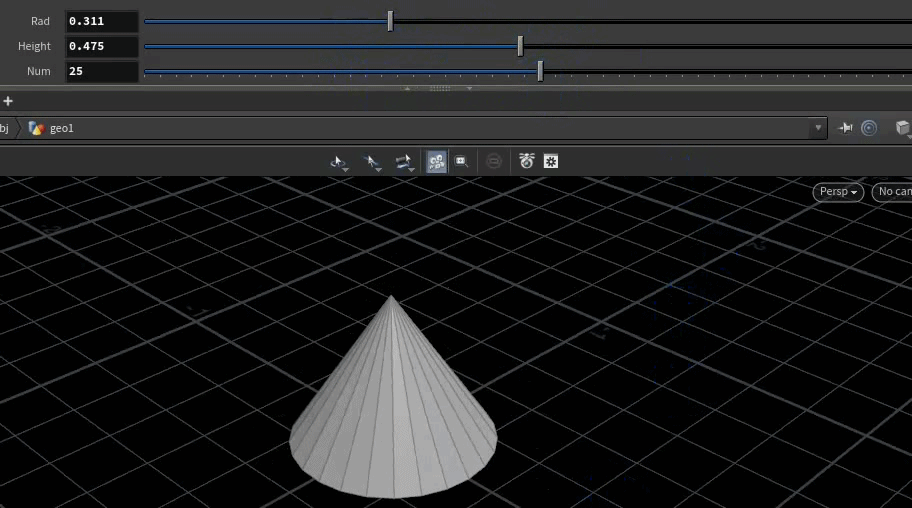

5、创建线

  eg.创建类型为Detail的AttributeWrangle节点，写入如下代码，

int pt1 = addpoint(0, set(-1.0, chf('h1'), 0.0));
int pt2 = addpoint(0, set(1.0, chf('h2'), 0.0));int polyline = addprim(0, 'polyline', pt1, pt2);

结果：略

6、螺旋形折线

与【2、Create Sprial Points创建螺旋点】类似，可使用 addvertex() 函数 或 addprim() 函数。

 eg.创建类型为Detail的AttributeWrangle节点，写入如下代码，

float ang = chf('ang') * $PI;   //角度值float steplen = chf('len');//方法一
//int sprialcrv = addprim(0, 'polyline');     //声明一个空折线对象//方法二
int pts[] = array();for(int i=0; i<chi('num'); i++){float x = cos(i * ang);     //x坐标float z = sin(i * ang);     //z坐标float y = i * 0.1;          //每次循环高度递增vector pos = set(x, y, z) * steplen;    //相当于缩放int pt = addpoint(0, pos);  //创建点//方法二append(pts, pt);//方法一//addvertex(0, sprialcrv, pt);        //添加顶点
} //方法二
int sprialcrv = addprim(0, 'polyline', pts);

结果：在 Ang=0.1，num=0.2，num=100 条件下，（为排版美观，图已旋转）

7、 删除点和面

eg.①创建一个Grid节点，细分设置20*20，
②创建类型为Points的AttributeWrangle节点，与Grid连接，

float rad = chf('d');
if(length(@P) < rad){removepoint(0, @ptnum);    //图一
}

③创建类型为Primitives的AttributeWrangle节点，与Grid连接，

float rad = chf('d');
if(length(@P) < rad){removeprim(0, @primnum, 1);     //图二removeprim(0, @primnum, 0);     //图三
}

结果为：当半径 d=0.5 时，

8、从面获取点

eg.给Box每个面开孔，如下图所示，

理论：
①获取每个面的四个顶点，
②面的中心点与面的每个顶点为方向，自定长度，可得出新顶点（挖孔面的点）的位置，
③面的顶点与新顶点，两两相连。
操作：
创建类型为Polygon的Box，添加并连接在类型为Primitives的AttributeWrangle节点，写入代码，

int pts[] = primpoints(0, @primnum);    //获取每个面的顶点i[]@pts = pts;                        //可写可不写
int npts[] = array();
for(int i=0; i<len(pts); i++){         //循环次数为每个面的顶点数int pt = pts[i];vector pos = point(0, 'P', pt);         //面中心点位置vector dir = (pos -@P) * chf('size');   //中心点与面顶点为方向 * 自定义长度vector newpos = @P +dir;                //新顶点位置int newpt = addpoint(0, newpos);        //创建点append(npts, newpt);                    //对新的4个顶点放入数组pts中
}for(int i=0; i<len(pts); i++){              int pt1 = pts[i];                       //面的顶点int pt2 = pts[(i+1) % len(pts)];int pt3 = npts[(i+1) % len(pts)];       //新的顶点int pt4 = npts[i];int poly = addprim(0, 'poly', pt1, pt2, pt3, pt4);  //面顶点与新顶点两两相连
}removeprim(0, @primnum, 1);     //删除面，不保留点
//结果略

9、Primitives From Points从点获取面

pointprims() 函数，返回一个数组，返回包含该点的面。

eg.获取包含该点@ptnum的面，这些面的中心点与该点@ptnum依次连接，如下，

 操作：

创建类型为Polygon的Box，添加并连接在类型为Points的AttributeWrangle节点，写入代码，

int prims[] = pointprims(0, @ptnum);    //包含该点的面/图元i[]@prims = prims;int pts[] = array();
for(int i=0; i<len(prims); i++){        //包含该点的面有3个，所以循环3次int prim = prims[i];vector pos = prim(0, 'P', prim);    //在这3个面的中心位置创建点，有3个点int pt = addpoint(0, pos);append(pts, pt);removeprim(0, prim, 1);     //删除box的6个面，不保留点//在这里先删除，也不会影响其它点的运行
}for(int i=0; i<len(pts); i++){      //每2个面的中间点与点@ptnum相连int pt1 = pts[i];int pt2 = pts[(i+1) % len(pts)];int pt3 = @ptnum;int poly = addprim(0, 'poly', pt1, pt2, pt3);
}

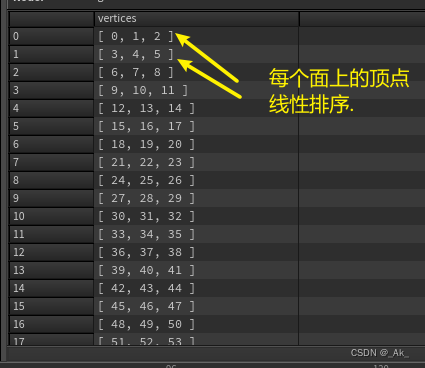
10、Vertex顶点排序

强烈推荐【以下内容大多摘自：知乎@刘鹏云——houdini 中的几何体函数2】

上一节案例创建了一个奇奇怪怪的菱形，它的法线并不全都是朝外，所以本节把它改正。

理论：
①利用点积判断面的朝向/法线，图片来自@知乎刘鹏云，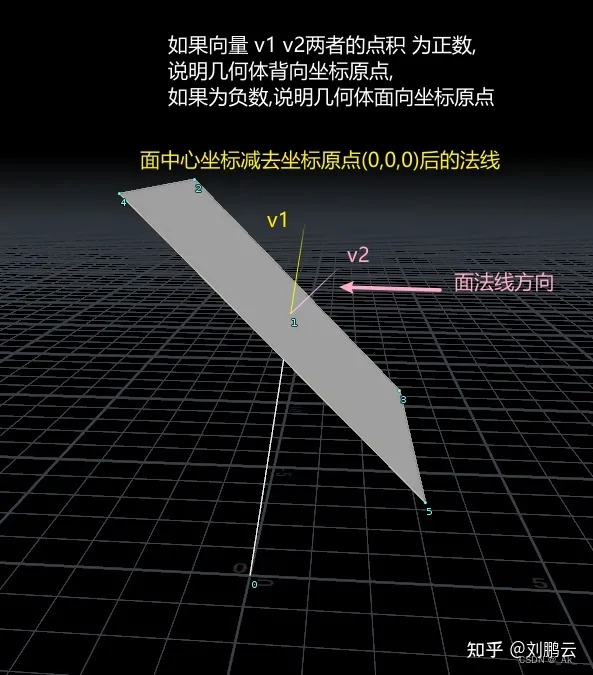

②反转顶点的顺序来实现面法线反转。
场景中打开顶点、面、面法线(添加类型为Primitives的Normal节点)、表格Vertices，观察可知，面法线与顶点的顺序有关：左手定则——>握拳方向和顶点排序方向保持一致,拇指方向即是面法线方向。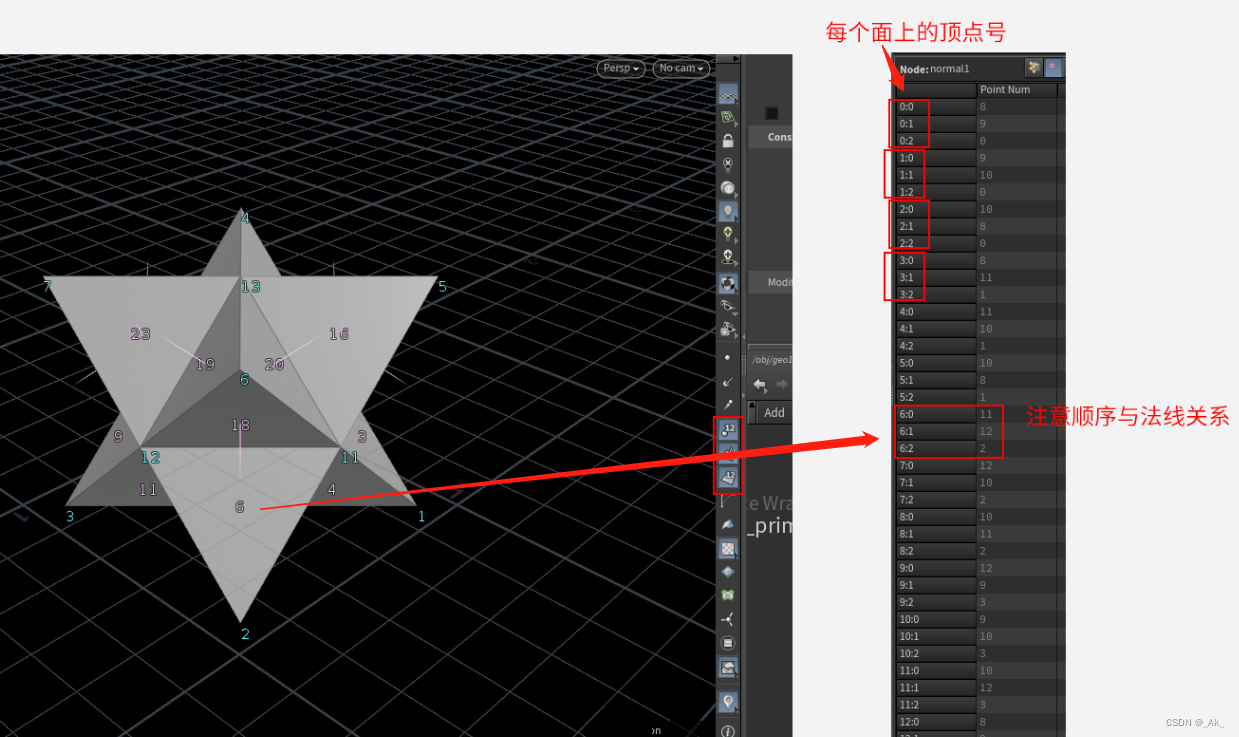

 操作：
①继续使用【9、Primitives From Points从点获取面】的案例，
②添加 fuse节点(融并相同点)、类型为Primitives的法线normal节点，
③添加类型为Primitives的AttributeWrangle节点，
④对上述节点依次相连，并在最后的节点写入以下代码，

vector dir = normalize(@P);     //原点到面中心点的向量值
float dotval = dot(dir, @N);    //点积<0，法线朝内
if(dotval<0){int vts[] = primvertices(0, @primnum);      //该面的所有顶点int pts[] = array();for(int i=0; i<len(vts); i++){              //顶点所在的点pointint vt = vts[i];int pt = vertexpoint(0, vt);append(pts, pt);}pts = reverse(pts);         //顶点组反排序，也可以在下面的循环条件内改为 i--for(int i=0; i<len(pts); i++){int pt = pts[i];int vt = vts[i];//setprimvertex(0, -1, vt, pt);setprimvertex(0, @primnum, i, pt);      //对顶点进行重排序，此函数记得去看@刘鹏云的文章}
}

 结果：略

关于 setprimvertex() 函数解析：图片来自知乎@刘鹏云

顶点的序号在geometry spreadsheet 的显示排列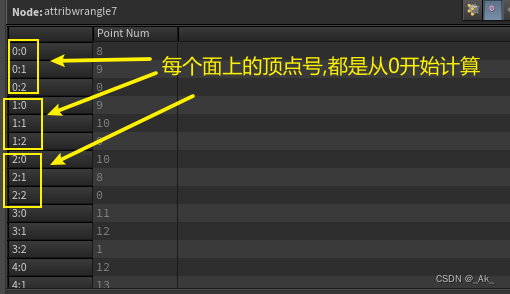

 而primvertices 返回的顶点号排序是线性的,每个顶点号都具有一个确切的数字.

11、最近点

eg.按下图创建节点，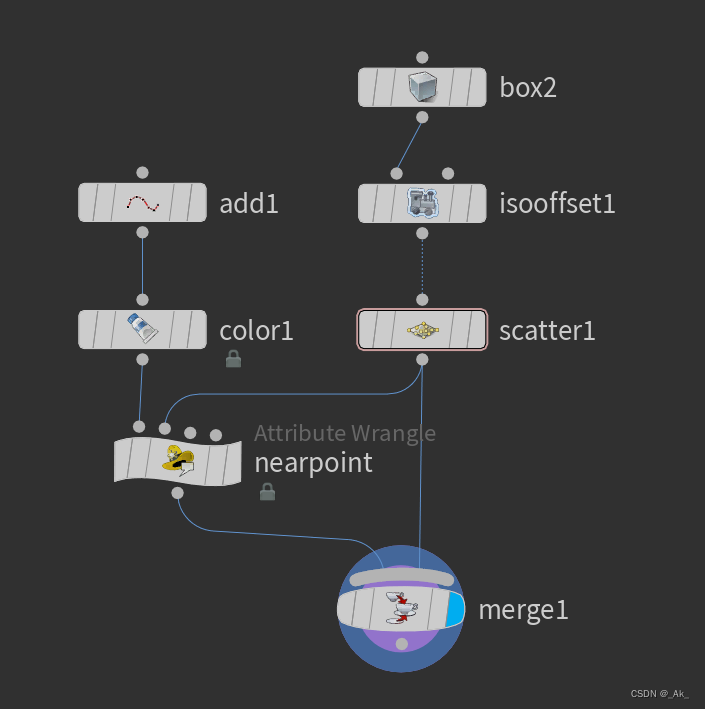

一些必要或非必要设置：
box2类型设为Polygon；
isooffset1采样设为50或随意：
add节点添加一个点，color节点可要可不要；
nearpoint类型为Points，写入代码，

int npt = nearpoint(1, @P);vector npos = point(1, 'P', npt);
int newpt = addpoint(0, npos);int line = addprim(0, 'polyline', @ptnum, newpt);

 结果为：图片来自知乎@刘鹏云，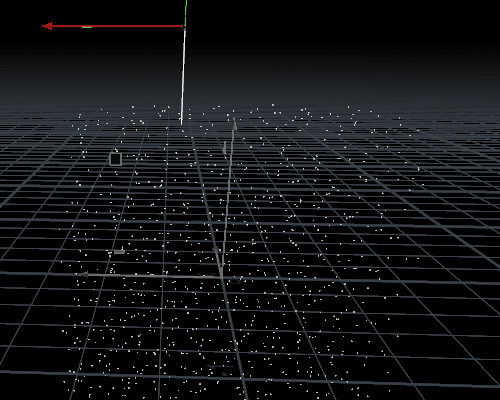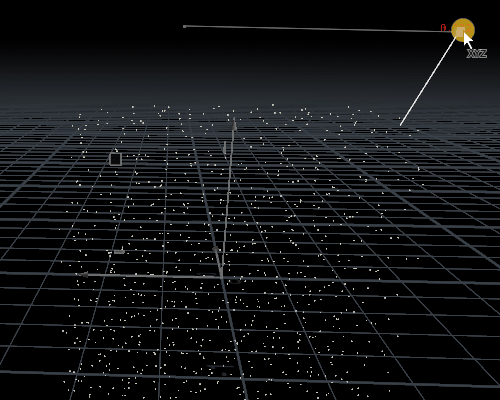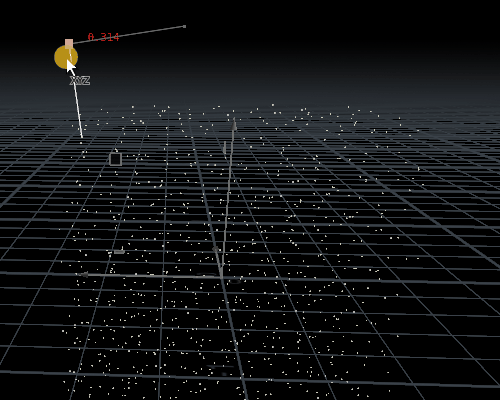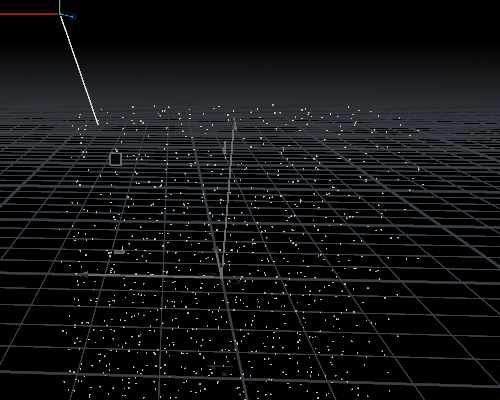

12、最近点们

eg.直接使用【11、Line with Nearpoints最近点】的案例，代码修改为：

int npts[] = nearpoints(1, @P, chf('dist'));i[]@npts = npts;for(int i=0; i<len(npts); i++){int npt = npts[i];vector npos = point(1, 'P', npt);int newpt = addpoint(0, npos);int line = addprim(0, 'polyline', newpt, @ptnum);
}

 结果：更改距离及点位置，图片来自知乎@刘鹏云，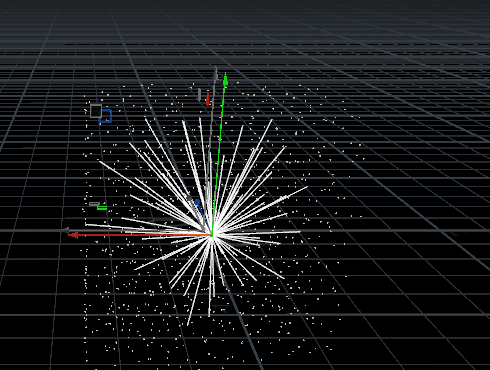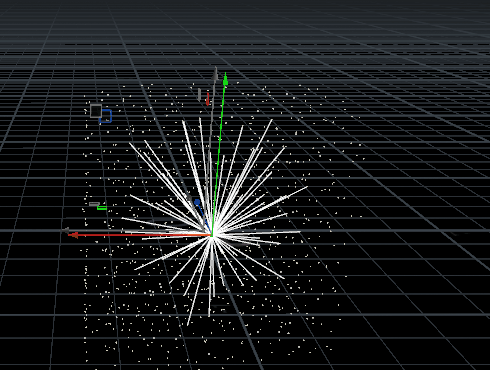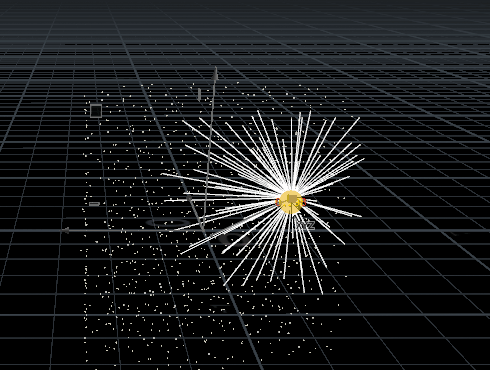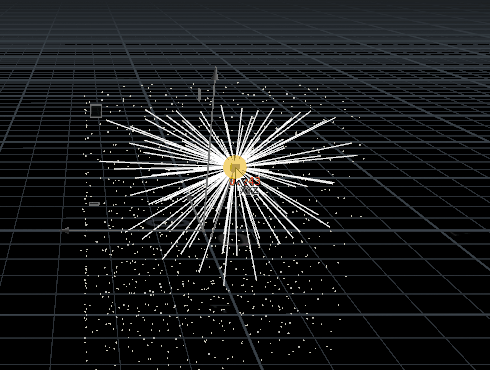

13、最近点与相连

eg.继续使用【11、Line with Nearpoints最近点】的案例，删除部分节点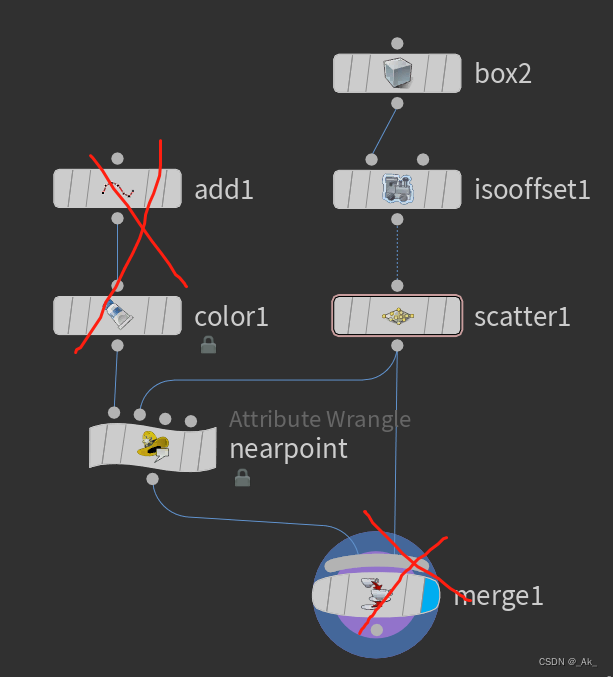

代码节点修改为：

int npts[] = nearpoints(0, @P, chf('dis'));     //最近点     搜索当前点的最近点，搜索范围:disfor(int i=0; i<len(npts); i++){int npt = npts[i];if(@ptnum < npt){   //避免重复相连int line = addprim(0, 'polyline', npt, @ptnum);}
}

 结果为：滑动dis值，图片来自知乎@刘鹏云，

14、几何体最近点

minpos() 函数：给一个位置，在几何体上找出对应最近的点。

本次案例大概是要做这么一个东西：

 操作：
如上右图，创建类型为Point的AttributeWrangle节点代替ray1节点，并写入如下下代码，
小球类型polygon，细分、大小看着设，

vector mpos = minpos(1, @P);@P = mpos;//结果：如上右图

15、柱体与螺旋线最近点

eg.一大一小的圆柱，中间放一根螺旋线，寻找螺旋线对应的最近点，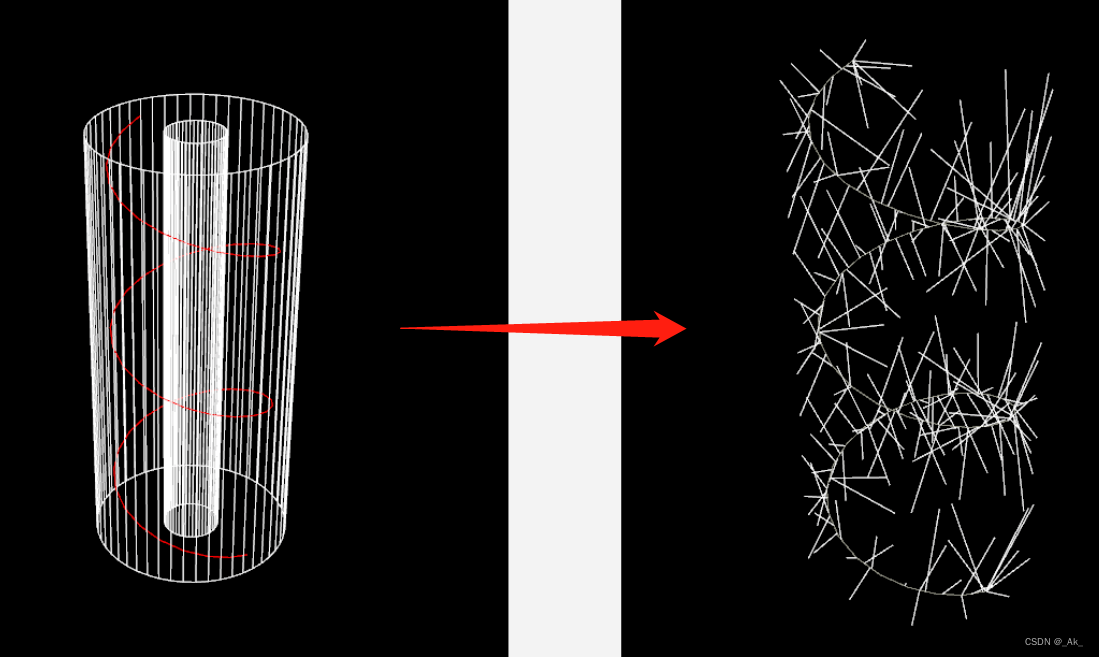

操作：
①按下图添加节点：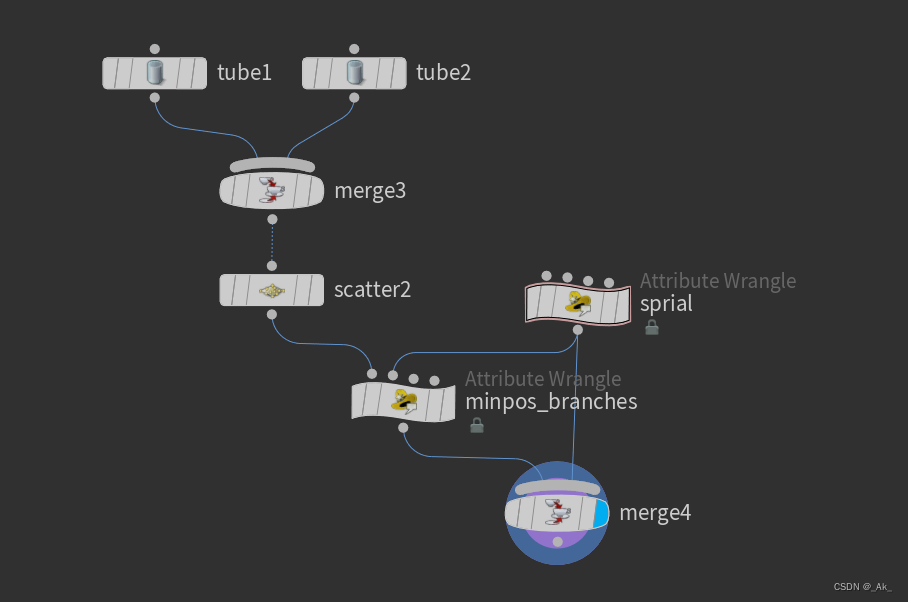

②一些设置：
a)sprial节点的代码使用【6、Create Sprial Polyline螺旋形折线】案例的代码，
b)tube1、tube2都是Polygon类型，它们的高度、大小与sprial节点的通道进行绑定（也可以自由设定），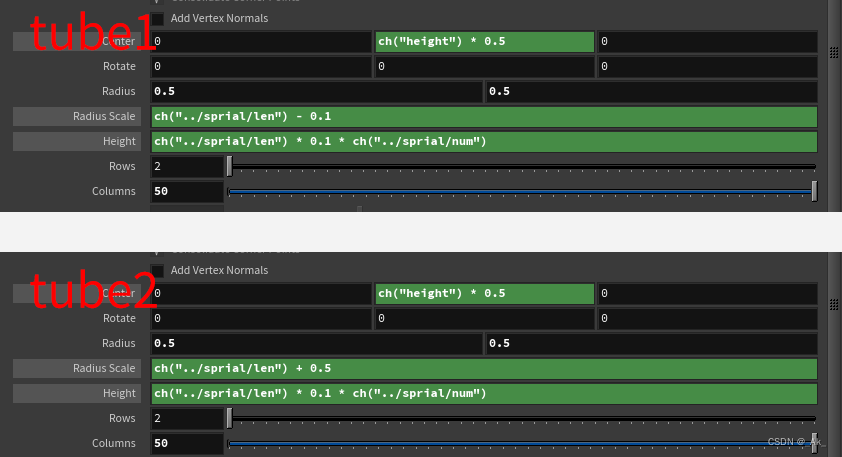

c)scatter2节点粒子数随意，
d)在类型为Points的minpos_branches节点中写入如下代码，

vector mpos = minpos(1, @P);
int mpt = addpoint(0, mpos);
int line = addprim(0, 'polyline', @ptnum, mpt);

结果：大概如开头的右图 ，感兴趣可以改变螺旋线通道值，查看不同的变化。

16、相交函数

intersect() 函数：返回第一个相交点位置、UV值，若值为-1，则没有相交点。

eg.先上结果，寻找直线与小球的相交点，下图使用红色小球代替相交点，（如果直线在小球内部，表示没有相交点），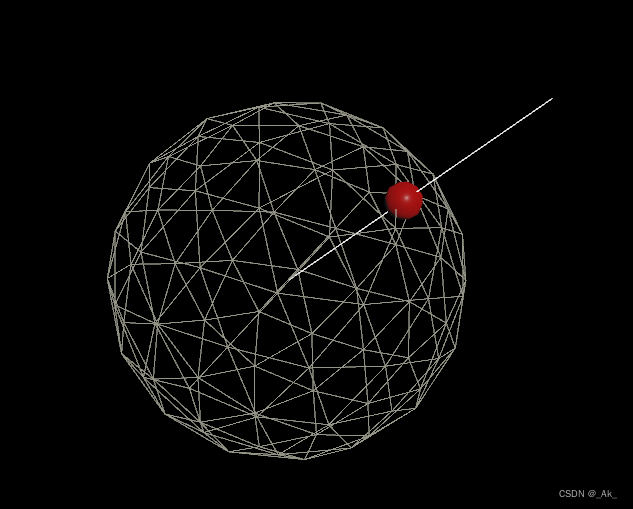

操作：
①按下图添加节点，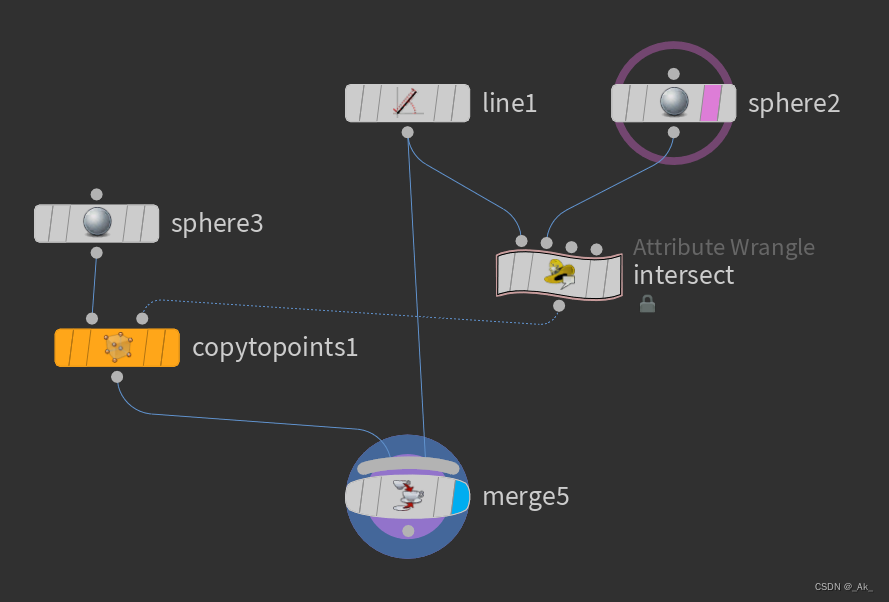

②一些设置，
a)两个小球Sphere类型可设置为Polygon，其中Sphere3可将其缩放，
b)copytopoints1节点的Target Points设置为interpt，
c)在类型为Primitives的intersect节点写入如下代码，

vector pos1 = point(0, 'P', 0);
vector pos2 = point(0, 'P', 1);
vector dir = pos2 - pos1;       //直线的长度及方向vector p, uv;
int interprim = intersect(1, pos1, dir, p, uv); //直线与小球的相交点，interprim是相交点所在的面
i@interprim = interprim;if(interprim >= 0){             //如果无相交点，则interprim值为-1int npt = addpoint(0, p);setpointattrib(0, 'Cd', npt, set(1, 0, 0));setpointgroup(0, 'interpt', npt, 1);            //对该点设置属性，方便后面小球复制到这里来
}

17、相交与投影

利用相交函数，本次做一个立方体在地面上的投影。

eg.先上结果：图片来自知乎@刘鹏云，注意，调整直线方向时，必须使其余地面有相交点，否则…

理论：以矩形的顶点为起始点 + 直线为方向(归一化)及自定义长度，然后与地面相交，
操作：
①按下图添加节点：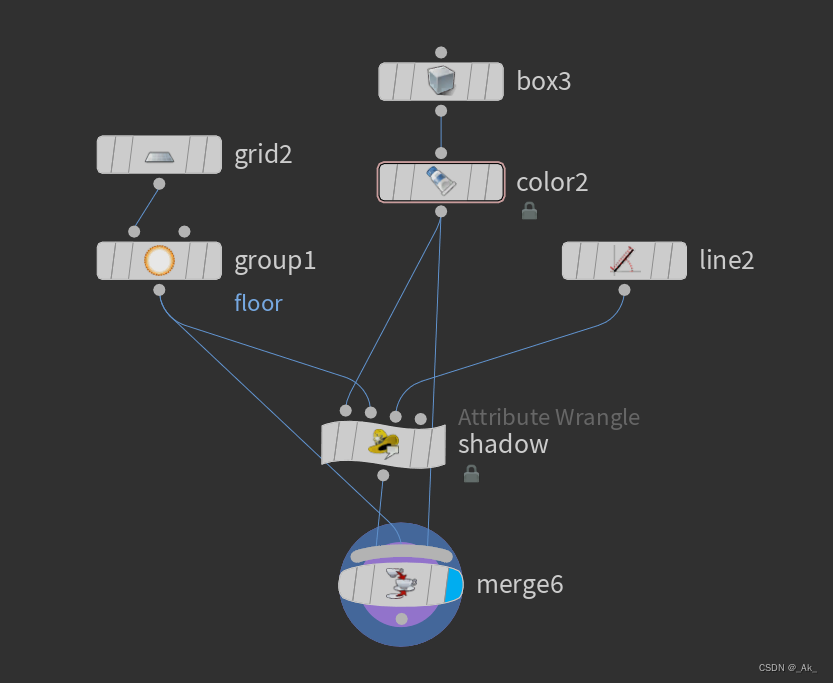
②一些设置：
a)grid2节点大小随意，类型为Polygon，
b)group1节点命名为floor，
c)box3节点中心点Y值设为1，类型为Polygon，
d)color2节点颜色随意，
e)类型为Points的shadow节点写入如下代码，

vector lpos1 = point(2, 'P', 0);
vector lpos2 = point(2, 'P', 1);
vector ldir = normalize(lpos1 - lpos2) * 1000;      //直线方向+自定义长度vector p, uv;
int interprim = intersect(1, 'floor', @P, ldir, p, uv); //矩形顶点——>直线方向+自定义长度，其其余地面的相交点
i@interprim = interprim;@P = p + set(0, 0.001, 0);      //矩形的点映射到相交点，不加0.001，影子会与地板重叠
@Cd = set(0, 0, 0);             //黑色"影子"

18、多边形相邻点

先上结果，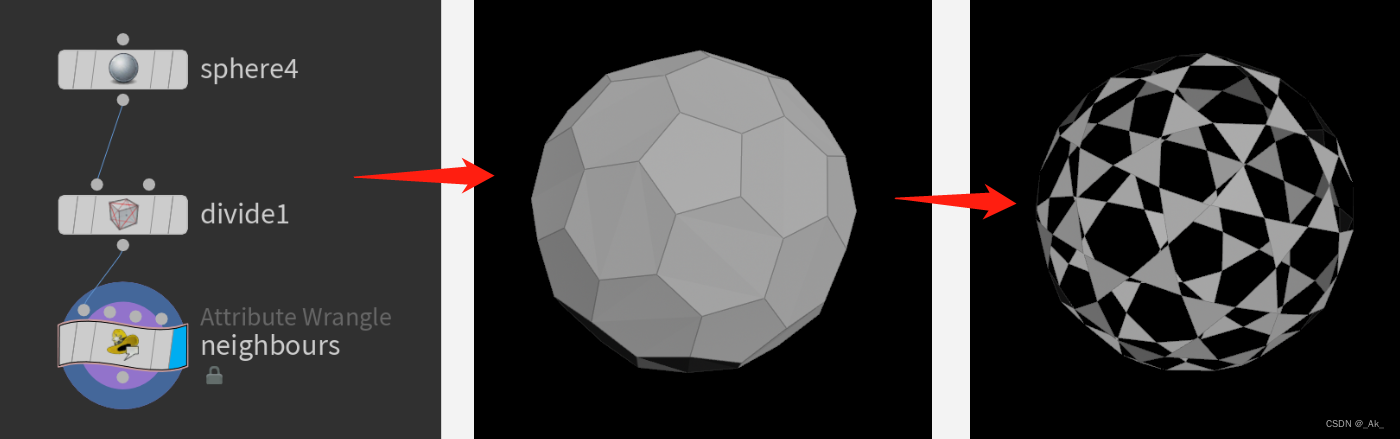

操作及设置：
按上右图添加节点，并进行设置，
a)sphere4节点类型为polygon，
b)divide1节点勾选 Compute Dual，即把多边形变成偶数点/边，
c)在类型为Points的neighbours节点写入如下代码，

int neighs[] = neighbours(0, @ptnum);       //与该顶点相连的点int poly = addprim(0, 'poly');
for(int i=0; i<len(neighs); i++){int neigh = neighs[i];vector npos = point(0, 'P', neigh);vector dir = npos - @P;                    //顶点与相邻点之间为方向vector newpos = @P + dir * chf('rad');    int newpt = addpoint(0, newpos);        //顶点与相邻点的之间位置创建一个新点addvertex(0, poly, newpt);              //三点成面，即三角形
}removepoint(0, @ptnum);     //删除小球的点

结果：图片来自知乎@刘鹏云，

19、随机取点的相邻点及相连接

 在模型上随机选点，该点的相邻点连成线。

先上结果：线框显示模式下，随机seed值为随机，

理论：
随机在模型上取点，该点的相邻点构成线，
连线之前，判断【该点的相邻点】是否已经使用过，
未使用过，则继续使用【该点的相邻点】的【相邻点】，以此循环。
操作：
①按上图添加节点，
②一些设置：
a)remesh节点的Target Size设为0.1或随意。它的作用是使用(近似等边)三角形重新创建输入曲面的形状，
b)在类型为Detail的attributeWrangle节点写入如下代码，

int conns[] = array();      //该数组用作保存已使用过(已连接)的点for(int t=0; t<1000; t++){int pt = npoints(1) * rand(chf('seed') + 5.25 * t);     //获取随机点pt，rand()函数随机返回0~1if(find(conns, pt) < 0){                        //若该随机点没有使用过，则执行循环int polyline = addprim(0, 'polyline');      //创建一个空折线，后续添加点，连成线//循环创建多个点连成多段线for(int i=0; i<1000; i++){append(conns, pt);                      //把该点加入数组conns，即标记为已使用vector pos = point(1, 'P', pt);         //随机点pt的位置int newpt = addpoint(0, pos);           //在随机点的位置创建新的点vector col = rand(2.651 * t + chf('seed')); //创建一个随机值，下面用作创建随机颜色setpointattrib(0, 'Cd', newpt, col);    //随机颜色addvertex(0, polyline, newpt);          //在随机点创建的点，添加到折线中去int npts[] = neighbours(1, pt);         //随机点的相邻点int check = 0; //检查相邻点们有没有使用过，未使用过，则该点用作下一个点for(int n=0; n<len(npts); n++){         int npt = npts[n];if(find(conns, npt) < 0){           //相邻点未使用过，执行if内代码pt = npt;                       //未使用过的点，作为下一个"随机点"check = 1;break;}}if(check == 0){break;}}}
}