本文主要是介绍深入探索STARK的安全性和可靠性——STARKs全面安全分析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1. 引言
- non-interactive STARKs,起源于Interactive Oracle Proofs (IOPs),然后通过random oracle模式转换为非交互式。
- StarkWare团队 ethSTARK Documentation – Version 1.2(2023年7月)论文做了更新,给出了完整具体的random oracle模式下的ethSTARK安全性分析。本文对该论文的更新做了解释。
2. STARK安全性解释
STARK proof system (Scalable Transparent Argument of Knowledge)是用于证明计算完整性(CI,computational integrity)的强大工具:
- 支持以trustless方式,来验证基于某公开数据的计算的正确性。
本文深入探索由STARK proofs所提供的安全性,对该安全性进行定义,并探索证明方案安全性的技术。
详情见:
- StarkWare团队 ethSTARK Documentation – Version 1.2(2023年7月)论文第6章。
- Justin Thaler等人2023年论文Fiat-Shamir Security of FRI and Related SNARKs。
我们试图通过安全分析实现什么?:
- 试图找到一种对STARK系统的“成功攻击”方式,使得对于某false statement,可生成让STARK Verifier 接受的 STARK proof。
由于false statement是危险的,可能具有任意大小和形状,而所构建的STARK系统是希望能抵御 所有 false statement的。
任何false statement,哪怕是1+1=3,若可基于该false statement生成让STARK Verifier信服的STARK proof,则可认为是对该STARK系统的成功攻击。(有密码学背景的人可能会对,STARK所满足的更强安全概念——“knowledge soundness”,感兴趣。为简化表述,本文关注更简单的soundness。“knowledge soundness”知识具体可参见Eli Ben-Sasson等人2016年论文 Interactive Oracle Proofs。)
如何来正式定义某STARK系统的安全性呢?:
- 通过粗略计算,攻击者构建成功攻击所需的“cost(开销)”,来分析“soundness error”。即,找到某能让STARK Verifier接受的 false statement的 STARK proof。
- 从数学上说,“soundness error”对应为某函数 ( t ) (t) (t):
- 其输入为时间参数“ t t t”,代表攻击者发起攻击所需的计算时长。
- 其输出为攻击者攻击成功的概率。所谓攻击成功,是指找到了某false statement让人信服的proof。
- 若攻击者愿意花费的“cost(开销)” t t t越大,则其攻击成功的概率将增加。
为此,可将STARK安全性定义为函数 ( t ) (t) (t):
- 其不同于在crypto Twitter上讨论安全性的自然方式。
如,对于“本方案具有96位安全性”这样的陈述,如何将其转换为安全性定义?
答案是不唯一的,因为人们对“ x x x-位安全性”的理解有细微差异:
- 1)版本1:严格意义上来说:是指,对于任意的 t ∈ [ 1 , 2 96 ] t\in[1,2^{96}] t∈[1,296],该soundness error为 ( t ) 2 96 (t)2^{96} (t)296。即,对于任意运行时长最多为 2 96 2^{96} 296的攻击者,其成功的概率很小,小于 2 96 2^{96} 296——即小于 “10亿✖️10亿✖️10亿”。
- 2)版本2:宽松意义上来说(或是更通用版本): 96 96 96-位安全性,是指对于任意的 t t t,对 t / ( t ) 2 96 t/(t) 2^{96} t/(t)296其成立。即意味着,成功概率与运行时长呈(inverse)线性关系。如,某攻击者的运行时长为 2 86 2^{86} 286,则其成功的概率最多为 2 10 2^{10} 210。
本文基于上面的版本2来分析。
3. 由IOPs 到 具有96-位安全性的STARKs
如何来证明某方案具有96位安全性呢?
需先理解如何构建STARKs的高层结构。
STARK主要有3大要素:
- 1)an IOP(interactive oracle proof)
- 2)a Merkle tree
- 3)a Fiat-Shamir hash
一旦定义了这3大要素,就可将其编译生成某STARK
本文主要关注IOP。同时将详细说明这3大要素,以及如何将它们组合在一起。
3.1 IOP
IOP类似于表中的interactive proof,其中某Prover和Verifier多轮交互。(本文限定为public-coin协议,即Verifier仅需给Prover发送random challenges)。
在IOP中,Verifier不读取完整的Prover消息,而是仅从每个Prover消息中采样少量bits。从而可实现后续编译出的STARK的简洁性。
3.2 由IOP到STARK
有IOP之后,如何基于该IOP构建某STARK呢?
- Prover消息可能很长(事实上,其要长于计算本身)。
- 为压缩消息,会使用Merkle tree。
- Merkle tree是二进制哈希tree,每个叶子节点代表IOP的某query或某answer。
- Merkle tree root为对整个消息的承诺值。
- 当Verifier想要读取该消息的某特定位置时,Prover会提供该位置的值以及相应的认证路径。Verifier可使用该路径来验证该值的正确性。
- IOP Verifier仅需读取Prover消息的少量位置。从而使用Merkle tree构建了succinct且具有少量通讯的协议。
4. Compressing Rounds
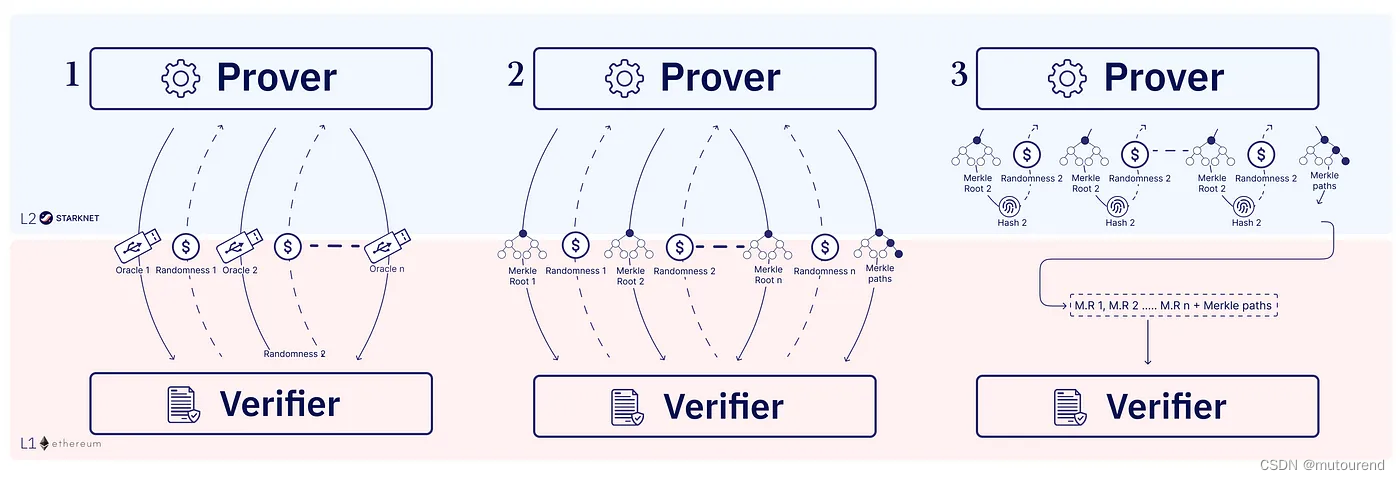
对于交互式STARK,为简化流程,通常会将其转换为非交互式的,这样在构建时Prover就无需再等待外部消息。事实上,当前所部署的所有STARK系统,包括ethSTARK协议,都是非交互式STARK。
非交互式STARK也是transparent SNARKs的一个特例(所谓transparent,是指在实例化时无需trusted setup,又名“Arthur Merlin protocol”或“public coin IOP”)。最终,最后一步是应用Fiat-Shamir来将rounds压缩为单个消息,称其为STARK proof。
Fiat-Shamir转换会将交互式协议转换为非交互式协议:
- Prover 通过“talking to a hash function”来模拟交互协议。为派生第 i i i轮的随机挑战值,Prover需对直到第 i i i轮的所有transcripts都进行哈希,将相应的哈希输出结果作为下一挑战值。
这样可确保Prover在生成挑战值之后无法改变其responses。
然而cheating Prover有一些新的(交互式IOP所没有的)策略手段。cheating Prover可通过修改最后一条Prover消息(这将给出新的transcript,从而给出新的挑战值),来重新生成Verifier挑战值。由此可知,IOP的标准可靠性概念不足以证明Fiat-Shamir转换的安全性。
如,考虑一个有96轮的IOP,对Verifier进行如下“hack”:
- 若96轮中,Verifier的每个随机值的第一位是0,在该Verifier接受(而根本不看proof)。
一旦对Verifier添加了该hack,其仅给IOP的soundness error加了一项 2 96 2^{96} 296。但是,经Fiat-Shamir转换之后,攻击者很容易通过修改Prover消息,来确保每个哈希结果以0开头,从而在很短时间内破解该系统。
不过请放心,这仅仅是个理论示例,而不适用于已部署的STARK。
为何StarkWare的STARK是安全的呢?
简而言之,将展示最多允许 n n n步的攻击者,其攻击成功的概率最多为 ( t ) t 2 96 (t)t 2^{96} (t)t296。
4.1 IOPs and Round-by-Round Soundness
STARK仅可与其底层的IOP一样安全。但是,某IOP具有96位安全性,意味着什么?
标准定义应是:该IOP的soundness error为 2 96 2^{96} 296,即意味着,任何攻击者(不考虑运行时长)愚弄Verifier的概率最多为 2 − 96 2^{-96} 2−96。
但是,正如之前所讨论,STARK由3大要素组成,IOP soundness只是三者之一,其并不足以让由三大要素所编译的STARK也具有96位安全性。
事实上,所编译的STARK的安全性证明,是假定该STARK具有96位 round-by-round soundness error(有时,也称为state-restoration soundness)。
直观来说,round-by-round soundness error是指:
- 每轮的安全性为96位,而不仅是整体协议的安全性是96位。
更具体来说,round-by-round是指:
- 存在某predicate,已知该协议的某partial transcript,可告知该transcript是否是“fooling”的。
- empty transcript不是“fooling的”。
- 当且仅当Verifier接受,某full transcript是“fooling”的。
- 对于任何不愚弄Verifier的partial transcript,在下一轮中该transcript是“fooling”的概率最多为 2 96 2^{96} 296。
- 若存在满足以上属性的predicate,则称该协议具有96位round-by-round soundness(不要求该predicate可高效计算)。
很多情况下,仅分析了某IOP的soundness,而未分析其round-by-round soundness。
需承认的是,很难想到一个例子——某IOP具有标准可靠性,但不是round-by-round soundness(人为例子除外)。
但是IOP soundness与round-by-round soundness 是有差别的:
- 当派生具体的安全上限时,每个bit都是有关系的。
- 为此,为派生严谨具体的上限时,必须对IOP的round-by-round soundness 进行严谨分析。StarkWare团队对FRI协议以及ethSTARK IOP均做了相应的严谨分析。该分析自身不在本文详述。
- 具体见2023年2月视频StarkWare Sessions 23 | The Soundness of FRI | Dan Carmon
- 借助新的分析,可为StarkWare的STARK proof设置精确的参数。
round-by-round soundness 可给出所需的保证:
- Prover可多次重新生成挑战值,但是对于任意round,其生成“fooling” transcript的概率为 2 96 2^{96} 296。
因此,若该Prover具有time t t t——用于衡量哈希调用次数,则其最多可尝试 t t t次来试图获得某“fooling” transcript,从而限制其成功概率为 ( t ) t 2 96 (t) t 2^{96} (t)t296。
5. Adding All the Error Terms
最后,需确保Prover无法对Merkle tree进行攻击。只需要构建Merkle tree所使用的哈希函数不存在碰撞即可。
攻击者对某随机函数调用 t t t次,尝试找到某碰撞的概率,最多为 t 2 / 2 t2/2 t2/2。其中 t 2 t2 t2为该哈希函数的输出长度(基于“生日悖论”)。这也是为何需设置哈希函数的输出长度,应为所需安全性的2倍。
若有某哈希函数的输出长度为192,且某IOP的round-by-round soundness为96位,则所编译的STARK的soundness error为 ( t ) = t 2 96 + t 2 ⋅ 2 196 (t)=t2^{96}+t2\cdot 2^{196} (t)=t296+t2⋅2196。最终该STARK方案的安全性为95位,因 t / ( t ) = t / ( t 2 96 + t 2 ⋅ 2 196 ) = 1 / 2 96 + 1 / 2 96 = 2 − 95 t/(t)=t/(t2^{96}+t2\cdot 2^{196})=1/2^{96}+1/2^{96}=2^{-95} t/(t)=t/(t296+t2⋅2196)=1/296+1/296=2−95。
6. 总结
STARK proof system (Scalable Transparent Argument of Knowledge)是用于证明计算完整性(CI,computational integrity)的强大工具:
- 支持以trustless方式,来验证基于某公开数据的计算的正确性。
STARKs的安全性通常以“soundness error”来衡量,其代表了攻击者成功为某false statement提供让Verifier信服的proof 的概率。
为实现所需的安全性,如96位,底层的IOP必须满足round-by-round soundness,以确保每轮都维护高级别安全性。
StarkWare团队分析了ethSTARK底层的round-by-round soundness,从而可派生出具体的安全上限。
参考资料
[1] StarkWare团队2023年10月博客 Safe and Sound — A Deep Dive into STARK Security
这篇关于深入探索STARK的安全性和可靠性——STARKs全面安全分析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





