在本系列的上一篇文章中，我们谈到了，如何能够做出一些非常有意思且简洁的计算证明，比如通过利用多项式复合和除法技术，证明你算出了第一百万个斐波那契数。但是，它依托于一个非常重要的元素：给定一个集合，里面有很多的点，你必须能够证明集合里的大部分点都在同一个低次多项式上（译者注：本文所译的多项式度数或次数，皆对应 degree 一词）。这个叫做“低次测试”的问题，可能是协议中最为复杂的部分。 首先，再

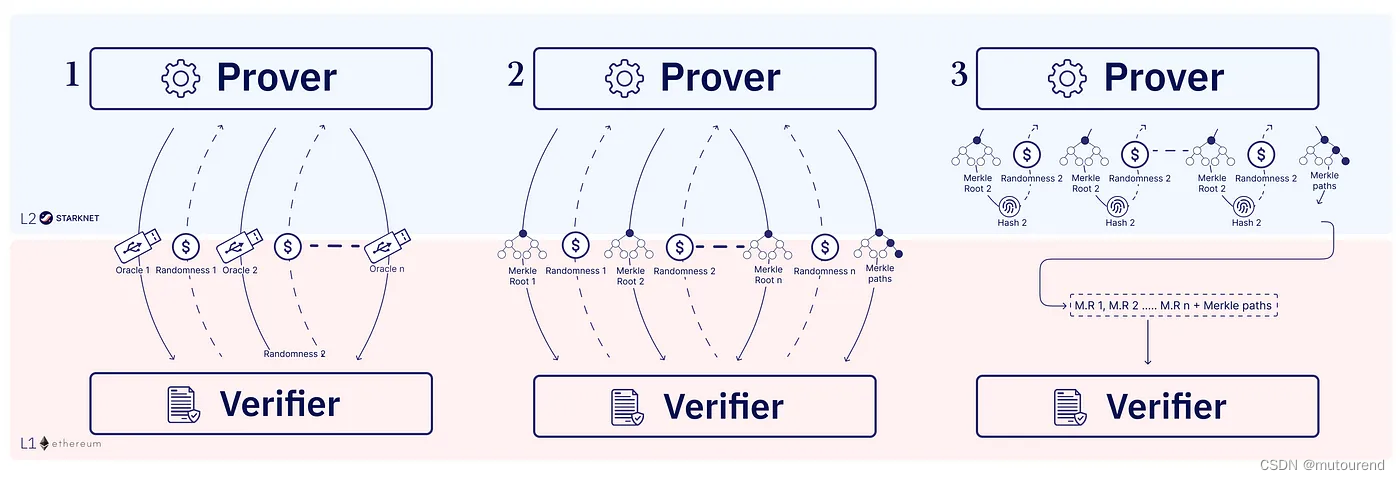
在本系列的上一篇文章中，我们谈到了，如何能够做出一些非常有意思且简洁的计算证明，比如通过利用多项式复合和除法技术，证明你算出了第一百万个斐波那契数。但是，它依托于一个非常重要的元素：给定一个集合，里面有很多的点，你必须能够证明集合里的大部分点都在同一个低次多项式上（译者注：本文所译的多项式度数或次数，皆对应 degree 一词）。这个叫做“低次测试”的问题，可能是协议中最为复杂的部分。 首先，再

STARKs 系列： 干货 | STARKs, Part I: 多项式证明干货 | STARKs, Part II 特别感谢 Eli ben Sasson 一如既往地提供帮助；也特别感谢 Chih-Cheng Liang和Justin Drake 的审阅。 为本系列的第 1 部分和第 2 部分的后续内容，本文将介绍在实际中实现 STARK 的途径与效果，并使用 python 语言进行实现

1. 引言 前序博客有： 2023年 ZK Hack以及ZK Summit 亮点记为何需关注各ZKP方案的benchmarks？ 很久以前，有大量研究和开发致力于改进ZKP性能。研究人员通过采用多种不同的技术，包括但不限于： 不同的IOPs不同的多项式承诺方案不同的哈希函数不同的硬件加速，等 来不断优化： Prover timeVerifier time以及，Proof size。

1. 引言 non-interactive STARKs，起源于Interactive Oracle Proofs (IOPs)，然后通过random oracle模式转换为非交互式。StarkWare团队 ethSTARK Documentation – Version 1.2（2023年7月）论文做了更新，给出了完整具体的random oracle模式下的ethSTARK安全性分析。本文对该