本文主要是介绍HMM学习二:Baum-Welch算法详解(学习算法),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一,前言
在上篇博文中,我们学习了隐马尔可夫模型的概率计算问题,如果对隐马尔可夫模型还不胜了解的话,可参看博文HMM学习(一)。
学习问题
隐马尔可夫模型的学习,根据训练数据是包括观测序列和对应的状态序列还是只有观测序列,可以分别由监督学习与非监督学习实现。本节首先介绍监督学习算法,而后介绍非监督学习算法——Baum-Welch算法(也就是EM算法)。
监督学习问题
假设已给训练数据包含S个长度相同的观测序列和对应的状态序列 ( O 1 , I 1 ) , ( O 2 , I 2 ) , . . . , ( O S , I S ) ( O 1 , I 1 ) , ( O 2 , I 2 ) , . . . , ( O S , I S ) {(O_1,I_1),(O_2,I_2),...,(O_S,I_S)}{(O_1,I_1),(O_2,I_2),...,(O_S,I_S)} (O1,I1),(O2,I2),...,(OS,IS)(O1,I1),(O2,I2),...,(OS,IS),那么可以利用极大似然估计方法来估计隐马尔可夫模型的参数,具体方法如下。
1.转移概率 a i j a i j a_{ij}a_{ij} aijaij的估计
设样本中时刻t处于状态i时刻t+1转移到j的频数为 A i j A i j A_{ij}A_{ij} AijAij,那么状态转移概率为 a i j a_{ij} aij的估计是
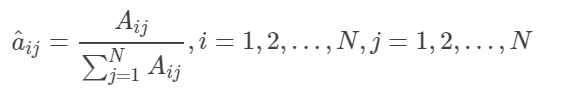
直接根据给定的O和I进行频数统计,在海藻模型中,我们可以统计100天前的天气转移次数,如在100天内,统计从sunny -> sunny 的次数,sunny -> cloudy 的次数,sunny - > rainy的次数,分别记作 a 1 , a 2 , a 3 a_1,a_2,a_3 a1,a2,a3,那么 a s u n n y − > a n y s t a t e a_{sunny−>any state} asunny−>anystate=[ a 1 a 1 + a 2 + a 3 \frac{a_1}{a_1+a_2+a_3} a1+a2+a3a1, a 2 a 1 + a 2 + a 3 \frac{a_2}{a_1+a_2+a_3} a1+a2+a3a2, a 3 a 1 + a 2 + a 3 ] \frac{a_3}{a_1+a_2+a_3]} a1+a2+a3]a3。因此,状态转移矩阵可以根据给定的隐藏序列 I I I计算得出。
2.观测概率
这篇关于HMM学习二:Baum-Welch算法详解(学习算法)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




