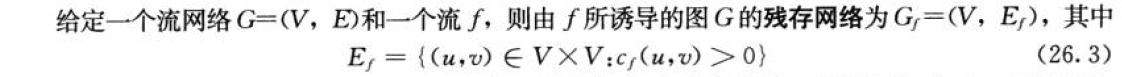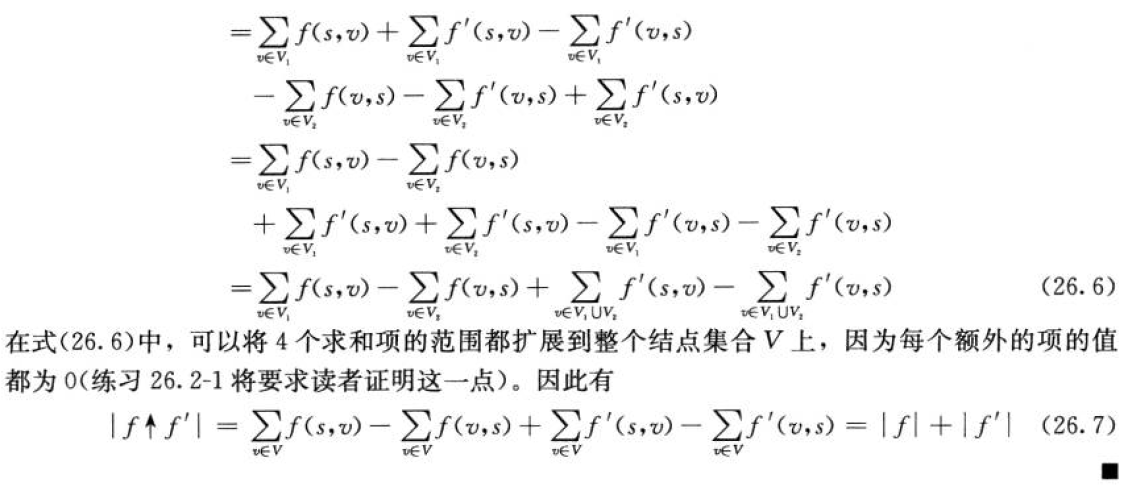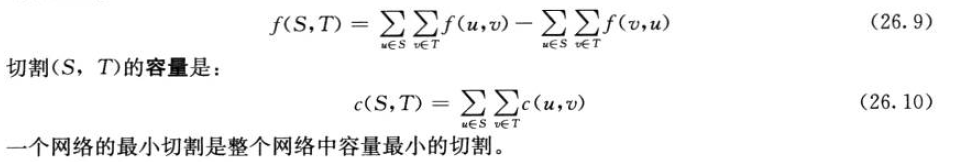算法导论 第二十六章 最大流

26.1 流网络

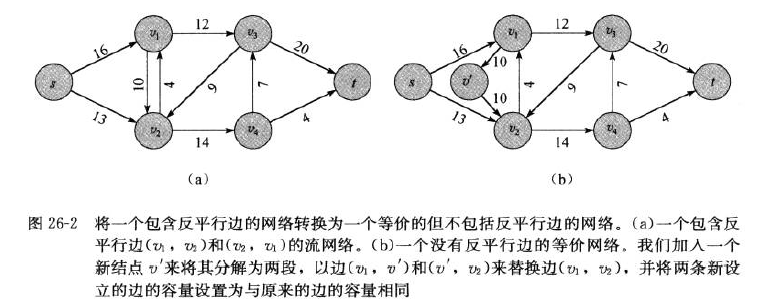
对于存在反平行边的问题，通过加入一个虚拟节点来保持性质，如对C(v1, v2) = a,C(v2, v1) = a，引入节点v'C(v1, v2) = a,C(v2, v') = a,C(v',v1) = a，如下图：

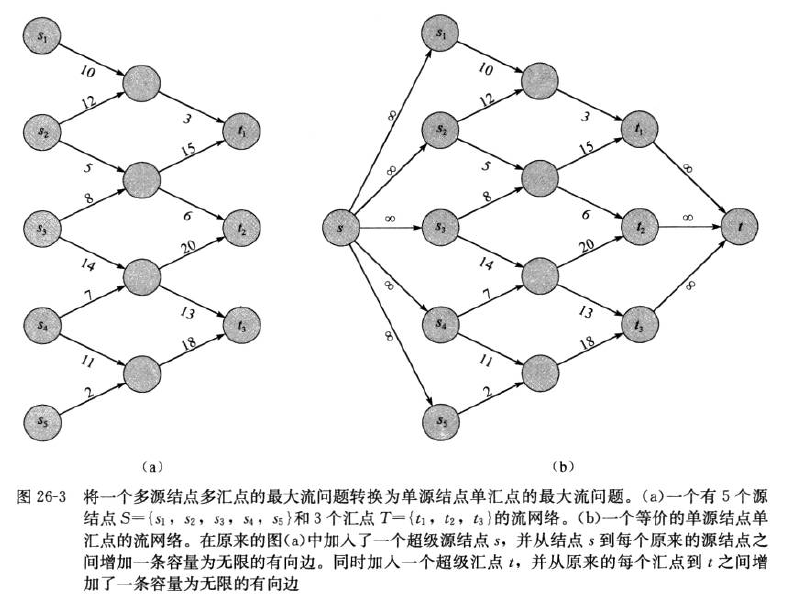
而对于多个源点和多个汇点的网络，通过引入一个超级原点和超级超级汇点来处理。

26.2 Ford-Fulkersion方法

def：残存网络为图的每条边还可以增加的流量。

就是在残存网络中找到一条由s到t的边，在原图中增加min(cf)是安全的，然后不断的增加知道残存网络中s再也无法到达t，就达到了流的最大值。实现如下：

def ENQUEUE(Q, s):  Q.append(s)  def DEQUEUE(Q):  r = Q.pop(0)  return rWHITE, GRAY, BLACK = (0, 1, 2)  
class Vertex:  def __init__(self, u):  self.value = uself.vertexs = []self.isInGraph = Falseself.pi = Noneself.color = WHITEself.index = Noneself.residual = []class Edge:  def __init__(self, u, v, c):  self.fromV = u  self.toV = vself.constraint = cclass Graph:def __init__(self):  self.vertexs = []self.constraint = Noneself.flow = Noneself.residual = Nonedef INITGRAPH(G, edges):for e in edges:if not e.fromV.isInGraph:e.fromV.index = len(G.vertexs)G.vertexs.append(e.fromV)e.fromV.isInGraph = Trueif not e.toV.isInGraph:e.toV.index = len(G.vertexs)G.vertexs.append(e.toV)e.toV.isInGraph = Truee.fromV.vertexs.append(e.toV)e.fromV.residual.append(e.toV)e.toV.residual.append(e.fromV)n = len(G.vertexs)G.constraint = [[0 for i in range(n)] for j in range(n)]G.flow = [[0 for i in range(n)] for j in range(n)]G.residual = [[0 for i in range(n)] for j in range(n)]for e in edges:G.constraint[e.fromV.index][e.toV.index] = e.constraintG.residual[e.fromV.index][e.toV.index] = e.constraintdef PRINT_GRAPH(G):for u in G.vertexs:print(u.value, u.index, ":")for v in u.vertexs:print(v.value, G.flow[u.index][v.index])print(G.residual)def RESIDUAL_BFS(G, s):  for v in G.vertexs:  if v != s:  v.color = WHITEv.pi = None  s.color = GRAYs.pi = None  Q = []ENQUEUE(Q, s)while len(Q) != 0:  u = DEQUEUE(Q)  for v in u.residual:if v.color == WHITE and G.residual[u.index][v.index] != 0:  v.color = GRAYv.pi = u  ENQUEUE(Q, v)  u.color = BLACKdef RESIDUAL_SHORTEST_PATH(G, s, t, path):RESIDUAL_BFS(G, s)if t.pi == None:return 0u, v = t.pi, tcf = float("inf")while u != None:path.append((u, v))cf = min(cf, G.residual[u.index][v.index])v = uu = v.piif path[-1][0] == s:path.reverse()print(cf)return cfreturn 0def PRINT_PATH(P):for v in P:if v.pi == None:print("|")print(v.value)def FORD_FULKERSON(G,s,t):#for e in G.edges:#    e.f = 0path = []cf = RESIDUAL_SHORTEST_PATH(G, s, t, path)while cf > 0:for (u, v) in path:print(u.value, v.value, cf, G.residual[v.index][u.index], G.residual[u.index][v.index])if G.constraint[u.index][v.index] > 0:G.flow[u.index][v.index] += cfG.residual[v.index][u.index] += cfG.residual[u.index][v.index] -= cfelse:G.flow[u.index][v.index] -= cfG.residual[v.index][u.index] -= cfG.residual[u.index][v.index] += cfprint(u.value, v.value, cf, G.residual[v.index][u.index], G.residual[u.index][v.index])path = []cf = RESIDUAL_SHORTEST_PATH(G, s, t, path)print("================")if __name__ == "__main__":s = Vertex('s')t = Vertex('t')v1 = Vertex('v1')v2 = Vertex('v2')v3 = Vertex('v3')v4 = Vertex('v4')edges = []edges.append(Edge(s, v1, 16))edges.append(Edge(s, v2, 13))edges.append(Edge(v1, v3, 12))edges.append(Edge(v2, v1, 4))edges.append(Edge(v2, v4, 14))edges.append(Edge(v3, v2, 9))edges.append(Edge(v3, t, 20))edges.append(Edge(v4, v3, 7))edges.append(Edge(v4, t, 4))G = Graph()  INITGRAPH(G, edges)#PRINT_GRAPH(G)#print("==============")FORD_FULKERSON(G, s, t)PRINT_GRAPH(G)

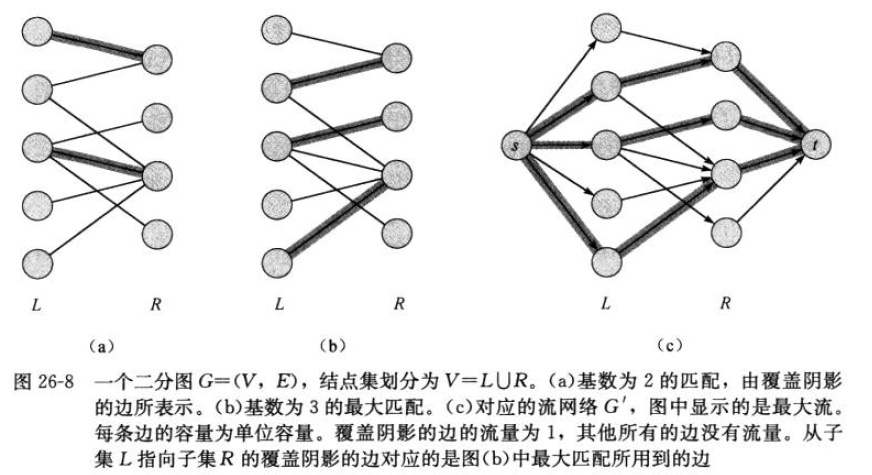
26.3 最大二分匹配

def：最大二分匹配问题：

则最大二分匹配容易转化为最大流问题：