纳什均衡:策略组合(组合是由每个博弈者的已选的策略构成,s1~sn)在N方博弈中,满足条件:如果对于每位博弈者i来说,选择都是Si是相对与其他博弈者所选策略S-i的最佳反应(BR),那么这个组合就是纳什均衡,用NE表示。
Motivations:(纳什均衡)
1.No regrets(无悔策略)--在给定其他人策略的条件下,每个博弈者都不会由于某种诱因而改变策略,即没有绝对的诱因使得博弈者改变策略。
2.self-fulfill beliefs(自我实现的信念)--
3.总有一些自然因素使得人们改变选择策略
Game One
有两个玩家进行博弈,选择和收益如下图所示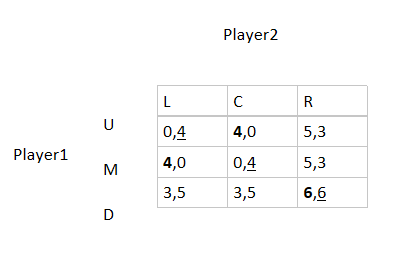
如何找到纳什均衡?找到彼此的BR
首先找到对于Playe1的BR是什么?
可知:
BR1(L)=M BR2(U)=L
BR1(C)=U BR2(M )=C
BR1(R)=D BR2(D)=R
值得一提的是,1号博弈者的每个策略对于某策略来说是最佳策略,同理适用于2号博弈者
此时NE = (D,R)
因为此时Player1对Player2做出了最佳对策,同时Player2对Player1也做出了最佳对策。
但是一个完全理性的1号博弈者可能会选择“M”,因为他们认为2号博弈者会选择“L”.
WHY?..........对话循环
Game Two
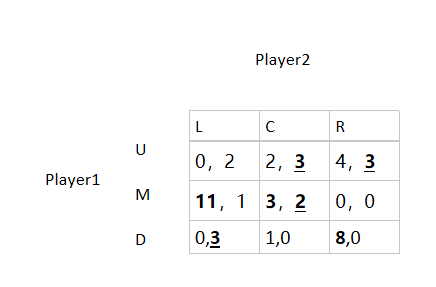
找出纳什均衡:
NE=(M,C)
因为相对于对方,每一名博弈者都做出了最佳对策。
注意:他们并没有选择最优策略,但是是无悔的。
Game Three--以囚徒困劲为例子理解:纳什均衡和严格占优的关联
之前讲过这个例子里面α相对于β是严格占优的(Player1 and player2)
BR1(α)=α
BR1(β)=α
BR2(α)=α
BR2(β)=α
则NE=(α,α)
结论:在纳什均衡点中不会有严格劣势策略
理由:严格劣势策略在任何时候都不会是最佳对应。
有一个问题:对于弱占优策略,这个结论并不成立
Game Four--弱占优策略
此时NE=(U,L) and (D,R)
如果2号博弈者选择R,1号博弈者的弱最佳对策是D
有时候NE会有很多,并不总是正确预测
Game Five--投资博弈:(协调博弈)
多方博弈,投资金额为$0或者$10,投资者不能互相交流(双向秘密)
有两个NE:都投资或者都不投资
如何找出NE? Guess and Check
Check is easy,只需要判断是否无悔
如果第一次博弈没有达到阈值(距离90%有一定距离),多次博弈之后,选择趋于消极结果。
反之,如果第一博弈达到了或者十分接近阈值(90)%,那么之后的博弈结果就可能趋向于积极结果。
这个消极结果不属于囚徒困境,理由是不存在严格劣势策略






