解决与腹地铁路网相连的码头间网络集装箱综合规划的禁忌搜索算法

A tabu search algorithm to solve the integrated planning of container on an inter-terminal network connected with a hinterland rail network

Qu Hu；Francesco Cormanb；Bart Wiegmansc；Gabriel Lodewijksd

摘要

几十年来，对集装箱的运输需求一直在增加，这给公路运输带来了压力。因此，刺激铁路运输提供更好的多式联运货运服务。本文研究了港区集装箱运输规划的数学模型，将集装箱的码头间运输（ITT，港区内）与铁路货运形成和运输过程（向腹地）相结合。整数线性规划模型用于制定跨集装箱码头运营的集装箱运输、连接它们的网络、铁路站场和通往腹地的铁路网络。提出了一种禁忌搜索算法来解决这个问题。在现实的基础设施案例和不同的需求场景中测试了算法的实际应用能力。我们的结果显示了内部 (ITT) 和外部（腹地）运输过程相互作用的程度，以及在使用建议的集成优化时改进整体运营的潜力。相反，如果将 ITT 系统中的集装箱规划作为一个独立的问题进行优化，铁路终点站可能会遭受更长的延误时间或额外的列车取消。在一天内规划 4060 TEU 集装箱的运输时，不考虑铁路运营的 ITT 规划的收益占 ITT 成本降低 17% 但铁路运营成本增长 93%，而 ITT 和铁路整合的收益占ITT 成本降低 20%，铁路运营成本降低 44%。

1 引言

集装箱运输在全球贸易中越来越重要。为满足日益增长的集装箱运输需求，主要集装箱港口均力图扩大规模。集装箱港口规模不断扩大，吞吐量更高；然而，这也导致了另一个问题：有效地将港口的集装箱码头连接到腹地运输服务网络。目前，公路运输占欧洲内陆货运的 75% 以上（欧盟统计局数据库，2014 年）。虽然公路运输提供更快、可靠和灵活的运输，但它有几个缺点，包括拥堵和负面环境影响，如排放和噪音滋扰。因此，有利于减少公路运输，促进铁路和内河航运的发展。为实现货车模式的转变，深海码头的集装箱应转移到铁路堆场或内河码头。这种移动可以通过终端间运输（ITT）进行。

这导致了以下两个操作问题：第一，使用可用的运输车辆在多个码头和铁路站场周围移动和重新安排集装箱流； 第二，安排装载集装箱列车并确定它们的出发时间。 前一期采用多码头间运输网络； 有效的运营对于减少网络外部（由进港船只）、码头运营以及运输部分产生的延误的影响至关重要。 目前，这是一个热门话题，也是一个明确的改进点，据鹿特丹港务局称，进出马斯平原二期的车辆中有超过 40% 经历了相当大的延误。 当 ITT 网络内发生延误时，下游操作（例如，在铁路站场装载列车）将受到影响，并可能导致额外成本：列车可能会延误甚至取消。

2 文献综述

2.1 车辆路径问题

本文中研究的 ITT 问题与车辆路径问题 (VRP) 非常相似，因为它们与给定网络上具有给定释放和交付时间的集装箱运输有关。 Dantzig 和 Ramser 于 1959 年首次制定了 VRP。VRP 从那时起演变为与寻找配送中心和多个客户之间的最佳交付路线相关的一系列问题。帕拉格等人 (2008a, 2008b) 对多个起点和目的地节点之间的传输问题进行了详细调查。根据帕拉格等人的说法。 (2008b)，我们研究中的 ITT 问题是带取货和送货的 VRP (VRPPD)。在我们的问题中，车辆访问取货点收集集装箱并将其运送到交货点。与典型的VRPPD相比，本文针对ITT网络在连通性、车辆密度、需求量和动态等方面的具体问题，不仅优化了港区内的配送路线，还考虑了相关铁路业务。根据VRPPD的结果制定列车装车和发车计划，减少延误和重新调度成本包含在VRPPD的目标中。我们简要回顾了与 ITT 网络和运营研究的特定方面相关的工作。

2.2 码头间运输

最近，ITT 受到越来越多的关注。 Heilig 和 Voβ (2017) 提供了有关 ITT 的文献概述，并指出需要协作规划来整合码头内和码头间的运营。由此，我们的研究研究了 ITT 和腹地铁路运输的整合，以降低这两个部分的成本。已经提出了几种优化模型来研究 ITT。 Tierney et al. (2014)了第一个使用时空网络图的 ITT 完全定义的数学模型。目标是尽量减少集装箱交货的延误。在时空网络图中，节点代表码头和交叉路口，加权弧代表道路。为了反映现实世界中的加载/卸载时间，引入了长期节点和长期弧。基于该图，作者提出了一个整数规划模型来解决 ITT 问题。在该模型中，考虑了 4 个码头和 2 个交叉路口，规划范围为 8 小时，时间步长为 5 分钟。 Nieuwkoop 等人(2014) 开发了时空模型，以找到具有最小延迟的最佳车辆配置。在这里，我们还使用了一个时空模型，它类似于 Tierney 等人提出的模型 (2014))，但我们扩展了模型以研究与腹地铁路运输作业相结合的更复杂的问题。我们使用 Nieuwkoop 等人提出的相同运输网络 (2014) 在案例研究中提出。我们不是在 ITT 中寻找最佳车辆配置，而是专注于研究最佳 ITT 交付和列车装载和发车计划，以降低总运营成本和延误成本。海利格等人(2017) 研究 ITT 卡车路线和减排​​。表明减少卡车的空载次数可以减少放。在我们的研究中，我们根据固定的车队规模优化了集装箱交付，这确保了空程的减少将提高我们的目标。

2.3 铁路运营

在铁路码头运营方面，Boysen 等人。 (2013) 对铁路码头运营问题和挑战进行了详尽的回顾。许多研究集中在火车装卸问题上。大多数研究人员使用混合整数规划 (MIP) 模型来描述加载和卸载过程。 Corry 和 Kozan (2007) 提出了一种分配模型，用于将集装箱动态分配到多式联运终端的火车槽位。 Li 和 Wang (2008) 使用基于模拟的算法来寻找（卸载）集装箱列车时叉车和集装箱卡车的最佳部署。安吉诺菲等人(2011) 提出了一种规划程序，用于在具有水平装卸设备的铁路网络中满足货物运输要求。尽管对铁路终点站的运营进行了深入研究，但很少有研究以综合方式调查铁路终点站与 ITT 之间的协调。卡巴利尼等人 (2014) 提出了一种通过采用所考虑系统的基于队列的离散时间模型来优化海港码头铁路运营的规划方法。

整合铁路运输的优化很有趣，例如，参见 Corman 等人讨论的论文 (2016)。 我们方法的一个关键点是与铁路运营的整合。 事实上，为了确保将集装箱及时运送到最终目的地，我们认为铁路运输过程的整合是必要的和相关的扩展。

3 有铁路连接和运输业务的 ITT 网络

在我们的研究中，我们研究了从集装箱在码头放行的那一刻起，直到它们在港区内的另一个码头或腹地运送到目的地为止的集装箱运输过程。我们的目标是降低总体成本，这由多项贡献组成。在ITT部分，我们通过安排车辆的路线和集装箱的交货顺序以及集装箱何时何地放行和应交付的信息来降低车辆的行驶成本和集装箱延误成本。在铁路运营环节，任何延误的集装箱都无法按时装车，可能会影响列车的发车计划。成本与延误罚款以及火车装载率低时增加的成本有关。如果火车晚点太多集装箱，火车将被取消。我们的研究整合了所有这些流程，以降低总运营成本和延迟成本。这对于优化利用 ITT 网络中的可用容量以及允许货运列车及时、经济高效地发车非常重要。

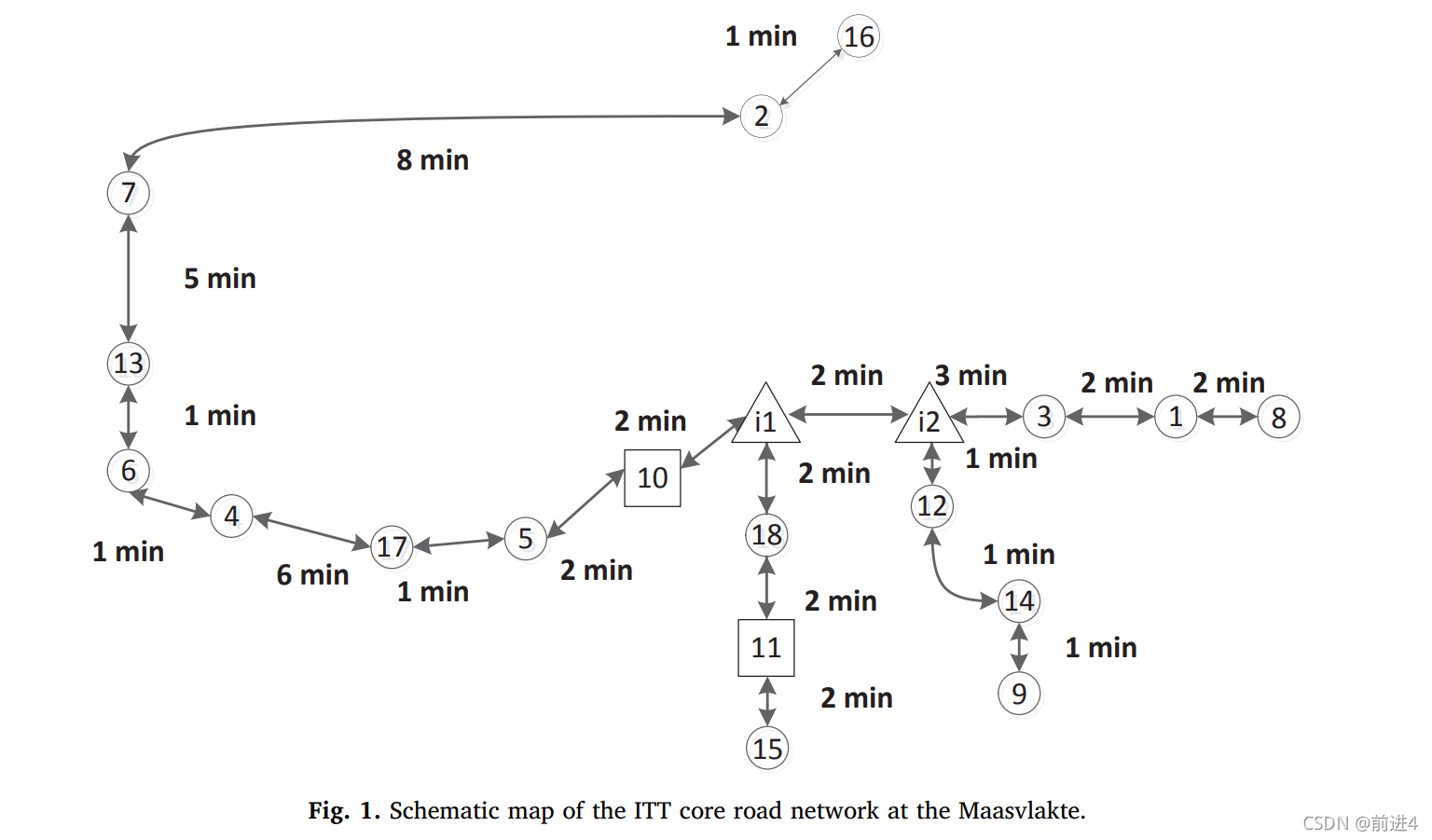
在本文中，数学模型是通用的，能够表示由码头、道路连接和交叉口组成的 ITT 网络的不同布局。 为了更清楚地解决所研究的问题，我们以 Maasvlakte1&2 的运输网络为例，分析 ITT 的优化组织和运营。 Nieuwkoop 等人 (2014) 研究了 Maasvlakte1 和 2 码头之间的道路连接和运输需求。 为了降低复杂性并加强 ITT 与铁路运输之间的关系，我们考虑了 ITT 网络的示意图（见图 1）。 我们在一天内研究了该网络中的 ITT 和铁路运营，时间分辨率为一分钟。

ITT网络由20个节点和19条链路组成。 在20个节点中，18个节点代表码头，2个节点代表交叉点（i1和i2）。 我们假设 18 个码头通过公路运输网络连接。 10 号和 11 号码头是连接腹地铁路网的专用铁路终点站。 节点 i1 和 i2 代表两个三向路口。 在本节的其余部分，我们将描述该系统中的节点、链接和相关操作。

3.1 系统中的节点和链接：码头、交叉路口和道路链接

3.1.1 码头节点

在 ITT 网络中，假设有两种类型的码头，即海运码头和铁路码头。 在本研究中，我们假设除 10 和 11 之外的所有码头都是海运码头。 在海运码头，使用码头起重机从船上卸下集装箱。 然后将集装箱移动到存储区域。 将集装箱从海运码头运输到目的地的车辆必须进入堆垛块的末端。

除了海运码头，我们还考虑了铁路码头，即 10 和 11。在典型的铁路码头中，车辆可以使用铁路轨道旁边的车道，起重机用于在列车、堆场和堆场之间搬运集装箱。

3.1.2 交叉路口

交叉路口可能会增加车辆在网络中的行驶时间。 在本文中，网络中仅使用了三向交叉路口。 为了识别交叉点中的潜在冲突，我们添加了一个虚拟节点“O”来反映交叉点的中心（见图 2）。 那么，在该交叉点可以找到六个方向，其中三个方向发生冲突，即 A-O-B、C-O-A 和 B-O-C。 虽然一些车辆可以在不阻塞其他车辆路线的情况下穿过交叉路口，但只有有限数量的车辆可以在一个时间步长内穿过虚拟节点 O 而不降低它们的速度。

3.1.3 系统链接：公路运输网络

上述18个码头通过道路网络连接，如图1所示。如果集装箱需要从一个码头移动到另一个码头，集装箱将进入ITT网络。 我们将运输需求定义为任务。 每个任务由 1 或 2 个 TEU 集装箱组成，具有给定的始发站、目标站和交货时间窗口。 具体来说，任何运输任务只能在发布时间后从其始发地取货，并应在到期时间之前交付到目的地。

3.2 节点、交叉路口和链接的相关假设

3.2.1 海运、铁路码头装卸作业

在海运和铁路码头，我们假设集装箱可以在其释放时间后立即装载到车辆上。 我们还假设，如果码头中有多个可执行任务，则将首先运输到期时间最早的任务。

3.2.2 铁路码头列车编队

在一个铁路码头，每天计划有一定数量的列车，不同的发车时间和装载集装箱的容量。 我们根据以下标准确定列车的实际发车时间：如果列车在计划发车时间未满载，则该列车将延误。 在本文中，我们为每列火车设置了固定的缓冲时间，因此只允许在缓冲时间内出现延迟。 博伊森等人 (2010) 还指出，只有在列车满载的情况下，列车才能盈利。 在缓冲时间结束时列车未满载的情况下，装载超过η（例如容量的75%或80%）的列车将出发； 否则，火车将被取消。

在这项研究中，我们使用了一个中等时间范围（一天），因此我们无法估计第二天集装箱的实际运输时间。 此外，留在码头的集装箱会影响第二天的集装箱运输，这可能会导致额外的成本。 因此，为了计算延误成本，我们假设错过接驳列车的集装箱将由卡车运输到腹地。 在 Behdani 等人 (2014) 中可以找到类似的假设。 未来的研究可以集中在更长的时间范围和确定单元列车频率的可能性。

3.2.3 交叉口运输操作：拥堵

考虑到 ITT 网络的短行程时间，例如，图 1 中链接的平均行驶时间为 2.4 分钟，交叉口造成的延迟时间比在更大的交通网络中更显着。 我们的研究还表明，如果使用更多的 ITT 车辆或移动更多的集装箱，交叉路口的等待时间会增加。 为了管理交叉口内的拥堵，我们设置 S 来限制进入交叉口的车辆数量。 我们假设交叉路口的容量等于每时间步长（1 分钟）2 辆车。

3.2.4 链路上的运输

一般来说，有几种车辆经常用于码头之间的集装箱运输：载人卡车，通常容量为 2 TEU； 多拖车系统 (MTS)，最多可拉动五个底盘； 自动导引车 (AGV)，可在现有海运码头以高达 20 公里/小时的速度运输一个 40 英尺集装箱或两个 20 英尺集装箱； 自动起重车 (ALV)，能够在平台上提升集装箱，将起重机和车辆之间的装卸操作分离。

在 Duinkerken 等人中 (2006) 将 ITT 系统与 AGV、ALV 和 MTS 进行比较，计算车辆的行驶时间时不考虑拥堵。 在我们的论文中，容量为 2 TEU 的载人卡车用作 ITT 网络中的车辆。 卡车的平均速度设置为 30 公里/小时，每个链接的行驶时间如图 1 所示。我们还假设链接上没有发生拥堵。

鉴于 ITT 网络的规模，卡车的起始位置和车辆的第一个任务之间的距离可能非常短； 我们做了另一个假设，卡车的路线总是从第一个任务开始，到最后一个任务结束，因此，在规划范围的开始或结束时没有车辆移动。 Heilig 等人也做出了类似的假设 (2017)：到达第一个位置的行程不计为空行程，目标函数中不考虑返回初始位置的行程。 根据经验，这不会导致目标函数发生显着变化。

4 数学模型

5 禁忌搜索

6 数值实验

7 结论