校外实训、程序实践--深搜、递归算法

本文主要是介绍校外实训、程序实践--深搜、递归算法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

·DFS（深度优先搜索）讲解

·讲解

第三章搜索与图论（一） - AcWing

·简介

dfs和递归其实差不多就是一个道理

看成一个执着的人

尽可能往深里搜，搜到头了才回溯

且不是回溯到最先，而只返回一次（一个结点），然后看是否可以继续往内

“回溯”与“剪枝”：

1、回溯是由系统自己来实现的

！！！回溯回来的时候（递归函数结束的时候）紧接着要恢复现场！！

//每一题的恢复现场的意思各有不同，自己理解

【在进入到下一层之前我们修改了状态，下一层执行完之后，记得马上恢复原来的状态（变之前的状态）】

2、剪枝的意思就是判断当前所填是否合法，合法再填，不合法就不填

每一个dfs都对应一个搜索树

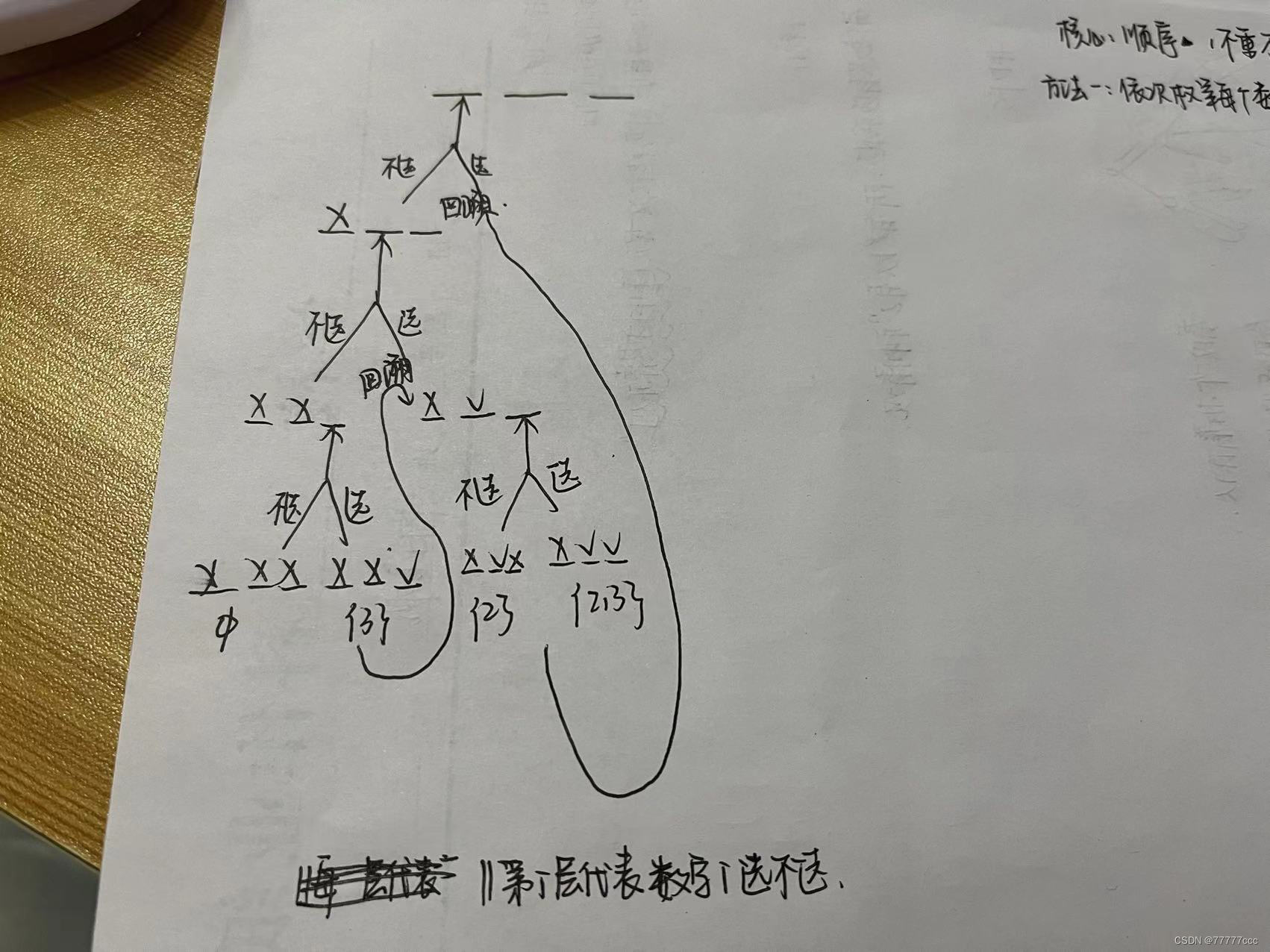
·思考顺序：

先画递归树，用递归树理清楚我们如何不重不漏地暴力搜索出所有情况

然后再回到代码，考虑如何用代码实现我们的思路

·重点

dfs其实就是暴搜（用递归把每一种情况遍历一遍）

一定要考虑清楚要用什么样的顺序遍历我们所有的方案

·例题讲解

·递归实现排列型枚举

讲解：

AcWing 842. 排列数字 - AcWing

蓝桥杯C++ AB组辅导课（试听课）_哔哩哔哩_bilibili

分析：

一位一位往后填，然后每次填的和前面的不能一样

注意注意注意：回溯的时候一定要注意恢复现场----用完的东西都要还回去

比如说图中的回溯，记得恢复成1_ _ 的状态

！！！回溯回来的时候（递归函数结束的时候）紧接着要恢复现场！！

【在进入到下一层之前我们修改了状态，下一层执行完之后，记得马上恢复原来的状态】
#include <iostream>
using namespace std;const int N=10;
int n;
int path[N];
//存下来每次分支的状态
bool used[N]; 
//默认初始化为0 也就是false
//用来记录每个分支的时候，哪些已经被用过了，也就是可以知道那些数字可以用
//因为本题说数字不能重复void dfs(int u)
{if(u==n)//意味着每一个下标都已经填过了{//便可以输出出来这个路径for(int i=0;i<n;i++)cout<<path[i]<<" ";cout<<endl;}else{for(int i=1;i<=n;i++)//i枚举一下当前的位置可以填哪些数{if(!used[i])//这个数字没有被用过{path[u]=i;//填入当前的位置used[i]=true;//把这个位置处理完了，那就处理下一层（下一个位置）dfs(u+1);//当上面这个代码执行完，相当于在回溯的时候了，那就要恢复成原来的样子//path[u]=0;  //但是这个没必要写，因为每次填数的时候会覆盖过去used[i]=false;}}	}
}int main()
{cin>>n;dfs(0);//从0下标开始填数return 0;
}

·递归实现指数型枚举

·自己的思考：

此题和上面那题看似一样

但是首先两者的要求不一样，本题要求位数是从1到n都要考虑

本题在考虑有顺序地把每一种情况不重不漏都考虑出来时，用了下述视频里面的方法，和上面那一题的方法还是不大一样的

本题每一个树层u，考虑的是数字u填或者不填，而上面那一题是每一层都枚举1到n，看看哪些数字是可以填的（也就是之前没有填过，因为题目要求不重复数字）

·讲解：

蓝桥杯C++ AB组辅导课（试听课）_哔哩哔哩_bilibili

//1:14:13开始

·题目：

·分析：

递归最重要的就是考虑顺序，就是用什么样的方式把每一种情况不重不漏都考虑出来

我们本题方式就是：依次考虑1到n每一个数，然后选或者不选

·代码：

--我的代码
#include <iostream>
using namespace std;const int N=15;int path[N];
int n;void dfs(int u)
{if(u==n){for(int i=0;i<n;i++){if(path[i]!=0)cout<<path[i]<<" ";}	cout<<endl;}else{	path[u]=0;dfs(u+1);path[u]=u+1;dfs(u+1);}
}int main()
{cin>>n;dfs(0);return 0;
}
--yxc代码
#include <iostream>
using namespace std;const int N=15;int stu[N];//用来记录每个位置的状态，0表示还没考虑，1表示选它，2表示不选它
int n;void dfs(int u)
{if(u>n){for(int i=1;i<=n;i++){if(stu[i]==1)printf("%d ",i);}	cout<<endl;}else{	stu[u]=2;//第一个分支：不选dfs(u+1);    //考虑后面的位stu[u]=0;//恢复状态：这一位还没有考虑stu[u]=1;//第二个分支：选它dfs(u+1);   //考虑后面的位stu[u]=0;//恢复状态：这一位还没有考虑}
}int main()
{cin>>n;dfs(1);return 0;
}

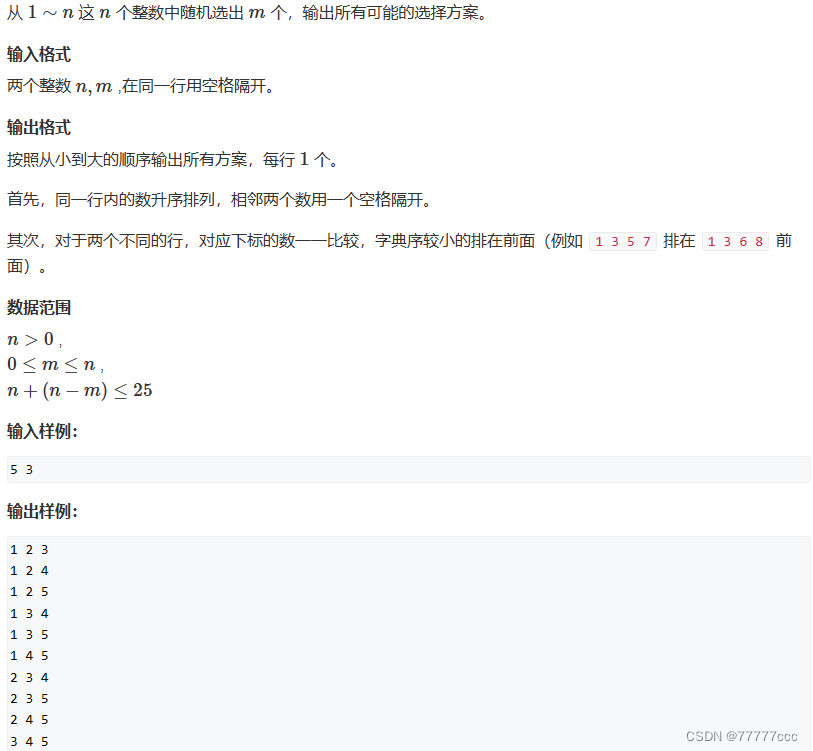
·递归实现排列型枚举

·讲解：

AcWing 93. 递归实现组合型枚举 - AcWing

AcWing 93. 递归实现组合型枚举（每日一题·春季） - AcWing

#include <iostream>
using namespace std;const int N = 30;int n,m;
int path[N];void dfs(int u,int start)
{if(u>m){for(int i=1;i<=m;i++)printf("%d ",path[i]);}else{for(int i=start;i<=n;i++)//从start开始搜（枚举），保证是递增的{path[u]=i;dfs(u+1,i+1);path[u]=0;//恢复现场}}
}int main()
{scanf("%d%d",&n,&m);dfs(1,1);return 0;
}
说明：由于我们用的是数组，每次填数的时候都会覆盖掉，所以恢复现场在此看来可有可无，但如果用的是vector的话，恢复现场就很重要了-----pock_back() 掉

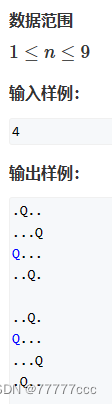
·n皇后问题

·讲解：

第三章搜索与图论（一） - AcWing

#include <iostream>
using namespace std;const int N = 20;  //对角线个数是2N-1int n;
char g[N][N];
bool col[N],dg[N],udg[N];
//col表示列是否填过
//dg表示递减的对角线是否填过
//udg表示递增的对角线是否填过void dfs(int u)
{if(u==n){for(int i=0;i<n;i++)puts(g[i]);puts("");return ;}for(int i=0;i<n;i++)//当前这一行的皇后，应该放在哪一列if(!col[i]&&!dg[u+i]&&!udg[i-u+n]){g[u][i]='Q';col[i]=dg[u+i]=udg[i-u+n]=true;dfs(u+1);col[i]=dg[u+i]=udg[i-u+n]=false;g[u][i]='.';}
}
int main()
{cin>>n;for(int i=0;i<n;i++){for(int j=0;j<n;j++)g[i][j]='.';}dfs(0);//最初的表格都是. return 0;
}

·2的幂次方表示

·讲解：

AcWing 3483. 2的幂次方（每日一题·夏季） - AcWing

·题目
#include <iostream>
#include <bitset>
#include <string>
#include <vector>
using namespace std;string dfs(int n)
{string res;for(int i=14;i>=0;i--){if(n>>i&1)//这个二进制位上的数如果是0，那就不用管//这个二进制位上的数如果是1，那就进入大括号内//然后就相当于是写成2^i //判断i是0,1，>=2{if(res.size())res+='+';if(!i)res+="2(0)";else if(i==1)res+="2";elseres+="2("+dfs(i)+")";}}return res;
}
int main()
{int n;cin>>n;cout<<dfs(n)<<endl;return 0;
}
易错点：每一次传入i（或者说每一次进入新的递归的时候），都会有“自己的res”，每次的res存的就是当前的这个数的拆分结果，不要误认为是只有一个res了

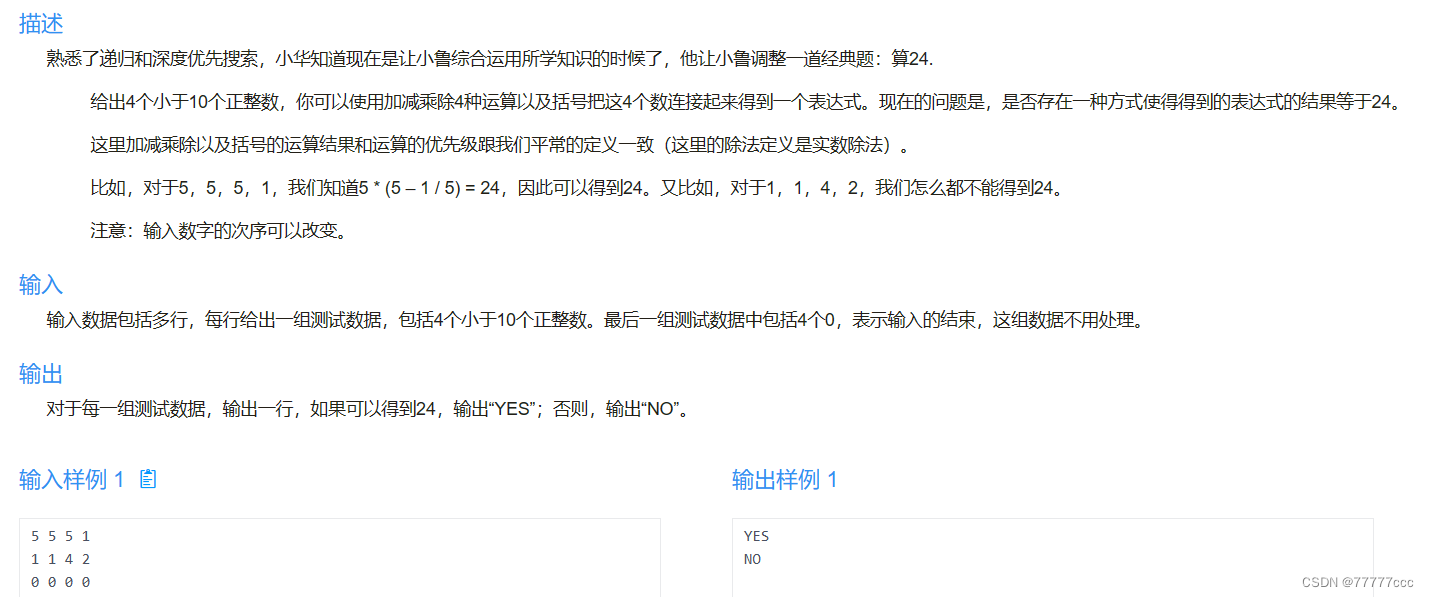
·算24

·难点：找到递归的点！！！明白怎么个递归法，就是找到一个顺序，能够枚举出所有的可能情况

再用递归实现这个枚举

·思路：

n个数算24，必有两个数要先算。

这两个数算的结果，和剩余n-2个数，就构成了n-1个数求24的问题

因此，将“4个数算24点”转换为规模较小的“3个数算24点”，再转换为规模较小的“2个数算24点”，最后转换为“1个数算24点”。

解法：把原问题n个数中的任意两个数通过4种运算符得到一个新数，再把其并入剩下的n-2个数。问题变成求解n-1个数的算24点问题。

边界：当只剩一个数的时候，看它是否为24（浮点数判断相等与否注意）
#include <iostream>
using namespace std;#include <iostream>
#include <cmath>
using namespace std;const int EPS = 1e-6;
double inputnumber[4];bool iszero(double x)
{return fabs(x)<=EPS;
}bool count24(double a[],int n)
{if(n==1){if(iszero(a[0]-24))return true;elsereturn false;}else{for(int i=0;i<n-1;i++)for(int j=i+1;j<n;j++){double temp[n-1]={0};int itemp=0;for(int k=0;k<n;k++){if((k!=i)&&(k!=j))temp[itemp++]=a[k];}temp[itemp]=a[i]+a[j];if(count24(temp,n-1))return true;temp[itemp]=a[i]*a[j];if(count24(temp,n-1))return true;temp[itemp]=a[i]-a[j];if(count24(temp,n-1))return true;temp[itemp]=a[j]-a[i];if(count24(temp,n-1))return true;if(!iszero(a[i])){temp[itemp]=a[j]/a[i];if(count24(temp,n-1))return true;}if(!iszero(a[j])){temp[itemp]=a[i]/a[j];if(count24(temp,n-1))return true;}}return false;}
}
int main()
{while(true){bool isendinput=true;for(int i=0;i<4;i++){cin>>inputnumber[i];if(!iszero(inputnumber[i]))isendinput=false;}if(isendinput)break;if(count24(inputnumber,4))cout<<"YES"<<endl;elsecout<<"NO"<<endl;}return 0;
}

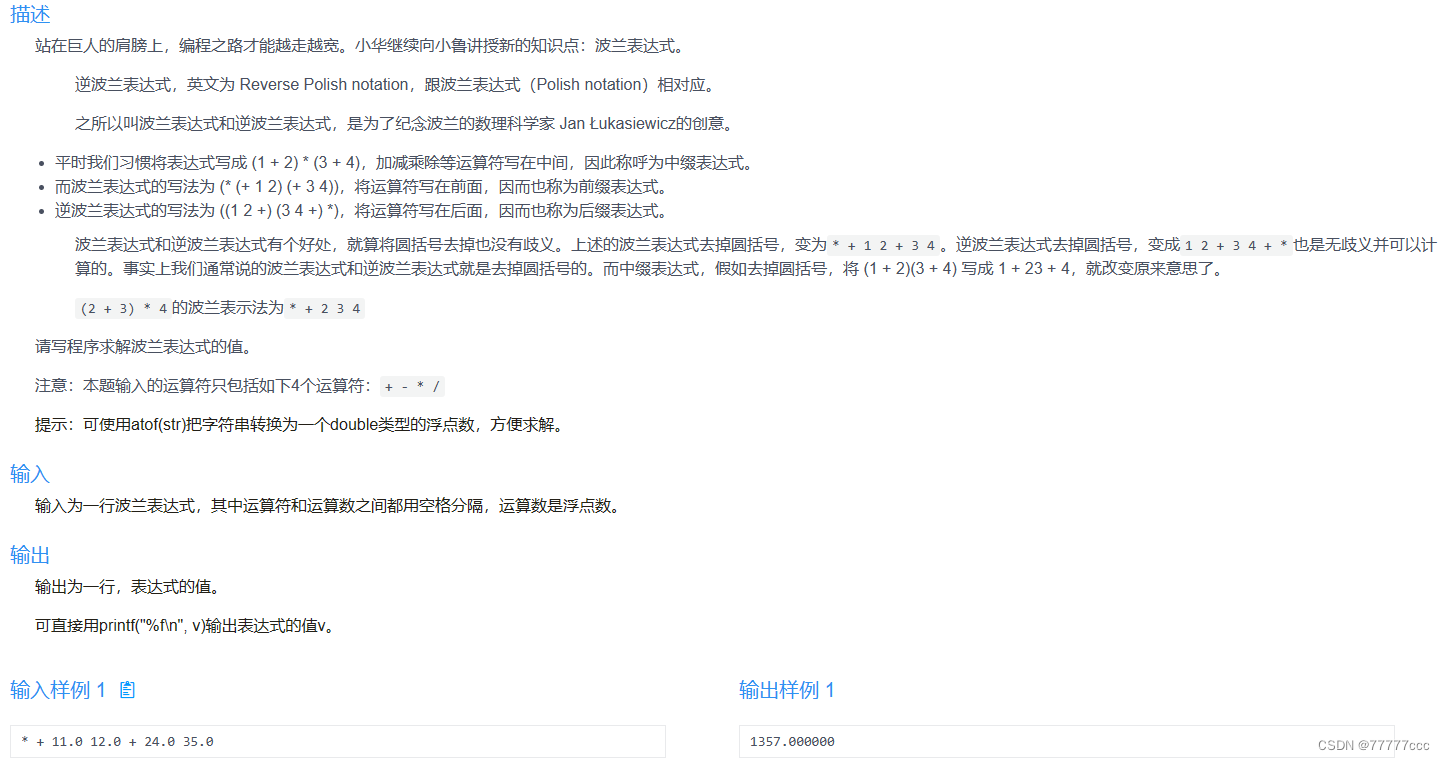
·波兰表达式

#include <iostream>
using namespace std;//有空格 所以一次读入的就是一个小部分，不会把整个str都读完了
//cin>>str 不会读入空格
double p()
{string str;cin>>str;//每一次进入递归都读入 因为题目所给的字符串是有空格的！！switch(str[0]){case '+':return p()+p();case '-':return p()-p();case '*':return p()*p();case '/':return p()/p();default:return stof(str);break;}
}
int main()
{printf("%f\n",p());return 0;
}

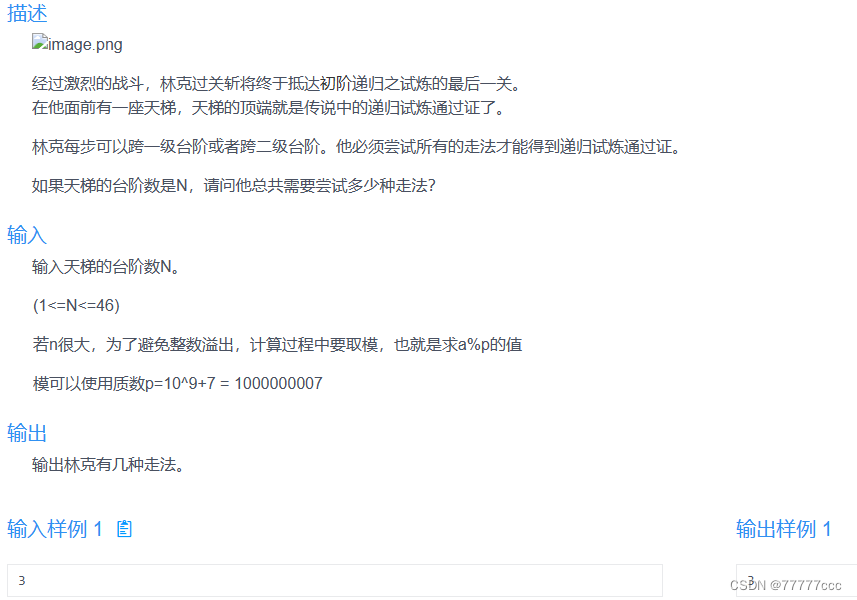
·爬天梯

#include <iostream>
using namespace std;int n;
const int N = 1000000;
const int MOD=1000000007;int a[N];int dfs(int n)
{if(n<=1)return 1;if(a[n]!=0)return a[n];else{a[n]=dfs(n-1)+dfs(n-2);a[n]%=MOD;}return a[n];
}
int main()
{scanf("%d",&n);printf("%d\n",dfs(n));return 0;
}

注意：排列的那种思想，在递归里大部分确实适用。

但是并不是说所有递归题目都一定是那种思想，当觉得不适用时，可以换个思路角度！

·深搜的例题

·命运之城

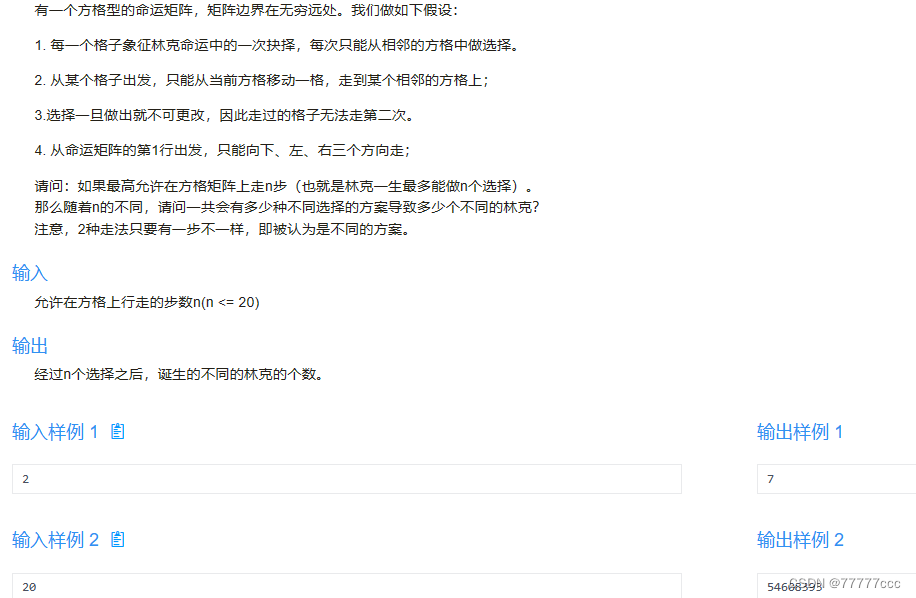
从 (i,j) 出发，走n步的方案数，等于以下三项之和：

从(i+1,j)出发，走n-1步的方案数。

从(i,j+1)出发，走n-1步的方案数。

从(i,j-1)出发，走n-1步的方案数。

分析见下图代码注释

#include <iostream>
using namespace std;typedef long long LL;
const int N=70;
int n;int used[N][N];
//标记那一个位置有没有走过
//因为题目要求只能走没有走过的
//0没走过，1走过
int dx[3]={1,-1,0};
int dy[3]={0,0,-1};
//答案有几步就是函数dfs的返回值LL dfs(int i,int j,int u)
{if(u==n+1)return 1;//i,j表示当前位置的坐标//n表示当前走第几步used[i][j]=1;LL res=0;for(int k=0;k<3;k++){int x=i+dx[k];int y=j+dy[k];if(used[x][y]==0){res+=dfs(x,y,u+1);}}used[i][j]=0;return res;
}
int main()
{cin>>n;printf("%ld\n",dfs(N/2,0,1));return 0;
}

·红与黑

讲解：AcWing 1113. 红与黑（寒假每日一题） - AcWing

#include <iostream>
using namespace std;typedef long long LL;
const int N=27;
char state[N][N];
int maxx;
int maxy;
int fx;
int fy;
int res=0;int dx[4]={-1,0,1,0};
int dy[4]={0,1,0,-1};int dfs(int i,int j)
{int res=1;  //这里记得！！！state[i][j]='#';for(int k=0;k<4;k++){int x=i+dx[k];int y=j+dy[k];if(x>=0&&y>=0&&x<maxy&&y<maxx&&state[x][y]=='.'){res+=dfs(x,y);}}return res;
}
int main()
{while(cin>>maxx>>maxy,maxx!=0){for(int i=0;i<maxy;i++)for(int j=0;j<maxx;j++){cin>>state[i][j];if(state[i][j]=='@'){fx=i;fy=j;}}printf("%d\n",dfs(fx,fy));}return 0;
}

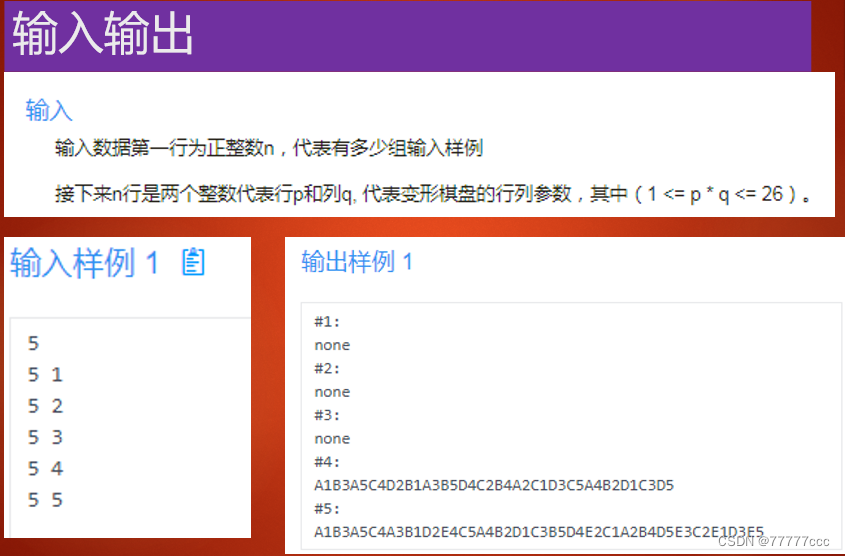
·骑士的怜悯1

思路：
1、八个跳跃的方向，用dx[]和dy[]列出来（按照字典序列），要一一枚举

2、在主函数里面依次枚举每一个格子作为起点，分别调用dfs进行深搜，一旦有一个可以了就break，此时这个情况便就是字典序最小的那一种情况。如果枚举了所有的点都找不到情况

那便是输出none了

3、坐标用pair<char,int>存储本题第一维坐标是字符第二维坐标是数字

4、dfs函数的返回值不是数字，而是bool类型

#include <cstring>
#include <iostream>
#include <utility>
#include <vector>using namespace std;const int N=27;
int p,q;
bool st[N][N];
vector<pair<char,int>> path;
//用这个来存储马的跳跃路径int dx[8]={-2,-2,-1,-1,1,1,2,2};
int dy[8]={-1,1,-2,2,-2,2,-1,1};
//按照字典序存储8个方向
//因为我们要求输出字典序最小的一种
//所以首先枚举的就要是字典序最小的路径//dfs的返回值有的是bool 有的是值int或者ll
//根据情概况判断用哪一种//当前的坐标 和 跳了多少步
bool dfs(int x,int y,int cnt)
{//x,y 这一步跳path.push_back({char(x+'A'),y+1});st[x][y]=true;//出口：跳了p*q步if(cnt==p*q){for(auto a:path)cout<<a.first<<a.second;return true;}for(int i=0;i<8;i++){int a=x+dx[i];int b=y+dy[i];if(a<0||a>=q||b<0||b>=p)continue;if(st[a][b])continue;if(dfs(a,b,cnt+1))return true;}//恢复现场st[x][y]=false;path.pop_back(); //删除刚刚填入的那一步路径return false;//这一步不要忘！！！//比较特殊的一步//因为如果上面的true出口没有//说明没有走法，记得返回fasle
}
int main()
{int t;cin>>t;for(int i=1;i<=t;i++){cout<<"#"<<i<<":"<<endl;cin>>p>>q;//初始化path.clear();memset(st,0,sizeof(st));bool flag=false;//因为有多个位置作为起点//只要有一种起点可以//那么就有答案//棋盘的每个位置都作为深搜的起点for(int i=0;i<q;i++)for(int j=0;j<p;j++){if(dfs(i,j,1)){flag=true;break;//只要字典序最小的那种//也就是我们枚举到的第一种}}if(!flag)cout<<"none";cout<<endl;}
}

·数独检查

讲解：AcWing 703. 数独检查（寒假每日一题） - AcWing

五个判定条件：

记忆碎片的行列都是9×9，并且里面没有非法字符(1-9)

记忆碎片A与原始矩阵A，非空位置的数字要完全相同

记忆碎片A的每一行1-9都无重复

记忆碎片A的每一列1-9都无重复

记忆碎片的每一个3*3的格子内，数字1-9无重复

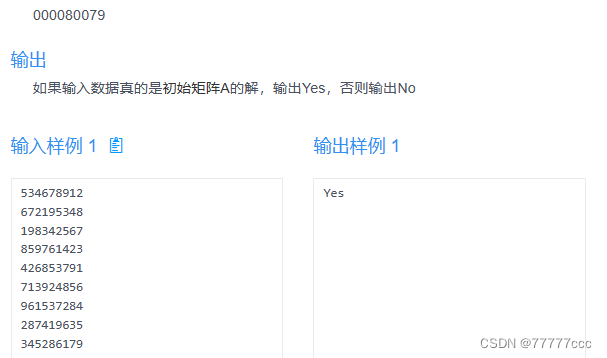
#include <cstring>
#include <iostream>
using namespace std;const int N=9;
const int M=3;string memory[N]={{"530070000"},{"600195000"},{"098000060"},{"800060003"},{"400803001"},{"700020006"},{"060000280"},{"000419005"},{"000080079"}};int a[N][N],b[N][N]; //两个要比较的矩阵
bool st[N+1]; //判断1到9这八个字符是否被使用过bool check_input()//在这个函数里面，判断输入的是否合法
{               //如果合法，存到矩阵b中string line;for(int i=0;i<N;i++){cin>>line;if(line.size()!=N) return false;for(int j=0;j<N;j++){int t=line[j]-'0';if(t<0||t>N)return false;if(a[i][j]!=0&&a[i][j]!=t)return false;b[i][j]=t;}}return true;//要会利用函数return的特点//对于这种多判断条件的//最后来一个return 就是上面那些情况都不是时，就走这一条路！！
}bool check_row()
{for(int i=0;i<N;i++){memset(st,false,sizeof(st));for(int j=0;j<N;j++){int t=b[i][j];if(st[t]) return false; //一旦有，就return false出函数了st[t]=true;}}
}bool check_col()
{for(int i=0;i<N;i++){memset(st,false,sizeof(st));for(int j=0;j<N;j++){int t=b[i][j];if(st[t]) return false;st[t]=true;}}return true;
}bool check_block()
{for(int x=0;x<N;x+=M){for(int y=0;y<N;y+=M){memset(st,false,sizeof(st));for(int dx=0;dx<M;dx++){for(int dy=0;dy<M;dy++){int t=b[x+dx][y+dy];if(st[t]) return false;st[t]=true;}}}}return true;
}
int main()
{for(int i=0;i<N;i++)for(int j=0;j<N;j++)a[i][j]=memory[i][j]-'0';if(check_input()&&check_row()&&check_col()&&check_block())cout<<"Yes"<<endl;elsecout<<"No"<<endl;return 0;
}

·填数独1

讲解：AcWing 1613. 数独简单版（寒假每日一题） - AcWing

如何判断当前填法是否合法：

开三个bool数组----

存每一行某个数是否填过

存每一列某个数是否填过

存每个小方块某个数是否填过

每次填完之后，回溯的时候，三个数组的状态记得更新一下！！！

我的思路太慢，而且写起代码来要很长：我想的是填入这个数，然后搜索看同一行有没有重复等，这样子代码太慢，太长

数组标记法要会用！！！！！！
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;const int N =10;
int g[N][N];
bool row[N][N],col[N][N],cell[3][3][N];bool dfs(int x,int y)
{//这个坐标变换方法学起来if(y==9){x++;y=0;}if(x==9) //表示填完了{for(int i=0;i<9;i++){for(int j=0;j<9;j++){cout<<g[i][j];}cout<<endl;}return true;}if(g[x][y]!=0)return dfs(x,y+1);else{for(int i=0;i<9;i++){if(!row[x][i]&&!col[y][i]&&!cell[x/3][y/3][i]){g[x][y]=i+1;row[x][i]=col[y][i]=cell[x/3][y/3][i]=true;if(dfs(x,y+1))return true;row[x][i]=col[y][i]=cell[x/3][y/3][i]=false;g[x][y]=0;}}}return false;
}
int main()
{std::ios::sync_with_stdio(false);std::cin.tie(NULL),std::cout.tie(NULL);for(int i=0;i<9;i++)for(int j=0;j<9;j++){char ch;cin>>ch;int t=ch-'0';g[i][j]=t;if(t!=0)row[i][t-1]=col[j][t-1]=cell[i/3][j/3][t-1]=true;}dfs(0,0);return 0;
}
dfs返回值类型为bool 理解一下其中代码的返回值方面的处理！！

·填数独2----可行性剪枝（优化搜索顺序）

讲解：AcWing 166. 数独 - AcWing

基本顺序思路：

每一次随意挑选一个空白格子

枚举该格子选哪个放

dfs

但是因为数据比较强，如果这样优化的话，会发现超时了

所以对基本顺序思路的前两部做优化

【插入】搜索里面常用的剪枝方法有哪些

1、优化搜索顺序，优先搜索决策数少的开始搜

2、排除冗余信息

3、可行性剪枝：如果已经知道当前分枝往下走的话已经没有答案了，那就不再往下走了

4、最优性剪枝：如果往下搜发现最优解都比当前答案大，那就不往下走了

本题优化：

1、优化搜索顺序 --------优先选择能填数字最少的位置（优化深搜的起点，减少搜索树的宽度）

2、可行性剪枝 --------某个位置无数可填就回溯

3、对每棵树采用位运算进行“常数优化”

老师ppt笔记：

对于每行、每列、每宫，分别用一个9位的二进制(全局整数变量)，保存哪些数字还可以填。

对于每个位置，使用二进制的&运算求交集，并且使用lowbit运算取出每个可填的位置更新状态：采用二进制运算迅速更新行、列、宫的状态值

#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 9, M = 1 << N;int map[M], ones[M];
int row[N], col[N], cell[3][3];
char g[100];/*二进制优化：1：表示待填0：表示已填搜索+剪枝优化搜索顺序：从分支少的点开始搜，即可选填法最少的开始搜索可行性剪枝：自然行列和九宫格不能重复位运算优化：使用位运算（九个二进制位）表示行列九宫格已填数字对于当前位置可选方案的判断：row[x] & col[y] & cell[x / 3][y / 3] ---> 即可得到该位置在三个方向共同可以填的数的方案！为了方便获得对应二进制位1的个数用于统计是否是分支最少的点的时候，可以使用数组预处理0-2^9的数中的1的个数为了方便获得对应二进制位1对应的0-9可以预处理map得到2^i与i的映射关系！--> 对应数组 t = map[lowbit(x)]*/// 初始化操作：全部设置为9个1
void init(){// 行列for(int i = 0; i < N; i ++) row[i] = col[i] = (1 << N) - 1;// 九宫格for(int i = 0; i < 3; i ++)for(int j = 0; j < 3; j ++) cell[i][j] = (1 << N) - 1;
}// 填充和恢复操作
// x,y点处填入数字t，is_set：表示是填充还是恢复
void draw(int x, int y, int t, bool is_set){// 1. 处理字符串填充和恢复if(is_set) g[x * N + y] = '1' + t;else g[x * N + y] = '.';// 2. 处理二进制标记数组填充和恢复// 使用二进制表示哪个位置填了或未填！int v = 1 << t;// 若为恢复则取相反数，即原来-v，恢复则为-(-v)即为+v，即可恢复回去！if(!is_set) v = -v;row[x] -= v, col[y] -= v, cell[x / 3][y / 3] -= v;
}// 返回最后一个1
int lowbit(int x){return x & -x;
}// 返回x行j列该位置的可填数字情况
int get(int x, int y){return row[x] & col[y] & cell[x / 3][y / 3];
}bool dfs(int cnt){// 没有需要填的位置，直接返回if(!cnt) return true;// 选择可选分支最少的，属于剪枝优化之优化搜索顺序！int minv = 10, x, y;for(int i = 0; i < N; i ++)for(int j = 0; j < N; j ++)if(g[i * N + j] == '.'){int status = get(i, j);// ones：表示当前状态的1的个数，即可填方案数if(ones[status] < minv){minv = ones[status];x = i, y = j;}}int status = get(x, y);// 枚举每一种填法for(int i = status; i; i -= lowbit(i)){// 获取最后一位1对应的2的指数幂对应的幂，即获取该位置应该填 1-9的谁int t = map[lowbit(i)];// 填写数字draw(x, y, t, true);// 处理下一个填写位置if(dfs(cnt - 1)) return true; // 恢复现场draw(x, y, t, false);}return false;
}int main(){// 预处理 2^i 与 i 的映射for(int i = 0; i < N; i ++) map[1 << i] = i;// 预处理0-2^9的数中每个数中1的个数for(int i = 0; i < 1 << N; i ++)for(int j = 0; j < N; j ++)ones[i] += i >> j & 1;while(cin >> g, g[0] != 'e'){// 初始化行列和九宫格二进制位都为1init();// 统计需要填充位置int cnt = 0;for(int i = 0, k = 0; i < N; i ++)for(int j = 0; j < N; j ++, k ++)if(g[k] != '.'){// 将一长串字符串转化到 行列九宫格 的二进制为用0表示int t = g[k] - '1';draw(i, j, t, true);}else cnt ++;dfs(cnt);cout << g << endl;}return 0;
}

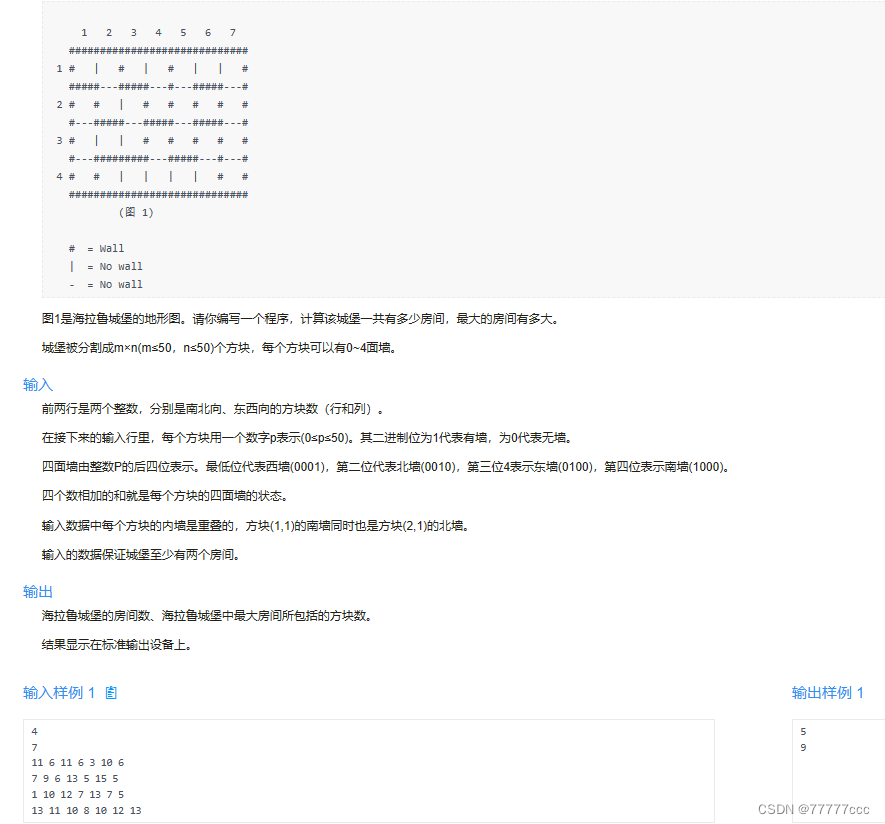
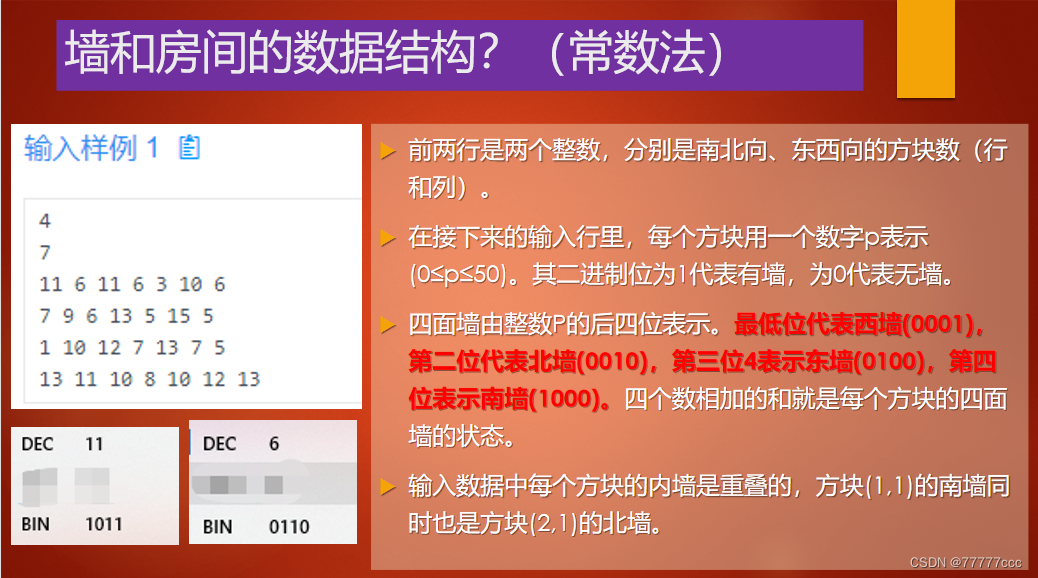
·城堡问题

解题思路：

使用深度优先搜索得到从某个顶点开始的最大连通子图

对每个连通子图做同一种颜色标记(flood Fill算法)

用全局二维数组Color[Row][Column]存储相应方块的颜色

注意：Color[i][j]初始值为0，表示方块[i][j]还没有访问

#include <algorithm>
#include <cstring>
#include <iostream>
#include <vector>
using namespace std;#define For(a,begin,end) for(register int a=begin;a<=end;++a)int Row,Column;
const int N=60;
int rooms[N][N];
int color[N][N];
int maxRoomArea=0,roomNo=0;
int roomArea;bool isLeftOpen(int wall,int mask=1){return (wall&mask)==0;}
bool isUpOpen(int wall,int mask=2){return (wall&mask)==0;}
bool isRightOpen(int wall,int mask=4){return (wall&mask)==0;}
bool isDownOpen(int wall,int mask=8){return (wall&mask)==0;}int dfs(int i,int k)
{if(color[i][k]) return 0;++roomArea;color[i][k]=roomNo;if(isLeftOpen(rooms[i][k])) dfs(i,k-1);if(isUpOpen(rooms[i][k])) dfs(i-1,k);if(isRightOpen(rooms[i][k])) dfs(i,k+1);if(isDownOpen(rooms[i][k])) dfs(i+1,k);
}int main()
{cin>>Row>>Column;For(i,1,Row) For(j,1,Column) cin>>rooms[i][j];memset(color,0,sizeof(color));For(i,1,Row) For(j,1,Column){if(!color[i][j]){++roomNo;roomArea=0;dfs(i,j);maxRoomArea=max(maxRoomArea,roomArea);}}cout<<roomNo<<endl;cout<<maxRoomArea<<endl;
}

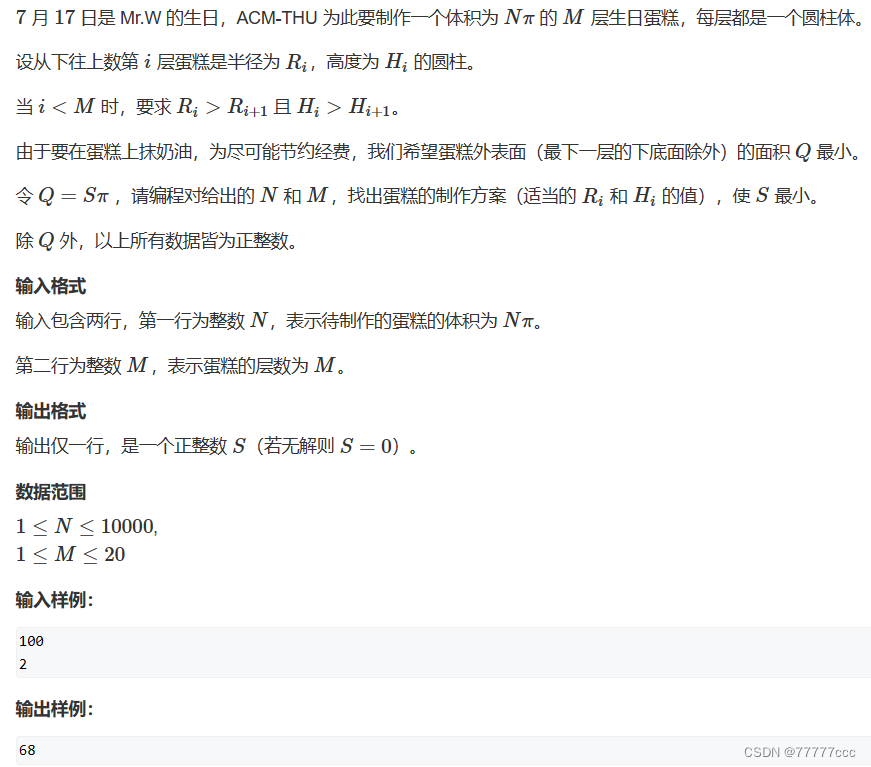
·生日蛋糕

//代码和老师ppt不一样

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;const int N = 25;
int R[N], H[N];
int minv[N], mins[N];//分别表示前1~u层的最小体积和最小侧面积
int n, m, res = 0x3f3f3f3f;void dfs(int u, int v, int s)//当前搜索第u层,u+1~m层的总体积为v,总表面积为s
{if (v + minv[u] > n) return;//体积不合法if (s + mins[u] >= res) return;//表面积一定无法构成更优解if (s + 2 * (n - v) / R[u + 1] >= res) return;//推公式剪枝if (!u)//已经搜完m层了{if (v == n) res = s;//是一个合法解return;}for (int r = min(R[u + 1] - 1, (int)sqrt((n - v) / u)); r >= u; r--)for (int h = min(H[u + 1] - 1, (n - v) / (u * u)); h >= u; h--){R[u] = r, H[u] = h;int t = 0;if (u == m) t = r * r;//如果是最下面那层的话那么算上顶部的表面积之和dfs(u - 1, v + r * r * h, s + 2 * r * h + t);}
}int main()
{cin >> n >> m;for (int i = 1; i <= m; i++)//第i层的最小值就是半径和高都是i{minv[i] = minv[i - 1] + i * i * i;//v = r * r * hmins[i] = mins[i - 1] + 2 * i * i;//s = 2 * r *h}R[m + 1] = H[m + 1] = 0x3f3f3f3f;//哨兵dfs(m, 0, 0);//从最下面那层开始枚举if (res == 0x3f3f3f3f) cout << 0 << endl;else cout << res << endl;return 0;
}

这篇关于校外实训、程序实践--深搜、递归算法的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！