点集的最小覆盖圆求解

最小覆盖圆问题就是给定一个由n个点组成的点集，寻找一个半径最小的圆，将整个点集包围。求解的方法由很多，例如点增量法和三角形增量法。

参考解析几何--最小圆覆盖_牛客博客

点增量法的步骤如下：

下面针对点增量法，用python进行一步一步实现。

首先，先定义点（point）和距离（distance）

class point:def __init__(self, x, y):self.x = xself.y = ydef distance(A, B):return math.sqrt((A.x - B.x)**2 + (A.y - B.y)**2)

一、三点的最小覆盖圆

三点的最小覆盖圆既可能是三点的外接圆，也可能是以其中两个点连线为直径的圆。

三角形外接圆

针对三点组成的三角形，求取其半径及圆心坐标。

def circumcircle(A, B, C):# 防止出现三个点位于一条直线上的情况eps = 0.000000000000000000001a = distance(A, B)b = distance(B, C)c = distance(C, A)r = (a*b*c) / math.sqrt((a+b+c) * (-a+b+c) * (a-b+c) * (a+b-c) + eps)# 计算外心坐标a1 = 2*(A.x - B.x)b1 = 2*(A.y - B.y)a2 = 2*(B.x - C.x)b2 = 2*(B.y - C.y)c1 = A.x**2 - B.x**2 + A.y**2 - B.y**2c2 = B.x**2 - C.x**2 + B.y**2 - C.y**2x = (b2*c1 - b1*c2) / (a1*b2 - a2*b1 + eps)y = (-a2*c1 + a1*c2) / (a1*b2 - a2*b1 + eps)circum_point = point(x, y)results = [r, circum_point]return results

以其中两个点连线为直径的覆盖圆

以两点连线为直径的圆作为覆盖圆的充要条件是，第三个点在该圆内。否则，这个圆就不能作为覆盖圆，就无需与三点的外接圆进行比较是否是最小覆盖圆。

def twoPointCircle(A, B, C):""":param A: 点1:param B: 点2:param C: 直线AB外一点C:return: 如果点C在以AB为直径的圆内，则返回半径和圆心，否则返回-1"""centerPoint = point((A.x+B.x)/2, (A.y+B.y)/2)r = distance(A, B) / 2d = distance(C, centerPoint)if d <= r:results = [r, centerPoint]else:results = [-1, centerPoint]return results

求取三点的最小覆盖圆

比较外接圆和以其中两个点连线为直径的覆盖圆的半径，取最小半径的作为最小覆盖圆。

# 找三点中最小覆盖圆
def minCircle(A, B, C):# 外接圆circum_results = circumcircle(A, B, C)# 以其中两点为直径的圆AB_results = twoPointCircle(A, B, C)BC_results = twoPointCircle(B, C, A)CA_results = twoPointCircle(C, A, B)circleOfTwoPoint = [AB_results, BC_results, CA_results]min_r = circum_results[0]min_circle_point = circum_results[1]for result in circleOfTwoPoint:if result[0] == -1:continueelse:if result[0] < min_r:min_r = result[0]min_circle_point = result[1]return min_r, min_circle_point

二、四个点的最小覆盖圆

在求取了ABC三点的最小覆盖圆以后，若 点集 中距离该最小覆盖圆圆心最远的点D不在圆内，那么根据步骤（4），需要在这四个点中找到其中三个点的最小覆盖圆，使其包含这四个点，且半径最小。

寻找点集中距离ABC三点最小覆盖圆的点D

暴力搜索

def findLongestPoint(pointSet, centralPoint):d = 0longestPoint = Nonefor p in pointSet:d_p = distance(p, centralPoint)if d_p >= d:longestPoint = pd = d_preturn longestPoint

判断点D是否在ABC三点的最小覆盖圆中

def isInMinCircle(A, B, C, D):min_r, min_circle_point = minCircle(A, B, C)d = distance(D, min_circle_point)if d > min_r:results = [0, min_r, A, B, C]else:results = [1, min_r, A, B, C]return results

在ABCD四点中寻找新的ABC三点，生成四点最小覆盖圆

def findNewThreePoint(A, B, C, D):ABD_results = isInMinCircle(A, B, D, C)ACD_results = isInMinCircle(A, C, D, B)BCD_results = isInMinCircle(B, C, D, A)results = [ABD_results, ACD_results, BCD_results]# 较大的数值min_r = 100000000for result in results:if result[0] == 0:continueelse:if result[1] <= min_r:A = result[2]B = result[3]C = result[4]return A, B, C

三、实验验证

点集

使用包含二十个点的点集对算法进行验证，寻找其最小覆盖圆。

画图

def plt_circle(pointSet, min_circle_point, min_r, isCircum=False):# 所有点positionPointSet = np.array([[-7.590, 0.796],[-7.601, 0.796],[-7.603, 0.797],[-7.592, 0.796],[-7.591, 0.788],[-7.592, 0.794],[-7.587, 0.794],[-7.587, 0.789],[-7.590, 0.792],[-7.588, 0.798],[-7.596, 0.794],[-7.606, 0.797],[-7.607, 0.795],[-7.609, 0.797],[-7.610, 0.798],[-7.610, 0.790],[-7.607, 0.791],[-7.610, 0.797],[-7.605, 0.796],[-7.604, 0.791]])pointSets = []for p in positionPoint:pointSets.append(point(p[0], p[1]))# 画出所有的点plt.plot(positionPointSet[:, 0], positionPointSet[:, 1], "go", label="point set")# 最远点D = findLongestPoint(pointSets, min_circle_point)plt.plot(D.x, D.y, "ys", label="most far point")# 画三点positionPoints = []for p in pointSet:positionPoints.append([p.x, p.y])positionPoints = np.array(positionPoints)plt.plot(positionPoints[:, 0], positionPoints[:, 1], "r*", label="calcu points")# 画圆心plt.plot(min_circle_point.x, min_circle_point.y, "kx", label="min circle central point")# 画圆theta = np.arange(-math.pi, math.pi, 2*math.pi/1000)x_circle = [min_circle_point.x + min_r * math.cos(t) for t in theta]y_circle = [min_circle_point.y + min_r * math.sin(t) for t in theta]plt.plot(x_circle, y_circle, label="min circle")if isCircum:result = circumcircle(pointSet[0], pointSet[1], pointSet[2])x_circumcircle = [result[1].x + result[0] * math.cos(t) for t in theta]y_circumcircle = [result[1].y + result[0] * math.sin(t) for t in theta]plt.plot(x_circumcircle, y_circumcircle, label="circumcircle")plt.legend()plt.axis("equal")plt.grid()plt.show()

测试代码

if __name__ == "__main__":eps = 0.0000001pointSet = []positionPoint = np.array([[-7.590, 0.796],[-7.601, 0.796],[-7.603, 0.797],[-7.592, 0.796],[-7.591, 0.788],[-7.592, 0.794],[-7.587, 0.794],[-7.587, 0.789],[-7.590, 0.792],[-7.588, 0.798],[-7.596, 0.794],[-7.606, 0.797],[-7.607, 0.795],[-7.609, 0.797],[-7.610, 0.798],[-7.610, 0.790],[-7.607, 0.791],[-7.610, 0.797],[-7.605, 0.796],[-7.604, 0.791]])for p in positionPoint:pointSet.append(point(p[0], p[1]))A = pointSet[0]B = pointSet[1]C = pointSet[2]min_r, min_circle_point = minCircle(A, B, C)plt_circle([A, B, C], min_circle_point, min_r, isCircum=True)D = findLongestPoint(pointSet, min_circle_point)while distance(D, min_circle_point) - min_r > eps:A, B, C = findNewThreePoint(A, B, C, D)min_r, min_circle_point = minCircle(A, B, C)plt_circle([A, B, C], min_circle_point, min_r, isCircum=True)D = findLongestPoint(pointSet, min_circle_point)print(min_r)print("X: {0} | Y: {1}".format(min_circle_point.x, min_circle_point.y))

结果

第一次迭代结果

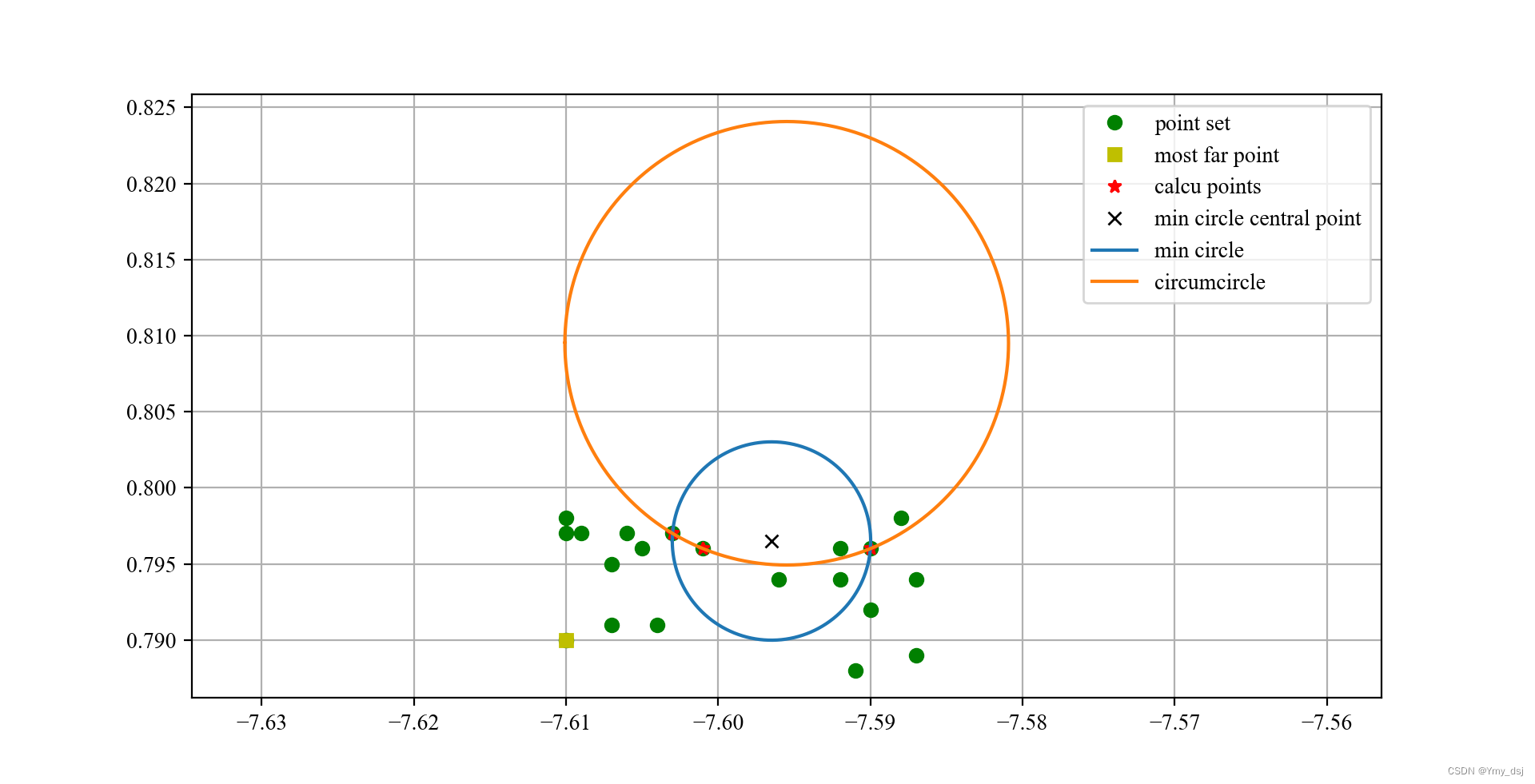
 第二次迭代结果

 第三次迭代结果

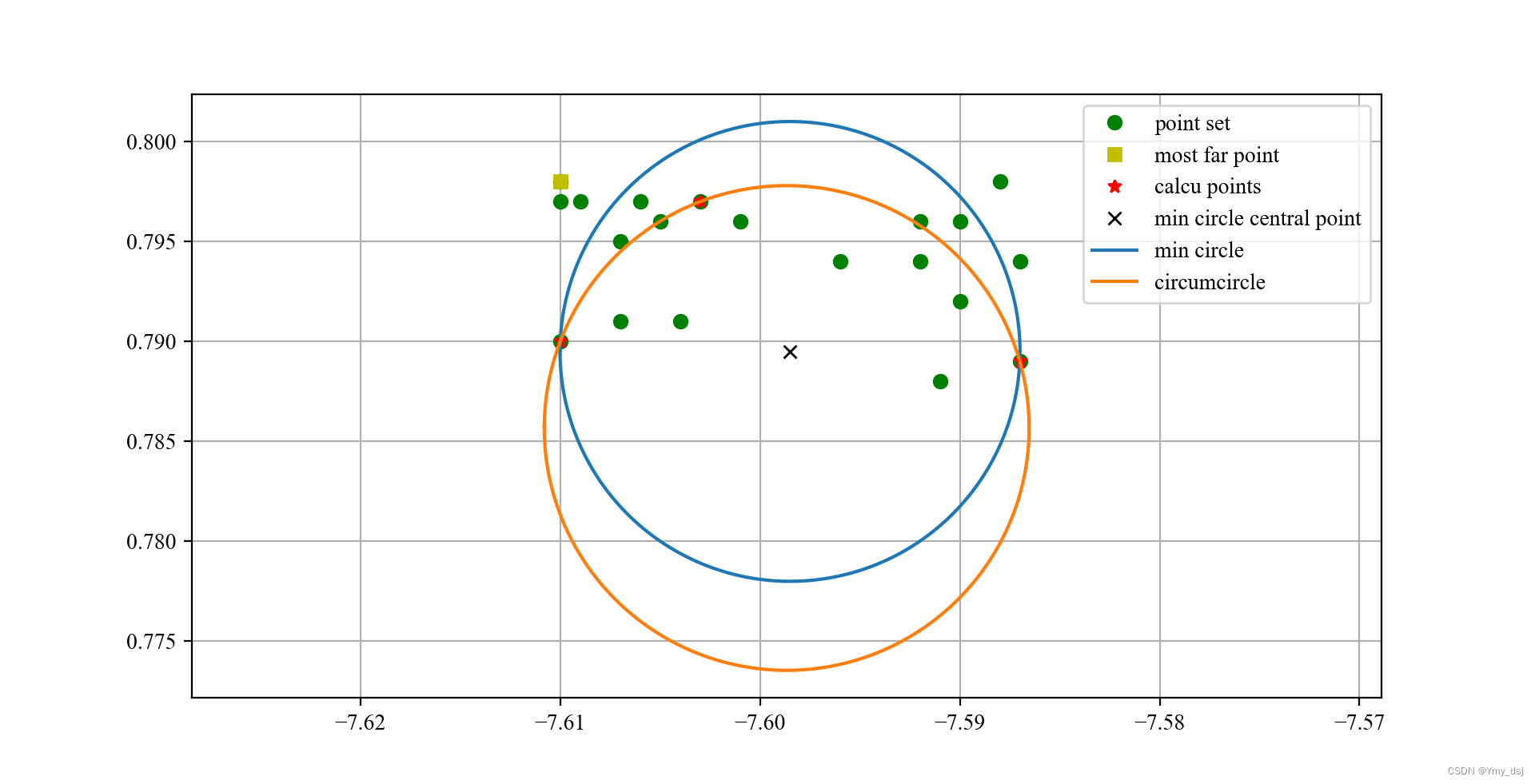
第四次迭代结果

 经过四次迭代之后，找到了点集的最小覆盖圆，输出半径和圆心结果。

0.012349089035228739
X: -7.5985 | Y: 0.7935000000000001