Dijkstra算法——单源最短路径（指定一个节点（源点）到其余各个顶点的最短路径）

1.预设场景

国庆期间，小明打算从1号城市出发，在五天假期中分别去往不同的城市（2，3，4，5，6）旅游，为减轻负担，他想要知道1号城市到各个城市之间的最短距离。

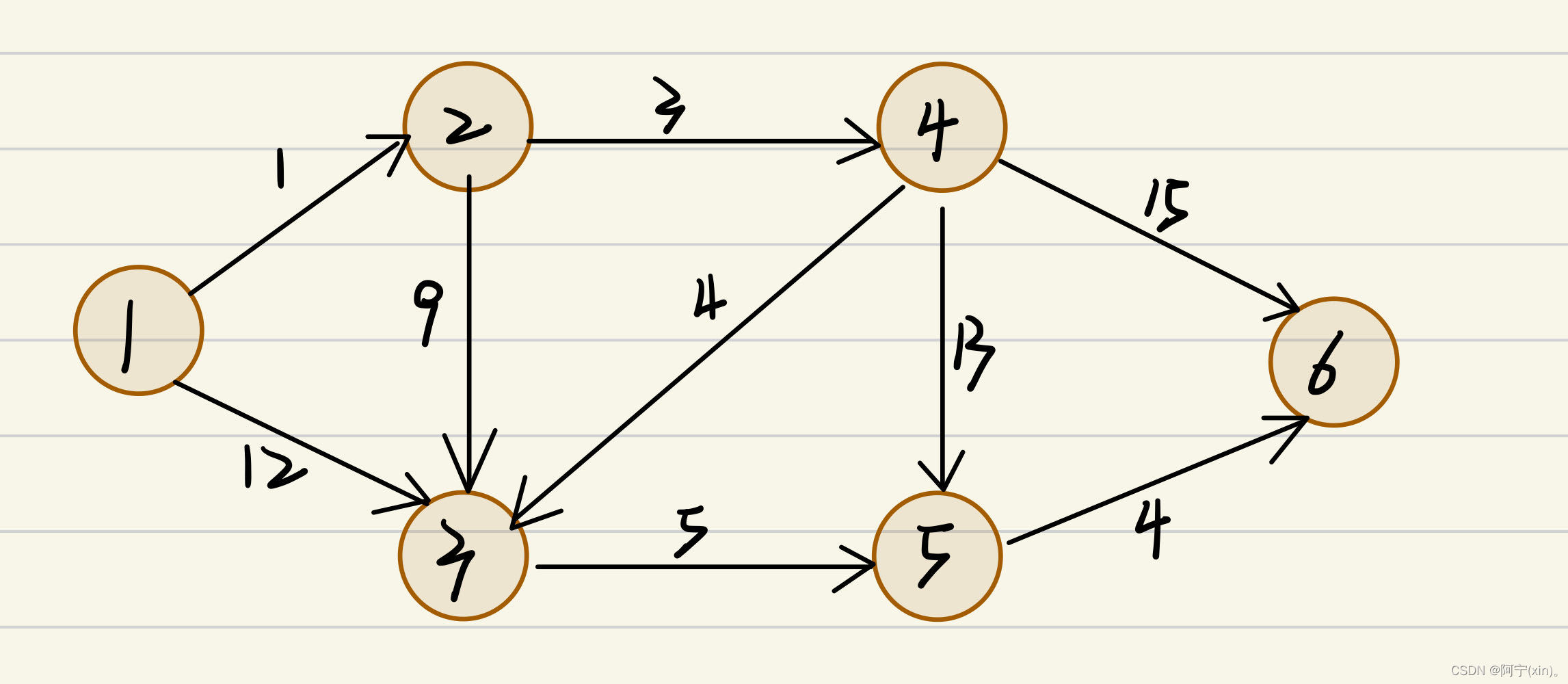
现在需要设计一种算法求得源点到任意一个城市之间的最短路径。该问题的求解也被称为“单源最短路径”。

2.数据结构描述

在所有的数据结构中，0号下标（0行0列）均不存储元素
同样，这里使用二维数组e来存储顶点之间边的关系。初始值如下：

用一个一维数组dis存储源点（1号顶点）到其余各个顶点的初始距离。其初始值如下：

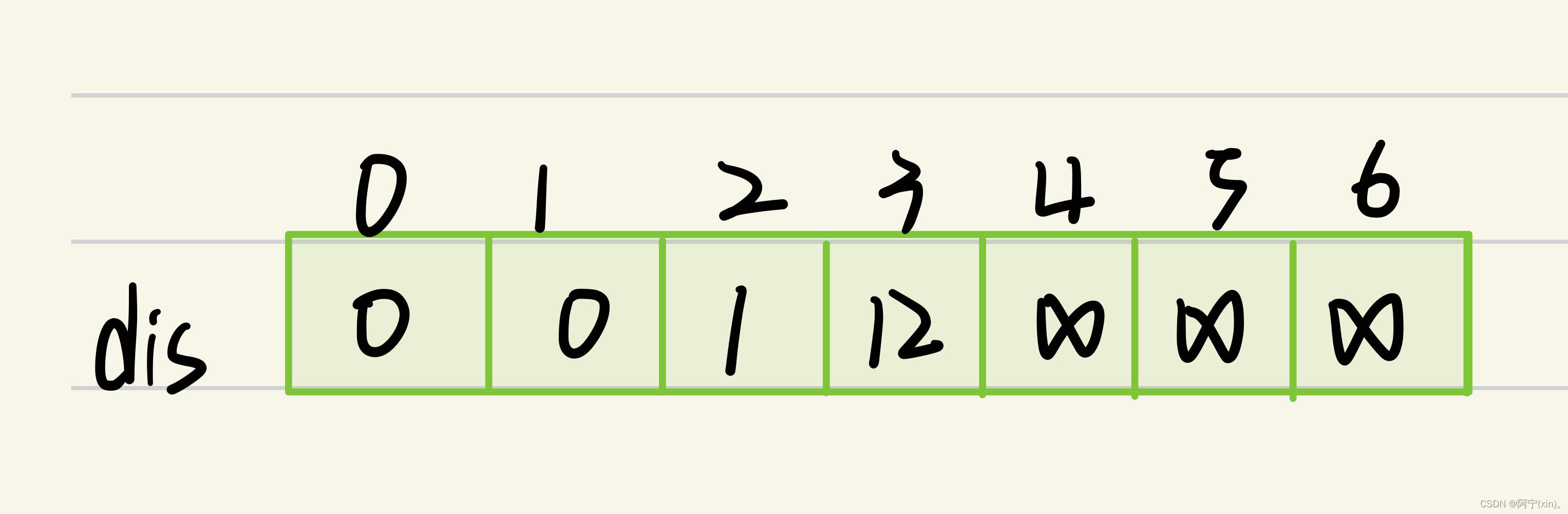
3.算法基本思想

算法的基本思想是：每次找到距离源点最近的一个节点，然后以该节点为中心进行扩展，最终得到源点到其余所有点的最短路径。具体步骤如下：

1. 将所有的顶点分为两部分：已知最短路径的顶点集合P和未知最短路径的顶点集合Q。开始，已知最短路径的顶点集合P中只有源点一个节点，知最短路径的顶点集合Q中包含了除了源点之外的所有节点。为减少空间复杂度（P和Q不重新开辟空间），用一个数组book记录那个节点在P中，那个节点在Q中。例如对于节点i来说，book[i] = 1表示节点i在集合p中，book[i] = 0表示节点i在集合Q中。
2. 设置源点i到自己的最短路径为0，即dis[i] = 0。若存在有源点能直接到达的顶点j，则把dis[j] = e[i][j]，同时把其他源点不能直接到达顶点的最短路径设为∞。
3. 在集合Q的所有顶点中选择一个离源点i最近的顶点u（dis[u]最小）加入到集合P。然后考察所有以u为起点的边，对每一条边进行松弛操作。（何为松弛操作：例如存在一条从u到j的边，那么就可以以u为中间节点到达j，这条路径的长度是e[u][j] + dis[u]，如果这个值比目前的dis[j]小，可以就找到了一个i到j的最短路径，用新值代替当前dis[j]中的值。）
4. 重复步骤3，直至集合Q为空。最终数组dis中的值就是源点到所有顶点的最短路径。

具体过程详解

还是以下面的图为例：

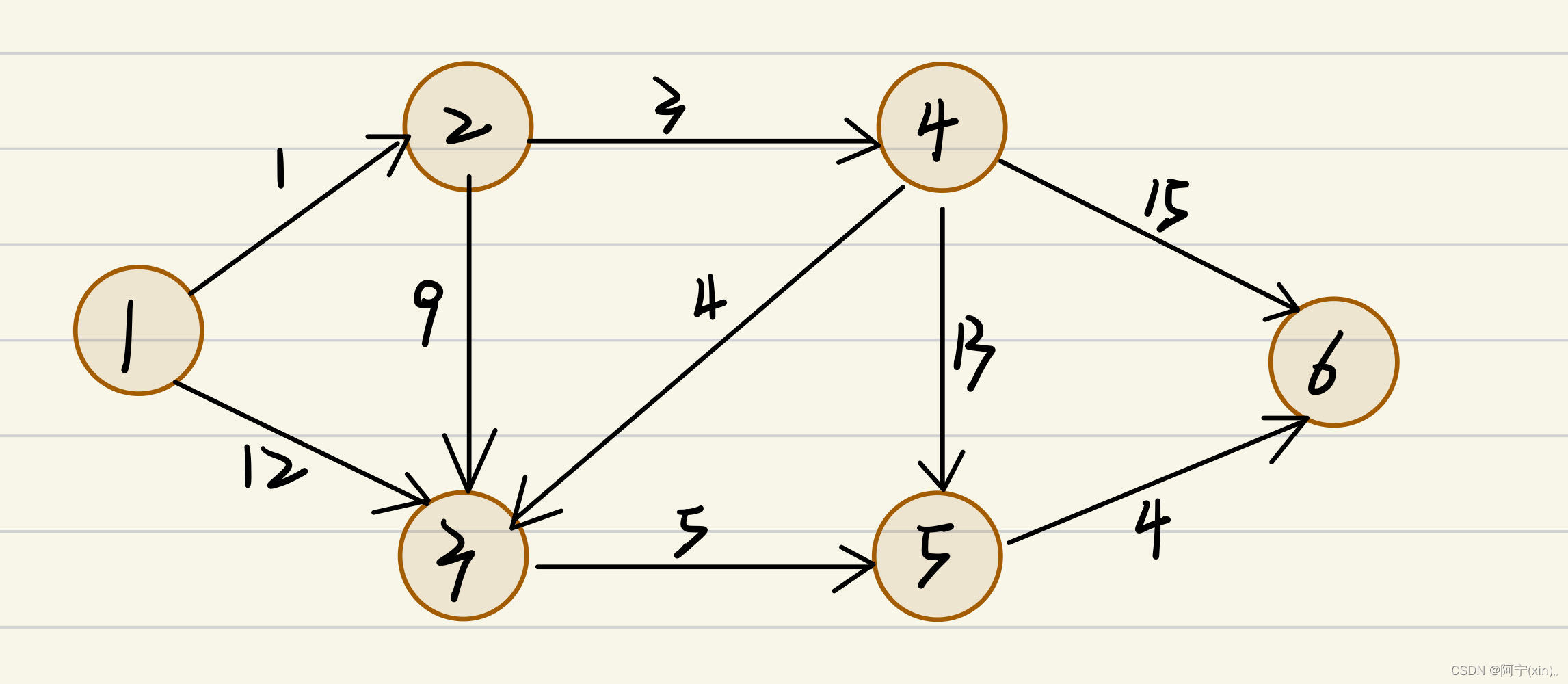
，其初始化二维数组e和数组dis皆如上所示，没有任何变化。

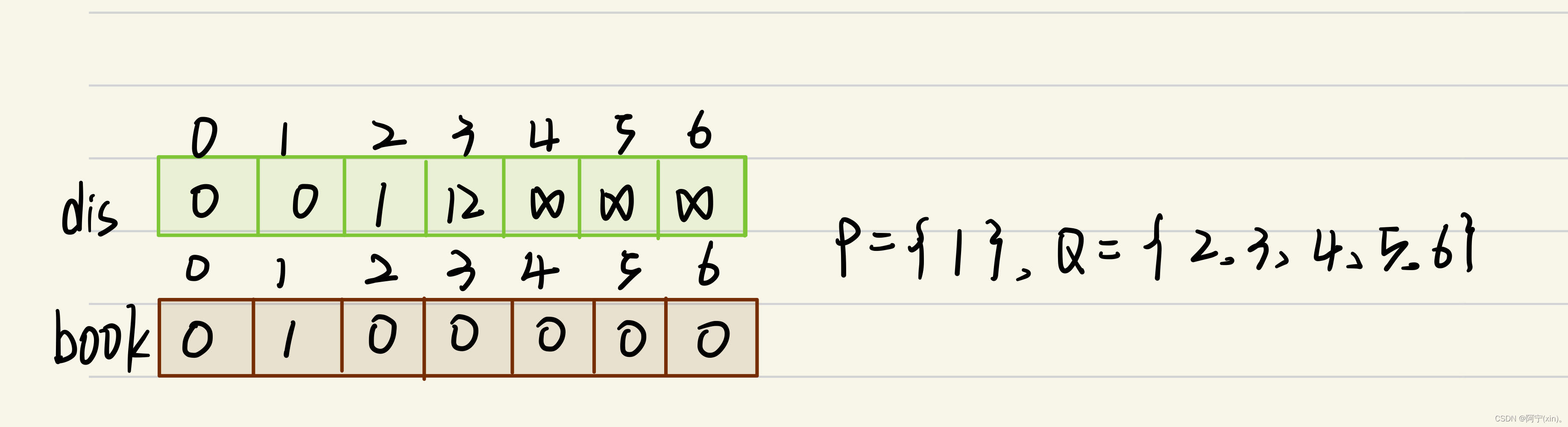
具体步骤如下：

1. 初始化e[vertice + 1][vertice + 1]，book[vertice + 1]（集合P和集合Q），和dis[vertice + 1]（如上所示）。

2. 观察比较数组dis，可以得到dis[2]为数组dis中的最小值，而且book[2]==0。所以选择2号节点。对儿2号节点来说，有e[2][3] = 9和e[2][4] = 3。即从2号节点出发可以到达3，4号两个节点。
   ①dis[3]==12 >(dis[2] + e[2][3] == 10)，所以可以判断1号顶点->3号顶点（dis[3]）的距离 大于 1号顶点->2号顶点->3号顶点，于是更新dis[3]的值。
   ②dis[4]==∞ >(dis[2] + e[2][4] == 4)，所以可以判断1号顶点->4号顶点（dis[3]）的距离 大于 1号顶点->2号顶点->4号顶点，于是更新dis[3]的值。
   至此，以2号节点的边来“松弛”过程结束，数据结构变化如下：
   

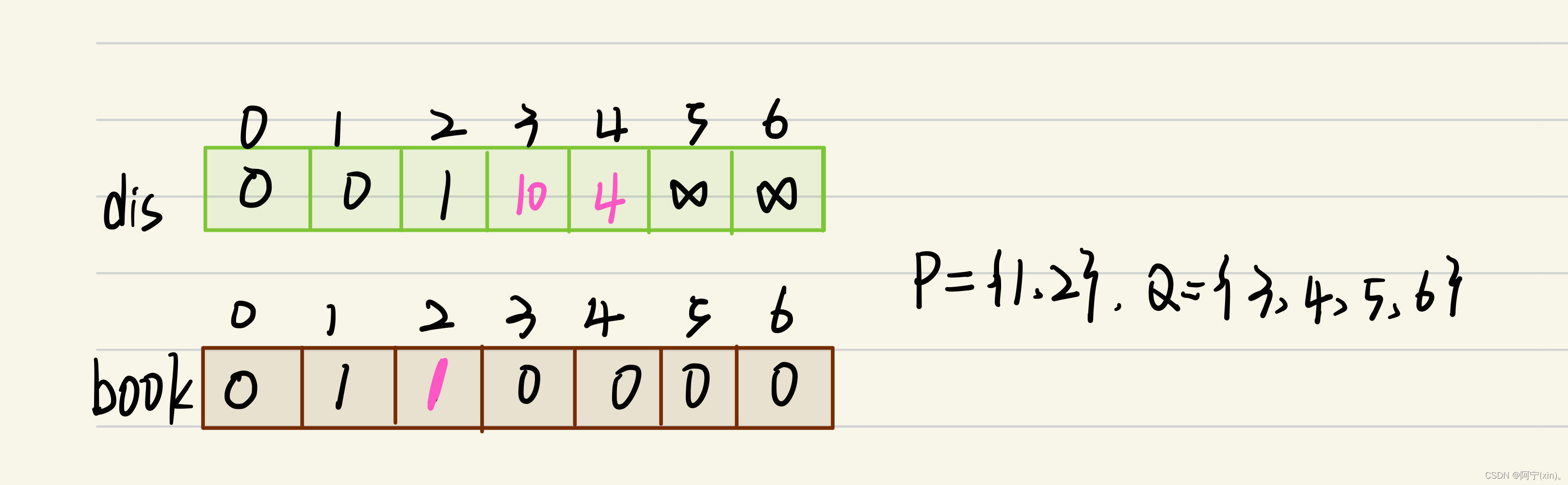
3. 观察步骤2后的结果，可以发现dis[4]为数组dis中的最小值，而且book[4]==0。所以选择4号节点。对儿4号节点来说，有e[4][3] = 4、e[4][5] =13和e[4][6] = 15。即从4号节点出发可以到达3，5，6号三个节点。
   ①dis[3]==10 >(dis[4] + e[4][3] == 8)，所以可以判断1号顶点->2号顶点->3号顶点（dis[3]）的距离 大于 1号顶点->2号顶点->4号顶点->3号顶点，于是更新dis[3]的值。（2号顶点为上一次的更新过程）
   ②dis[5]==∞ >(dis[4] + e[4][5] == 17)，所以可以判断1号顶点->5号顶点（dis[5]）的距离 大于 1号顶点->4号顶点->5号顶点，于是更新dis[5]的值。
   ③dis[6]==∞ >(dis[4] + e[4][6] == 19)，所以可以判断1号顶点->6号顶点（dis[6]）的距离 大于 1号顶点->4号顶点->6号顶点，于是更新dis[6]的值。
   至此，以4号节点的边来“松弛”过程结束，数据结构变化如下：
   
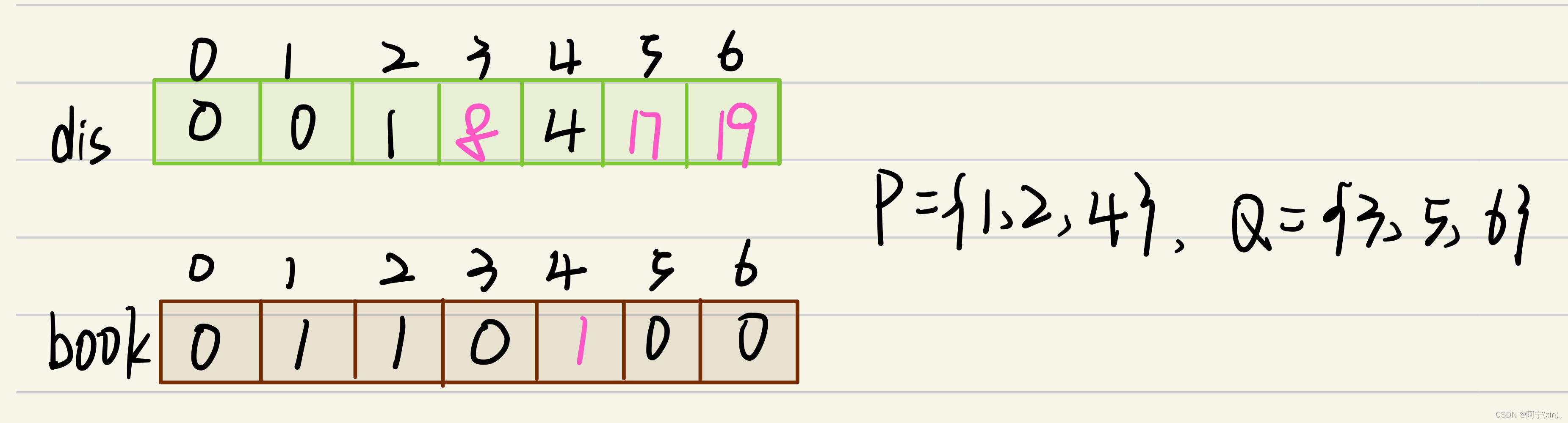
   4.观察步骤3后的结果，可以发现dis[3]为数组dis中的最小值，而且book[3]==0。所以选择3号节点。对儿3号节点来说，有e[3][5] = 5。即从3号节点出发可以到达5号节点。
   ①dis[5]==17 >(dis[3] + e[3][5] == 13)，所以可以判断1号顶点->2号顶点->4号顶点->5号顶点（dis[5]）的距离 大于 1号顶点->3号顶点->5号顶点，于是更新dis[3]的值。（2,4号顶点为上一次的更新过程）
   至此，以3号节点的边来“松弛”过程结束，数据结构变化如下：
   
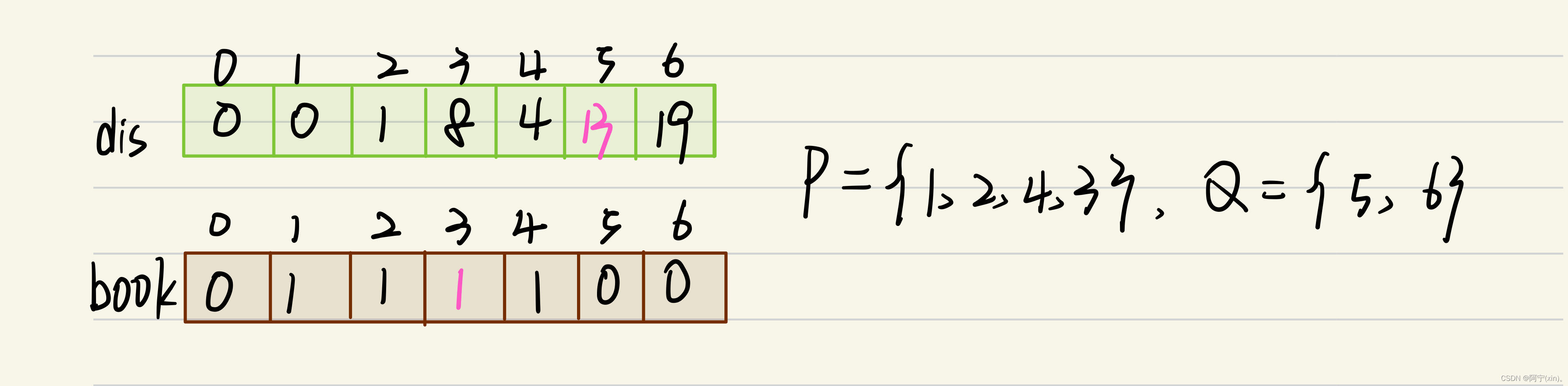
   5.观察步骤4后的结果，可以发现dis[5]为数组dis中的最小值，而且book[5]==0。所以选择5号节点为中间节点。对儿4号节点来说，有e[5][6] = 4。即从5号节点出发可以到达6号节点。
   ①dis[6]==19 >(dis[5] + e[5][6] == 17)，所以可以判断1号顶点->2号顶点->4号顶点->6号顶点（dis[6]）的距离 大于 1号顶点->2号顶点->4号顶点->3号顶点->5号顶点->6号顶点，于是更新dis[6]的值。（2,4号顶点为上一次的更新过程）
   至此，以5号节点的边来“松弛”过程结束，数据结构变化如下：
   
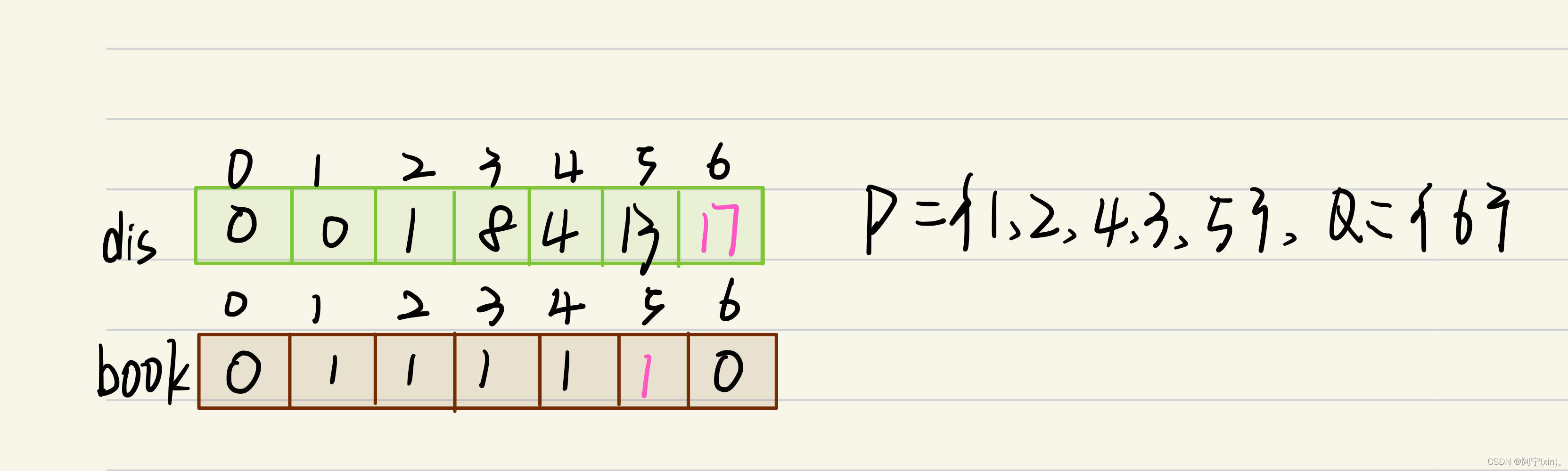
   6.观察步骤5后的结果，可以发现dis[6]为数组dis中的最小值，而且book[6]==0。所以选择6号节点为中间节点。但是对于6号节点来说，没有可以扩展的节点。
   至此，以6号节点的边来“松弛”过程结束，数据结构变化如下：
   
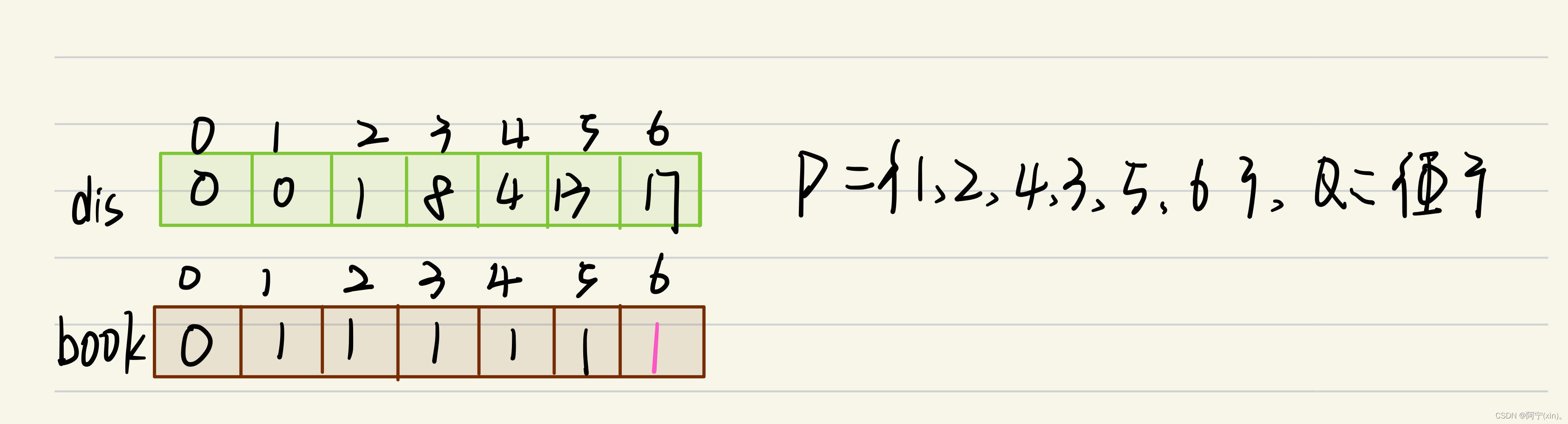
   最后，数组dis如下，这便是1号顶点到其余顶点之间的最短距离：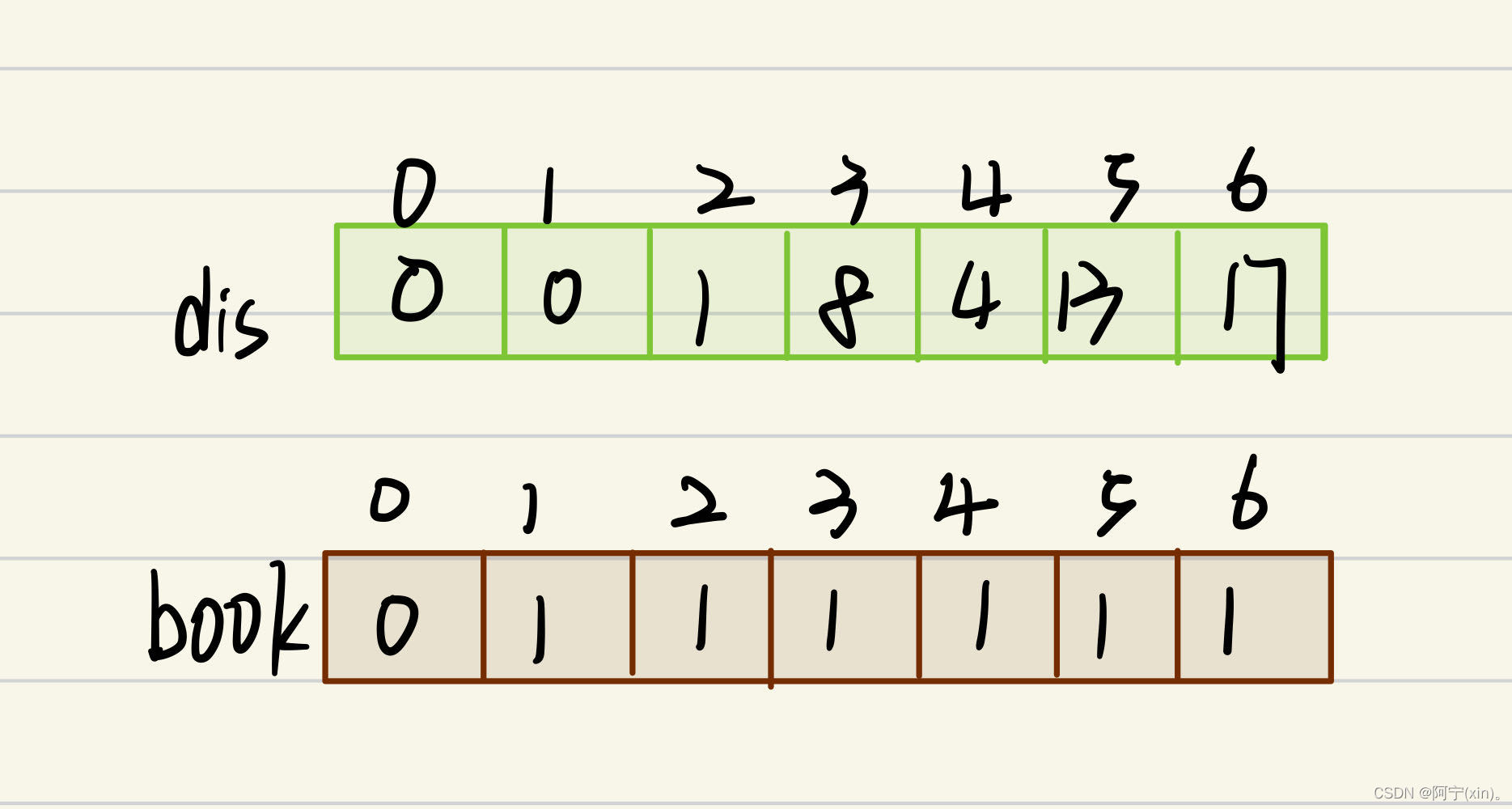

4.代码实现

#include <vector>
#include <iostream>using namespace std;class Digkstra
{
private:int vertice = 0;//顶点数int edge = 0;//边数vector<vector<int>> e;vector<bool> book;//判断顶点j是否扩展过vector<int> dis;//源点到各个顶点之间的最短距离public:Digkstra(int x, int y) :vertice(x), edge(y){//图的初始化从下标1开始e.resize(vertice + 1);//初始化二维数组的行for (int i = 0; i <= vertice; i++){e[i].resize(vertice + 1);//初始化二维数组的列}dis.resize(vertice + 1);book.resize(vertice + 1);}//图的初始化void Init_Digkstra(){for (int i = 0;i <= vertice; i++){for (int j = 0; j <= vertice; j++){if (i == 0 || j == 0){e[i][j] = 0;}if (i == j){e[i][j] = 0;}else{e[i][j] = INT_MAX;}}}}//读入图的边，并且根据边的信息初始化数组dis，数组bookvoid GetEdgeInfo(){cout << "输入边的信息（节点1，节点2，权重）：" << endl;int e1 = 0, e2 = 0, weigth = 0;for (int i = 1; i <= edge; i++){cin >> e1 >> e2 >> weigth;e[e1][e2] = weigth;}for (int i = 1; i <= vertice; i++){dis[i] = e[1][i];}book[1] = true;}//打印void Print(){for (int i = 1; i <= vertice; i++){cout << dis[i] << "    "; }         cout << endl;}//Digkstra核心思想void Digkstra_Alg(){int u = 0;//离1号顶点最近顶点的下标for (int k = 1; k <= vertice; k++){int min = INT_MAX;//找离1号节点最近的节点（找数组dis中的最小值）           for (int j = 1; j <= vertice; j++){if (book[j] == false && dis[j] < min){min = dis[j];u = j;}}book[u] = true;for (int i = 1; i <= vertice; i++){if (e[u][i] < INT_MAX){if (dis[i] > dis[u] + e[u][i]){dis[i] = dis[u] + e[u][i];}}}}}};int main()
{Digkstra Digkstra(6, 9);Digkstra.Init_Digkstra();Digkstra.GetEdgeInfo();cout << "初始信息：" << endl;Digkstra.Print();Digkstra.Digkstra_Alg();cout << "单源最短路径(顶点1到其余各顶点)：" << endl;Digkstra.Print();return 0;
}

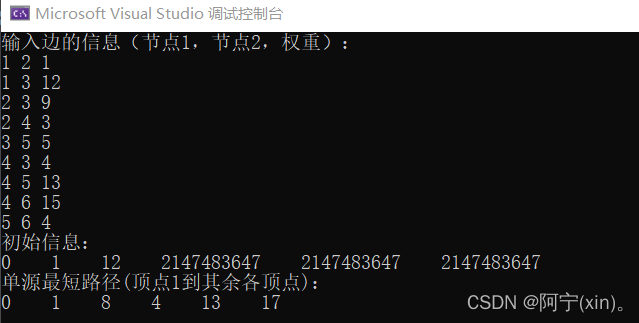
5.总结

通过代码，可以得到该算法的时间复杂度是O(N^2)。而且这是一种基于贪心策略的算法。每次扩展一个新的最短距离的节点，就要更新与其相邻的点的距离。当所有边权重为正时，由于不存在一个路程更短的没有被扩展的点，所以这个点的距离不会别再次改变，从而保证了算法的正确性。
根据这一特点，用此算法求最短路径的图是不能有负权重的，因为扩展到负权重边的时候会产生更短的距离，有可能破坏已经更新的点距离不会改变的性质。

6.END！