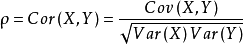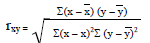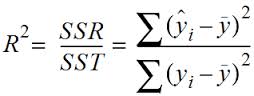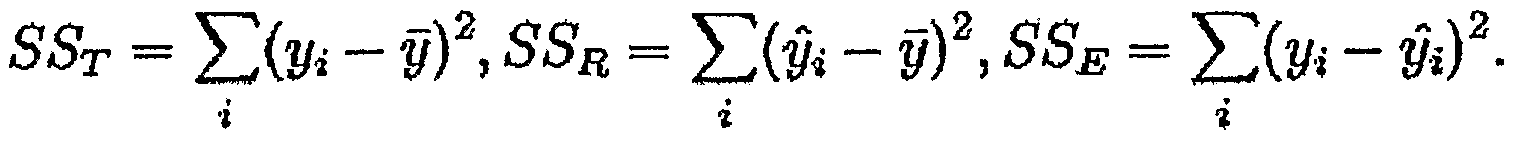【机器学习】9.回归中的线性度和决定系数

本文主要是介绍【机器学习】9.回归中的线性度和决定系数，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1.皮尔逊相关系数

1.1衡量两个值线性相关强度的量

1.2取值范围：[-1,+1]

正相关：>0，负相关：<0，不相关：=0。

1.3

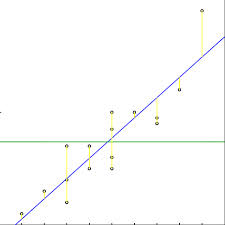
2.例子

3.R平方值

3.1定义：决定系数，反映因变量的全部变异能通过回归关系对自变量解释的比例。

3.2描述：如R平方为0.8，则表示回归关系可以解释因变量80%的变异。即如果我们能控制自变量不变，则因变量的变异程度会减少80%。

3.3简单线性回归：R^2=r*r

多元线性回归：

式子的意思是在整体y的变换中，能由模型解释的y的变换的比例

SSE+SSR=SST （SSE值误差量）

4.R平方也有其局限性，R平方随着自变量的增加会变大，R平方和样本量是有关系的。因此为了抵消样本量对R平方的影响，我们要对R平方进行修正，修正的方法：

5.python实现

# -*- coding: utf-8 -*-
import numpy as np
from astropy.units import Ybarn
import math#相关性计算
def computerCorrelation(X,Y):xBar=np.mean(X)yBar=np.mean(Y)SSR=0varX=0varY=0for i in range(0,len(X)):diffXXBar=X[i]-xBardiffYYBar=Y[i]-yBarSSR+=(diffXXBar*diffYYBar)varX+=diffXXBar**2varY+=diffYYBar**2SST=math.sqrt(varX*varY)return SSR/SST
####决定系数计算
def polyfit(x,y,degree):results={}coeffs=np.polyfit(x,y,degree)           #传入自变量x,因变量y，线性回归最高次项次数，自动算回归方程 相关系数b0,b1,b2.。。results['polynomial']=coeffs.tolist()p=np.poly1d(coeffs)                     #回归线yhat=p(x)ybar=np.sum(y)/len(y)ssreg=np.sum((yhat-ybar)**2)print"ssreg:",str(ssreg)sstot=np.sum((y-ybar)**2)print"sstot",str(sstot)results['determination']=ssreg/sstotprint"results",resultsreturn results
##testX=[1,3,8,7,9]
testY=[10,12,24,21,34]print"r:",computerCorrelation(testX, testY)
print"r^2:",str(computerCorrelation(testX, testY)**2)
print polyfit(testX, testY, 1)