非静压模型NHWAVE学习（2）——垂向σ-坐标系

这个系列的blog有点类似NHWAVE手册和代码的解读，内容之中也会穿插一些个人的学习体会。

NHWAVE模型原理回顾

在 非静压模型NHWAVE学习（1）——模型原理简介 中，我们主要介绍了模型的控制方程。
包括控制水流运动的N-S方程，和控制物质输运的对流-扩散方程。

1. N-S方程
   
2. 对流-扩散方程
   

垂向σ-坐标系

在非静压模型NHWAVE中，自由表面水位 η 被假定为水平位置的单值函数，即
$$\eta =\eta (x,y,t)$$
这种处理方式不同于传统的VOF、MAC等自由表面追踪技术，有着更高的计算效率。

为了使模型系统适应上述的处理方式，以及网格适应复杂的水底地形与自由表面形态的变化，NHWAVE模型采用了Phillips (1957) ¹ 提出的坐标变换方法（将在原时空笛卡尔坐标系统(x*, y*, z*, t*)下的物理量转化至新系统(x, y, z, t)之中）：

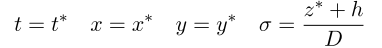
式子中，D = h + η，h表示水深，η表示水位；于是，在垂直方向上，取值范围为 [-h(x*, y*, t*), η(x*, y*, t*)] 的 z*(x*, y*, t*) 转换成了处处取值为 [0, 1] 的 σ。就像方程做了如下的网格变形。

（注： 上图中左图为物理区域，右图为转化后的计算区域）

基于σ-坐标系的N-S方程的变形

假设一个在新坐标系统下的函数
$$f=f(x^{\ast },y^{\ast },z^{\ast },t^{\ast })$$
应用复合函数的链式法则，我们可以得到：

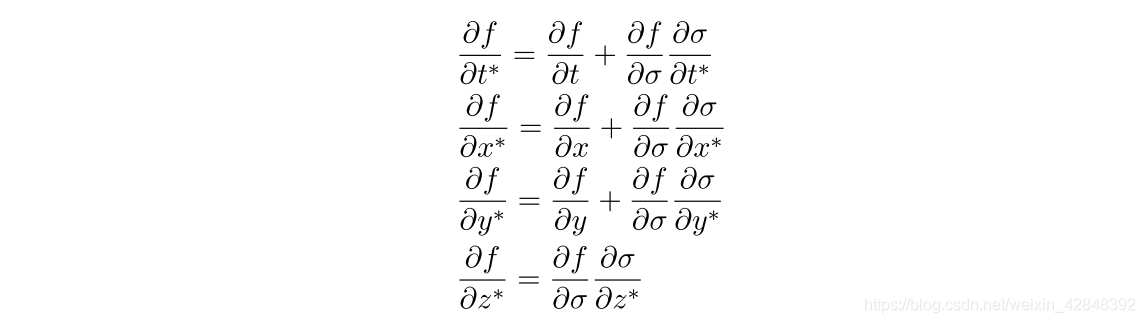
以及，

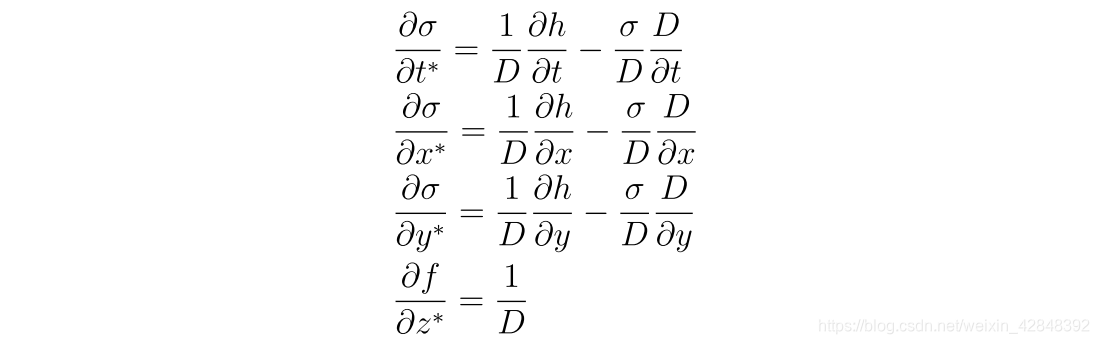
于是，连续性方程就被写成

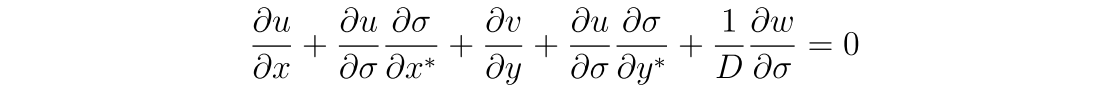
或

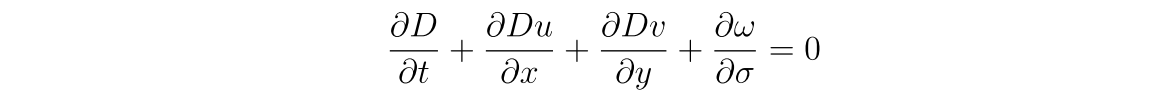
式子中的ω表示的是σ-坐标系下的垂向速度（垂直于σ-坐标系网格的速度），ω与垂向速度w的关系为：

将上述连续性方程沿垂向积分，得到了

解出了总水深D，则可求得自由表面位置；即上式是自由表面的控制方程。

同理，N-S方程中的动量方程同样可以由上面的方法进行坐标变换，得到如下的动量方程形式：

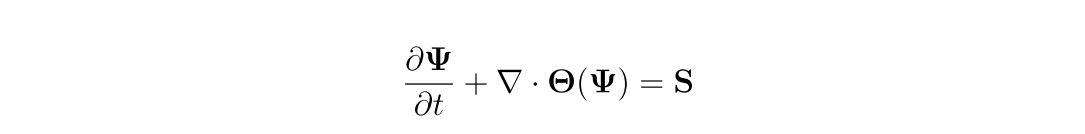
其中，



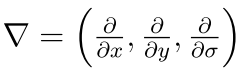
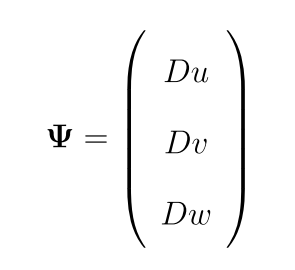
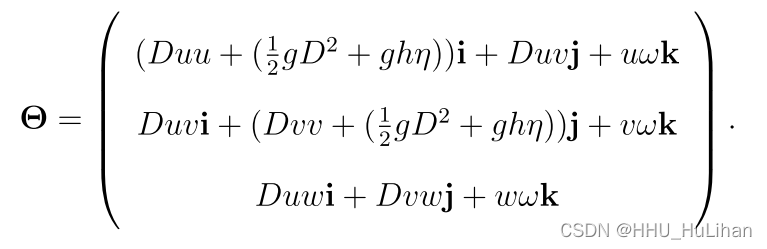
详细可见NHWAVE模型手册及Gangfeng Ma等人的论文（2012²，2013 ³）。

其它

最后再简要介绍以下其它常见的σ-坐标系。

NHWAVE模型中的σ-坐标系一般被称作单层σ-坐标系，即它将整个垂向区域都纳入了σ-坐标体系中。在实际应用过程中，单层σ-坐标系内整个计算区域的网格会随着自由水面波动而波动，难以固定计算域内某一固定点的位置。
为了克服这样的缺陷，香港学者李行伟（C. W. Lee）等人提出了两层σ-坐标系 ⁴，即上层网格随自由水面波动而变化，下层网格固定不变。他应用这种坐标系计算了底柱扰流，得到了非常不错的模拟效果。
在此之后，我国学者林鹏智（P. Lin）提出了多层σ-坐标系⁵，并将此推广到任意层 坐标下波和障碍物耦合作用研究。以三层σ-坐标系为例，它在垂向的网格布置如下图所示。

（注： 上图中左图为物理区域，右图为转化后的计算区域）

参考文献