在 Python 中逐步构建 DCF（贴现流）估值

 执行安装软件：

pip install compdata

1. 业务理解

        DCF是啥？用于生成贴现现金流(dcf)的 Python 库。提供了典型的银行业务方法，如插值、复利、贴现和外汇。

让我们应用DCF方法对截至31年2020月<>日（以下简称“估值日期”）的以色列系统与应用公司（以下简称“公司”）进行估值。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from datetime import datetime 
start_time = datetime.now() 
from datetime import datetime
# datetime object containing current date and time
now = datetime.now()
dt_string = now.strftime(“%d/%m/%Y %H:%M:%S”)
%matplotlib inline 

1.1. 估价方法

有几种常用的估值方法。每种方法有时在使用理论上可能比其他方法更合理。特定方法的合理性完全取决于每个个案所涉及的相对情况。

普遍接受的估值方法通常如下：

• 市场方法;
• 收入法;
• 基于资产的方法。

在每个类别中，存在各种方法来帮助估计公允价值。以下各节简要概述了每种方法的理论基础，并讨论了与所执行分析相关的具体方法。

市场方法

        市场办法是指被估价企业股权的实际交易或在公开市场上交易的类似企业的交易。企业股权中的第三方交易，如果以公平交易的方式进行，一般是公允市场价值的最佳估计。

        在使用来自类似企业的交易时，有两种主要方法。第一种通常称为准则交易法，涉及从具有相似财务和经营特征的企业的销售中确定估值倍数，并将这些倍数应用于目标企业。

        第二种，通常被称为指南上市公司方法，涉及识别和选择与被估值企业具有相似的财务和经营特征的上市公司。一旦确定了公开交易的企业，就可以得出估值倍数，调整可比性，然后应用于标的企业，以估计其股权或投资资本的价值。

收入法

        收益法的前提是，证券或资产的价值是可用于分配给证券或资产投资者的未来盈利能力的现值。收入法下常用的方法是贴现现金流量分析。

        贴现现金流分析涉及预测适当时期内的适当现金流，然后以适当的贴现率将其折现回现值。该贴现率应考虑货币的时间价值、通货膨胀以及资产所有权或被估值的担保权益所固有的风险。

基于资产的方法

        第三种估值方法是基于资产的方法。使用基于资产的方法对资产进行离散估值是基于置换作为价值指标的概念。

        谨慎的投资者不会为资产支付超过他或她可以替换资产的金额。基于资产的方法根据复制或更换财产的成本确定价值，减去物理退化和功能过时的折旧（如果存在和可衡量）。

        这种方法通常为土地改良、特殊用途建筑、特殊结构、系统和特殊机械设备的价值提供最可靠的指示。在三种估值方法中，从概念角度来看，基于资产的方法通常被认为是最薄弱的。

1.2. 选择的方法

        为了评估公司的价值，我必须确定其总投资资本的价值（请注意，投资资本和股权价值这两个术语在本文中可以互换使用）。在为公司制定价值结论时，我依靠收入法。

        没有使用市场方法的指南上市公司方法，因为没有一家指南公司被确定为与公司直接可比（与公司同行业的公司提供更广泛的产品和服务，与公司相比，提供更广泛的产品和服务，更成熟，并在更多样化的市场中运营）。市场法的指导交易方法被考虑过，但由于缺乏有关最近收购与该公司业务类似的公司的可用数据，因此未使用。

        考虑了资产为基础的方法，但没有使用，因为它不能准确反映公司的持续经营价值。

1.3. 收入法

        为了执行此分析，我将构建详细的收入和支出预测。收入预测包括按来源划分的五年收入预测，包括融资、文件和其他服务费。

        费用预测包括与收入相关的人事成本和运营费用的五年预测。五年后，我预计收入和支出预计将以下降的速度增长，达到长期可持续的水平。

        最后，我将根据年度长期增长率、公司贴现率和代表性年份的预计现金流来计算残值。预测的现金流代表了少数股东和控股股东都能够实现的经济学，因此被假定为代表控制和少数价值的前提。

        为简单起见，我将做出以下假设：

• 截至估值日期，以色列的增值税（VAT）税率为17%，预计在整个预测年度内将保持在该水平。
• 截至估值日，以色列的公司税率为23%，预计在整个预测年份内将保持该水平。
• 截至估值日，本公司的折现率为20%。
• 截至估值日，以色列公司的终端增长率为1.5%。
• 根据Aswath Damodaran的数据库，公司的历史5年收入复合年增长率（即复合年增长率）等于行业平均复合年增长率。
• 截至估值日，公司的现金（即公司资产负债表中报告的现金和有价证券）为1.148亿新谢克尔。
• 截至估值日，公司的金融债务（即短期和长期金融债务，但不包括应付账款或非有息负债，如公司资产负债表所示）为3.958亿新谢克尔。

date = {‘December 31, 2020’}
year = [‘2020A’,’%’]
years = [‘2020A’,’2021E’,’2022E’,’2023E’,’2024E’,’2025E’,’Repr. year’]
DiscountPeriod = [0.00, 0.50, 1.50, 2.50, 3.50, 4.50, 5.50]
VAT = 0.17
TAX = 0.23
WACC = 0.20
Perpetuity = 0.015
FinancialDebt = 3958
Cash= 1148

2. 数据理解

        在此阶段，我将采用公司最新的财务报表分析，并从中提取其当前费用和投资率占总收入的百分比。

a = {'Revenue' : [3676,0.00], 'Cost of Goods' : [-1052, 0.00],\'Gross Profit' : [2624,0.00], 'R&D expenses' : [-634,0.00],\'S&M expenses' : [-689,0.00], 'G&A expenses' : [-459,0.00],\'EBIT' : [842,0.00], 'Tax expenses' : [-194,0.00], 'EBIT(1-t)' : [648,0.00],\'Depreciation & Amortization' : [257,0.00], 'EBITDA' : [1099,0.00],\'Capital Expenditures' : [-240,0.00], 'Accounts Receivable' : [577,0.00],\'Inventory' : [38,0.00], 'Accounts Payable' : [198,0.00]}
year = ['2020A','%']
dcf = pd.DataFrame(data=a, index=year)
dcf.T
dcf['Revenue']['%'] = 1.00
dcf['Cost of Goods']['%'] = dcf['Cost of Goods'][years[0]] / dcf['Revenue'][years[0]]
dcf['Gross Profit']['%'] = dcf['Gross Profit'][years[0]] / dcf['Revenue'][years[0]]
dcf['R&D expenses']['%'] = dcf['R&D expenses'][years[0]] / dcf['Revenue'][years[0]]
dcf['S&M expenses']['%'] = dcf['S&M expenses'][years[0]] / dcf['Revenue'][years[0]]
dcf['G&A expenses']['%'] = dcf['G&A expenses'][years[0]] / dcf['Revenue'][years[0]]
dcf['EBIT']['%'] = dcf['EBIT'][years[0]] / dcf['Revenue'][years[0]]
dcf['Tax expenses']['%'] = dcf['Tax expenses'][years[0]] / dcf['EBIT'][years[0]]
dcf['EBIT(1-t)']['%'] = dcf['EBIT(1-t)'][years[0]] / dcf['Revenue'][years[0]]
dcf['Depreciation & Amortization']['%'] = dcf['Depreciation & Amortization'][years[0]] / dcf['Revenue'][years[0]]
dcf['EBITDA']['%'] = dcf['EBITDA'][years[0]] / dcf['Revenue'][years[0]]
dcf['Capital Expenditures']['%'] = dcf['Capital Expenditures'][years[0]] / dcf['Revenue'][years[0]]
dcf['Accounts Receivable']['%'] = dcf['Accounts Receivable'][years[0]] / ( dcf['Revenue'][years[0]]*(1+VAT)/(365*12/12) )
dcf['Inventory']['%'] = -dcf['Inventory'][years[0]] / ( dcf['Cost of Goods'][years[0]]/(365*12/12) )
dcf['Accounts Payable']['%'] = -dcf['Accounts Payable'][years[0]] / ( dcf['Cost of Goods'][years[0]]*(1+VAT)/(365*12/12) )
dcf.T

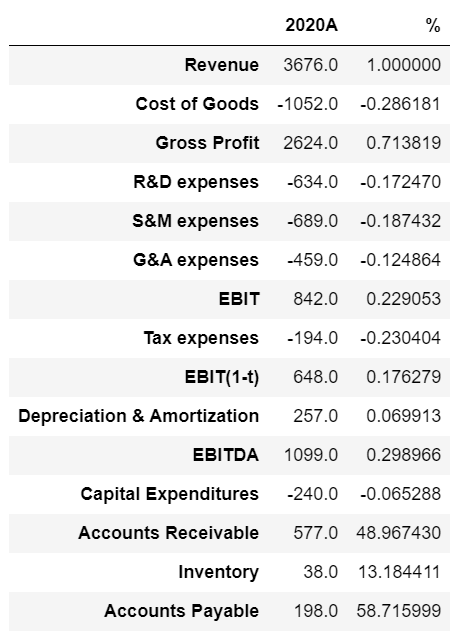
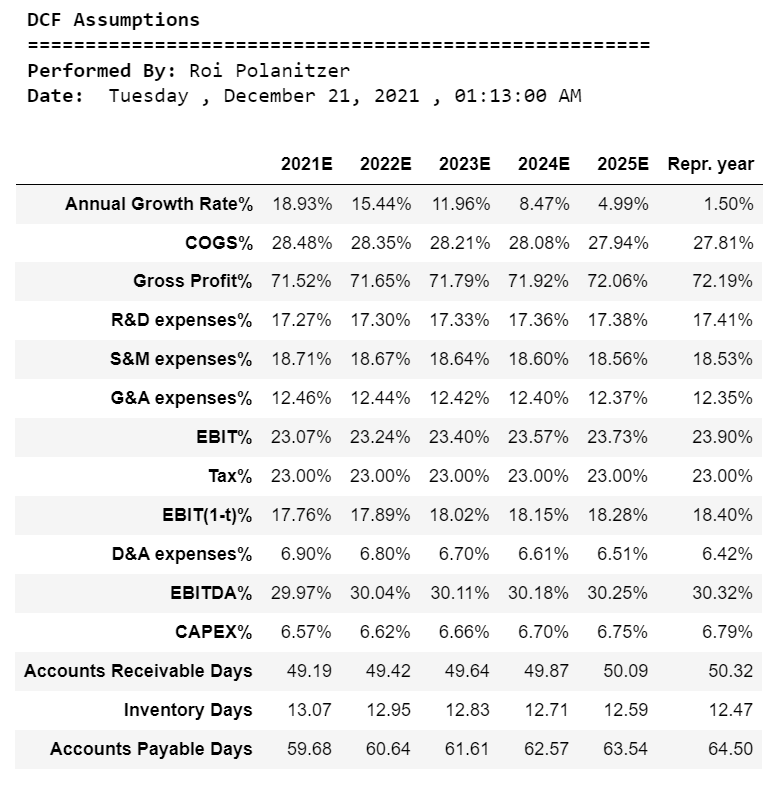
        请注意，“应收账款”、“库存”和“应付账款”余额并未转换为百分比，而是转换为天数（例如应收账款天数、库存天数和应付账款天数）。

3. 数据准备

        在此阶段，我将使用 Aswath Damodaran 的数据库和公司年增长率、费用利润率和投资利润率的均值回归假设来估计将在贴现现金流分析中使用的参数。

        假设回落到平均值，公司当前的每个费用和投资部分将在整个贴现范围内收敛到Damodaran数据库中所述的行业平均水平，而公司5年复合年增长率（即复合年增长率）的收入将在整个贴现范围内收敛到以色列公司的终端增长率（即 1.5%)

from compdata import comp_data
print(comp_data.industry_name_list)

        由于公司属于软件（系统和应用程序）行业，我将采用该行业的参数。

3.1. 复合年增长率

software = comp_data.Industry(‘Software (System & Application)’)
betas = software.get_betas()
sf11 = pd.DataFrame(data = betas)
sf11

print(sf[‘software (system & application)’][2])

18.93%

CAGR = 0.1893

        因此，软件（系统和应用程序）行业平均5年收入复合年增长率估计为18.93%，为了简单起见，我假设公司历史5年收入复合年增长率等于18.93%。

        我假设在未来6年（从2021年到2026年），公司的年增长率预计将遵循平均回归，并从18.93%线性下降到1.5%。

3.2. 销货成本 （COGS） 利润率和毛利率

margins = software.get_margins()
sf1 = pd.DataFrame(data = margins)
sf1

print(sf1[‘software (system & application)’][1])

72.19%

销货成本 = 0.7219–1
销货
成本-0.2781

        因此，软件（系统和应用程序）行业的平均商品销售成本利润率估计为27.81%（我添加一个减号，因为我希望以负值表示商品销售成本）。

        此外，软件（系统与应用）行业平均毛利率估计为72.91%。

3.3. 研发（R&D）费用利润率

print(sf1[‘software (system & application)’][-4])

17.41%

RD = -0.1741

        因此，软件（系统和应用程序）行业的平均研发费用利润率估计为17.41%（我添加一个减号，因为我希望以负数表示研发费用）。

3.4. 销售和营销 （S&M） 费用利润率

print(sf1['software (system & application)'][-3])

30.88%

 SM = -0.6*0.3088
SM 

-0.18528

        根据我作为业务评估师的影响力经验，我假设软件（系统和应用程序）行业平均SG&A费用利润率的60%归因于S&M费用利润率。因此，我估计软件（系统和应用程序）行业的平均S&M费用利润率为18.53%（我添加一个减号，因为我希望以负值表示S&M费用）。

3.5. 一般和行政（G&A）费用利润率

print(sf1['software (system & application)'][-3])

30.88%

GA = -0.4*0.3088
GA 

-0.12352000000000002

        根据我作为业务评估师的经验，我假设软件（系统和应用程序）行业平均SG&A费用利润率的40%归因于G&A费用利润率。因此，我估计软件（系统和应用程序）行业的平均G&A费用利润率为12.35%（我添加一个减号，因为我希望以负数表示G&A费用）。

3.6. 折旧和摊销 （D&A） 费用利润率

capital_expenditures = software.get_capital_expenditures()
sf2 = pd.DataFrame(data = capital_expenditures)
sf2 

我希望将折旧提取到销售利润率，因此我将分两步完成。

第一步：我将从上表中提取销售/资本比率和折旧。

print(sf2[‘software (system & application)’][-1]) 

0.92

print(sf2['software (system & application)'][2]) 

$22，708.04

eva = software.get_eva()
sf3 = pd.DataFrame(data = eva)
sf3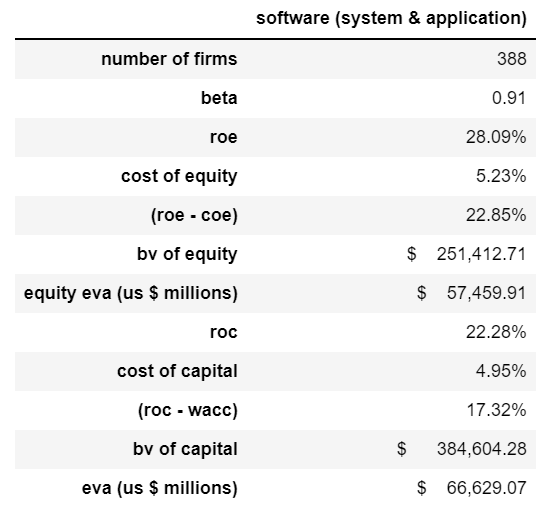 

第二步：我将从第二个表中提取资本的bv。

print(sf3[‘software (system & application)’][-2]) 

$ 384，604.28

现在，首先我将提取销售

Sales = 384604.28 * 0.92
Sales 

353835.93760000006

        然后我将估算D&A费用利润率，如下所示：

DA = 22708.04 / Sales
DA 

0.06417674856325842

        因此，软件（系统和应用程序）行业的平均D&A费用利润率估计为6.42%。

3.7. 资本支出 （CapEx） 保证金

        同样，我希望将资本支出提取到销售利润率中，因此我将分两步完成。

第一步：我将从第一个表中提取资本支出。

print(sf2['software (system & application)'][1]) 

$24，029.65

第二步：我将提取我已经计算过的销售额。

Sales

353835.93760000006

        然后我将估算资本支出利润率，如下所示：

CAPEX = -24029.65 / Sales
CAPEX 

-0.06791184118546131

        因此，软件（系统和应用程序）行业的平均资本支出利润率估计为-6.79%（我添加一个减号，因为我希望以负值表示资本支出）。

3.8. 应收账款天数

sf4 = pd.DataFrame(data = working_capital)
sf4 

print(sf4['software (system & application)'][1]) 

16.13%

        因此，应收账款天数为

ARD = (365*12/12)*0.1613/(1+VAT)
ARD 

50.32008547008547

        因此，软件（系统和应用程序）行业平均应收账款天数估计为50.32天。

3.9. 库存天数

print(sf4['software (system & application)'][2]) 

0.95%

        因此，库存天数为

ID = (365*12/12)*0.0095/(-COGS)
ID 

12.46853649766271

        因此，软件（系统和应用程序）行业的平均库存天数估计为12.46天。

3.10. 应付账款天数

print(sf4['software (system & application)'][3]) 

5.75%

        因此，应付账款天数为

APD = (365*12/12)*(0.0575/(-COGS))/(1+VAT)
APD 

64.50210064018047

        因此，软件（系统和应用程序）行业平均应付账款天数估计为64.50天。

b = {‘Annual Growth Rate%’ : [0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00], ‘COGS%’ : [0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00],\‘Gross Profit%’ : [0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00], ‘R&D expenses%’ : [0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00],\‘S&M expenses%’ : [0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00], ‘G&A expenses%’ : [0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00],\‘EBIT%’ : [0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00], ‘Tax%’ : [0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00],\‘EBIT(1-t)%’ : [0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00], ‘D&A expenses%’ : [0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00],\‘EBITDA%’ : [0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00], ‘CAPEX%’ : [0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00],\‘Accounts Receivable Days’ : [0, 0, 0, 0, 0, 0, 0], ‘Inventory Days’ : [0, 0, 0, 0, 0, 0, 0],\‘Accounts Payable Days’ : [0, 0, 0, 0, 0, 0, 0] }
assumptions = pd.DataFrame(data=b, index=years)
assumptions[‘Annual Growth Rate%’][years[0]] = 1.00
cagr=np.linspace(CAGR,Perpetuity,6)
for i in range(0, len(cagr)):assumptions[‘Annual Growth Rate%’][i+1] = cagr[i]
assumptions[‘COGS%’][years[0]] = dcf[‘Cost of Goods Sold’][‘%’]
cogs=np.linspace(dcf[‘Cost of Goods Sold’][‘%’],COGS,7)
for i in range(1, len(cogs)):assumptions[‘COGS%’][i] = cogs[i]
assumptions[‘Gross Profit%’][years[0]] = dcf[‘Gross Profit’][‘%’]
GP = COGS+1
gp=np.linspace(dcf[‘Gross Profit’][‘%’],GP,7)
for i in range(1, len(gp)):assumptions[‘Gross Profit%’][i] = gp[i]assumptions[‘R&D expenses%’][years[0]] = dcf[‘R&D expenses’][‘%’]
rd=np.linspace(dcf[‘R&D expenses’][‘%’],RD,7)
for i in range(1, len(rd)):assumptions[‘R&D expenses%’][i] = rd[i]assumptions[‘S&M expenses%’][years[0]] = dcf[‘S&M expenses’][‘%’]
sm=np.linspace(dcf[‘S&M expenses’][‘%’],SM,7)
for i in range(1, len(sm)):assumptions[‘S&M expenses%’][i] = sm[i]assumptions[‘G&A expenses%’][years[0]] = dcf[‘G&A expenses’][‘%’]
ga=np.linspace(dcf[‘G&A expenses’][‘%’],GA,7)
for i in range(1, len(ga)):assumptions[‘G&A expenses%’][i] = ga[i]
assumptions[‘Tax%’][years[0]] = dcf[‘Tax expenses’][‘%’]
TA = -TAX
ta=np.linspace(TA,TA,7)
for i in range(1, len(ta)):assumptions[‘Tax%’][i] = ta[i]assumptions[‘D&A expenses%’][years[0]] = dcf[‘Depreciation & Amortization’][‘%’]
da=np.linspace(dcf[‘Depreciation & Amortization’][‘%’],DA,7)
for i in range(1, len(da)):assumptions[‘D&A expenses%’][i] = da[i]
assumptions[‘CAPEX%’][years[0]] = dcf[‘Capital Expenditures’][‘%’]
capex=np.linspace(dcf[‘Capital Expenditures’][‘%’],CAPEX,7)
for i in range(1, len(capex)):assumptions[‘CAPEX%’][i] = capex[i]
assumptions[‘Accounts Receivable Days’] = 0.00
assumptions[‘Accounts Receivable Days’][years[0]] = dcf[‘Accounts Receivable’][‘%’]
ard=np.linspace(dcf[‘Accounts Receivable’][‘%’],ARD,7)
for i in range(1, len(ard)):assumptions[‘Accounts Receivable Days’][i] = ard[i]assumptions[‘Inventory Days’] = 0.00
assumptions[‘Inventory Days’][years[0]] = dcf[‘Inventory’][‘%’]
ind=np.linspace(dcf[‘Inventory’][‘%’],ID,7)
for i in range(1, len(ind)):assumptions[‘Inventory Days’][i] = ind[i]
assumptions[‘Accounts Payable Days’] = 0.00
assumptions[‘Accounts Payable Days’][years[0]] = dcf[‘Accounts Payable’][‘%’]
apd=np.linspace(dcf[‘Accounts Payable’][‘%’],APD,7)
for i in range(1, len(apd)):assumptions[‘Accounts Payable Days’][i] = apd[i]
assumptions.T

请注意，“息税前利润”、“息税前利润（1-t）”和“息税折旧摊销前利润”余额用零填充。这是因为这些余额是计算的结果，我还没有达到计算阶段。

4. 建模

在这个阶段，我将做一些建模。

c = {‘Revenue’ : [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], ‘Cost of Goods Sold’ : [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],\‘Gross Profit’ : [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], ‘R&D expenses’ : [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],\‘S&M expenses’ : [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], ‘G&A expenses’ : [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],\‘EBIT’ : [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], ‘Tax expenses’ : [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],\‘EBIT(1-t)’ : [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], ‘Depreciation & Amortization’ : [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],\‘EBITDA’ : [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], ‘Capital Expenditures’ : [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],\‘Accounts Receivable’ : [0, 0, 0, 0, 0, 0, 0], ‘Inventory’ : [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],\‘Accounts Payable’ : [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], ‘Non-Cash WC’ : [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],\‘Change in WC’ : [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], ‘Free Cash Flow’ : [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],\‘Discounting Horizon’ : DiscountPeriod }
dcf1 = pd.DataFrame(data=c, index=years)
dcf1[‘Revenue’][years[0]] = dcf[‘Revenue’][years[0]]
for i in range(1, len(dcf1[‘Revenue’])):dcf1[‘Revenue’][i] = dcf1[‘Revenue’][i-1]*(1 + assumptions[‘Annual Growth Rate%’][i] )dcf1[‘Cost of Goods Sold’][years[0]] = dcf[‘Cost of Goods Sold’][years[0]]
for i in range(1, len(dcf1[‘Revenue’])):dcf1[‘Cost of Goods Sold’][i] = dcf1[‘Revenue’][i] * assumptions[‘COGS%’][i]dcf1[‘Gross Profit’][years[0]] = dcf[‘Gross Profit’][years[0]]
for i in range(1, len(dcf1[‘Revenue’])):dcf1[‘Gross Profit’][i] = dcf1[‘Revenue’][i] + dcf1[‘Cost of Goods Sold’][i]dcf1[‘R&D expenses’][years[0]] = dcf[‘R&D expenses’][years[0]]
for i in range(1, len(dcf1[‘Revenue’])):dcf1[‘R&D expenses’][i] = dcf1[‘Revenue’][i] * assumptions[‘R&D expenses%’][i]dcf1[‘S&M expenses’][years[0]] = dcf[‘S&M expenses’][years[0]]
for i in range(1, len(dcf1[‘Revenue’])):dcf1[‘S&M expenses’][i] = dcf1[‘Revenue’][i] * assumptions[‘S&M expenses%’][i]dcf1[‘G&A expenses’][years[0]] = dcf[‘G&A expenses’][years[0]]
for i in range(1, len(dcf1[‘Revenue’])):dcf1[‘G&A expenses’][i] = dcf1[‘Revenue’][i] * assumptions[‘G&A expenses%’][i]dcf1[‘EBIT’][years[0]] = dcf[‘EBIT’][years[0]]
for i in range(1, len(dcf1[‘Revenue’])):dcf1[‘EBIT’][i] = dcf1[‘Gross Profit’][i] + dcf1[‘R&D expenses’][i] + dcf1[‘S&M expenses’][i] + dcf1[‘G&A expenses’][i]for i in range(1, len(ga)):assumptions[‘EBIT%’][i] = dcf1[‘EBIT’][i]/dcf1[‘Revenue’][i]dcf1[‘Tax expenses’][years[0]] = dcf[‘Tax expenses’][years[0]]
for i in range(1, len(dcf1[‘Revenue’])):dcf1[‘Tax expenses’][i] = dcf1[‘EBIT’][i] * assumptions[‘Tax%’][i]assumptions[‘EBIT(1-t)%’][years[0]] = dcf[‘EBIT(1-t)’][‘%’]
dcf1[‘EBIT(1-t)’][years[0]] = dcf[‘EBIT(1-t)’][years[0]]
for i in range(1, len(dcf1[‘Revenue’])):dcf1[‘EBIT(1-t)’][i] = dcf1[‘EBIT’][i] + dcf1[‘Tax expenses’][i] for i in range(1, len(ga)):assumptions[‘EBIT(1-t)%’][i] = dcf1[‘EBIT(1-t)’][i] / dcf1[‘Revenue’][i]dcf1[‘Depreciation & Amortization’][years[0]] = dcf[‘Depreciation & Amortization’][years[0]]
for i in range(1, len(dcf1[‘Revenue’])):dcf1[‘Depreciation & Amortization’][i] = dcf1[‘Revenue’][i] * assumptions[‘D&A expenses%’][i]assumptions[‘EBITDA%’][years[0]] = dcf[‘EBITDA’][‘%’]
dcf1[‘EBITDA’][years[0]] = dcf[‘EBITDA’][years[0]]
for i in range(1, len(dcf1[‘Revenue’])):dcf1[‘EBITDA’][i] = dcf1[‘EBIT’][i] + dcf1[‘Depreciation & Amortization’][i] for i in range(1, len(ga)):assumptions[‘EBITDA%’][i] = dcf1[‘EBITDA’][i] / dcf1[‘Revenue’][i]dcf1[‘Capital Expenditures’][years[0]] = dcf[‘Capital Expenditures’][years[0]]
for i in range(1, len(dcf1[‘Revenue’])):dcf1[‘Capital Expenditures’][i] = dcf1[‘Revenue’][i] * assumptions[‘CAPEX%’][i]dcf1[‘Accounts Receivable’] = 0.00
dcf1[‘Accounts Receivable’][years[0]] = dcf[‘Accounts Receivable’][years[0]]
for i in range(1, len(dcf1[‘Revenue’])):dcf1[‘Accounts Receivable’][i] = dcf1[‘Revenue’][i] * assumptions[‘Accounts Receivable Days’][i] * (1+VAT) / (365*12/12)dcf1[‘Inventory’] = 0.00
dcf1[‘Inventory’][years[0]] = dcf[‘Inventory’][years[0]]
for i in range(1, len(dcf1[‘Revenue’])):dcf1[‘Inventory’][i] = -dcf1[‘Cost of Goods Sold’][i] * assumptions[‘Inventory Days’][i] / (365*12/12)dcf1[‘Accounts Payable’] = 0.00
dcf1[‘Accounts Payable’][years[0]] = dcf[‘Accounts Payable’][years[0]]
for i in range(1, len(dcf1[‘Revenue’])):dcf1[‘Accounts Payable’][i] = -dcf1[‘Cost of Goods Sold’][i] * assumptions[‘Accounts Payable Days’][i] * (1+VAT) / (365*12/12)for i in range(0, len(dcf1[‘Revenue’])):dcf1[‘Non-Cash WC’][i] = dcf1[‘Accounts Receivable’][i] + dcf1[‘Inventory’][i] — dcf1[‘Accounts Payable’][i]for i in range(1, len(dcf1[‘Revenue’])):dcf1[‘Change in WC’][i] = -( dcf1[‘Non-Cash WC’][i] — dcf1[‘Non-Cash WC’][i-1] )for i in range(1, len(dcf1[‘Revenue’])):dcf1[‘Free Cash Flow’][i] = dcf1[‘EBIT(1-t)’][i] + dcf1[‘Depreciation & Amortization’][i] + dcf1[‘Capital Expenditures’][i] + dcf1[‘Change in WC’][i] dcf1[‘Present Value of Free Cash Flow’]=0.00
for i in range(1, (len(dcf1[‘Revenue’])) ):dcf1[‘Present Value of Free Cash Flow’][i] = dcf1[‘Free Cash Flow’][i] / (1 + WACC) ** dcf1[‘Discounting Horizon’][i]dcf1[‘Future Value of Terminal Value’]= 0.00
dcf1[‘Future Value of Terminal Value’][years[6]] = dcf1[‘Free Cash Flow’][years[6]]*(1+Perpetuity)/(WACC-Perpetuity)
dcf1.T.style.format(“{:,.1f}”)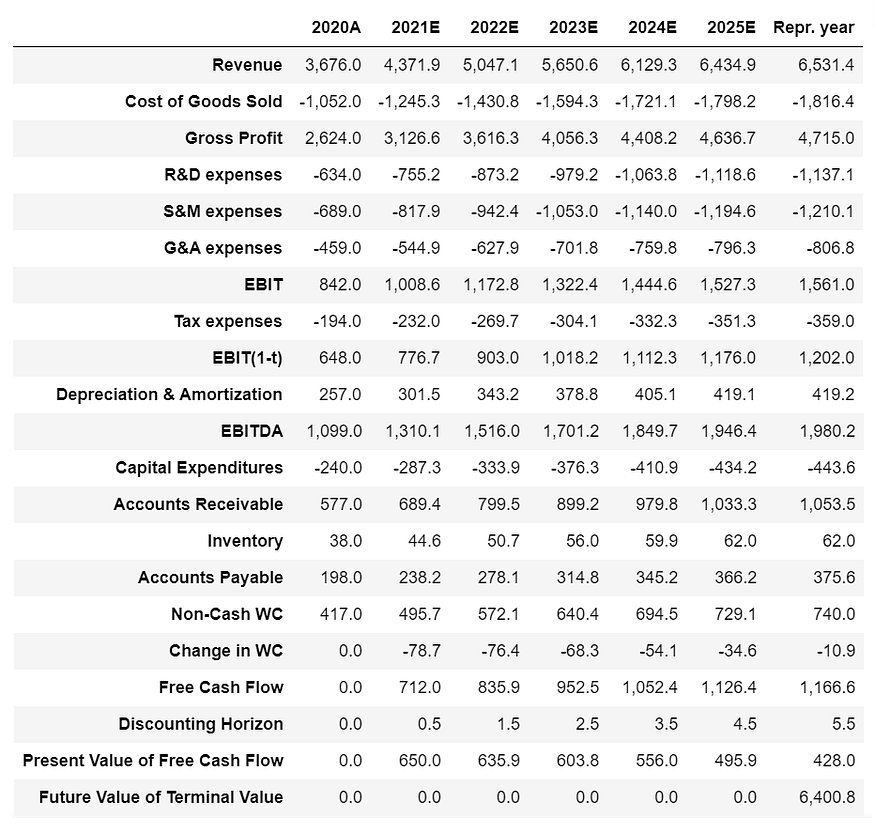

收入
        收入预计将从2020年的约36.760亿新谢克尔增至2025年的约64.349亿新谢克尔，五年复合年增长率为11.85%。

FiveYearCAGR = (dcf1[‘Revenue’][years[5]] / dcf1[‘Revenue’][years[0]])**(1/5)-1
FiveYearCAGR

0.11849330982812556

4.1 终端价值

        终端值表示贴现现金流模型中与收益相关的现金流期末的企业价值，此时预期收益将趋于稳定。终值基于终值现金流倍数 5.49。

TerminalValueToCashFlowMultiple = dcf1[‘Future Value of Terminal Value’][years[6]] / dcf1[‘Free Cash Flow’][years[6]]
TerminalValueToCashFlowMultiple

5.486486486486486

        该倍数是使用戈登增长模型计算的 - 在预测期的最后一年将现金流资本化为资本化率[基于WACC（20%）减去预期的长期增长（1.5%）]。

        1.5%的终端增长率是根据公司的长期增长预期和市场对未来通胀的预期确定的。资本化率应用于增长调整后的终年现金流，以确定终值。

5. 评估

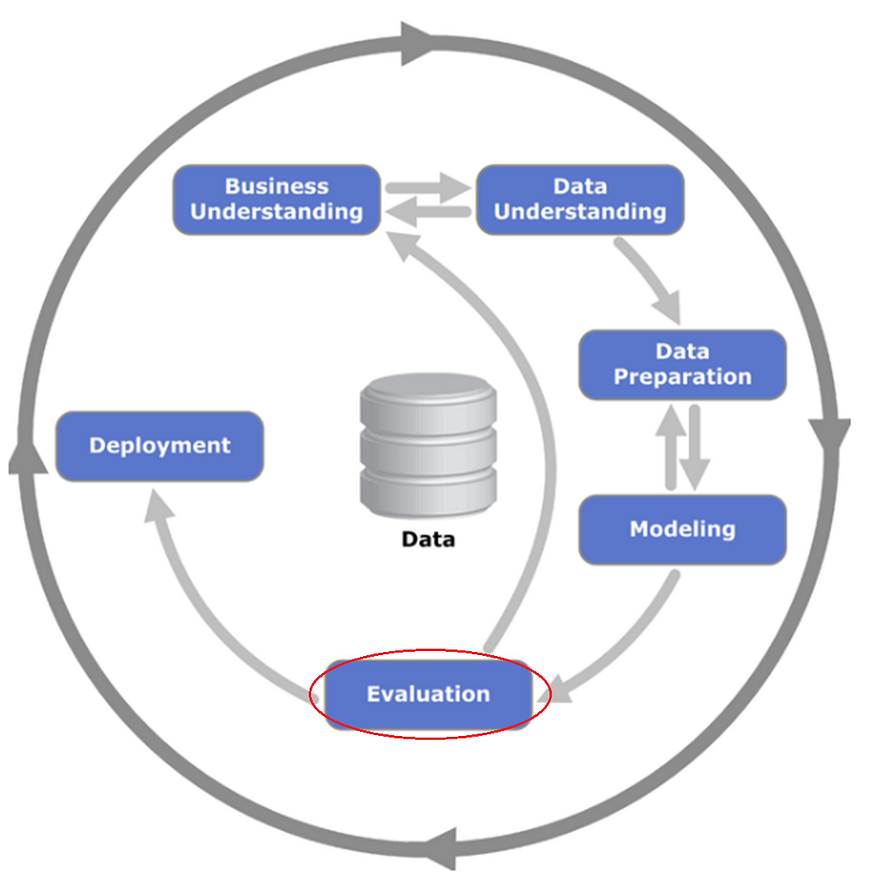
在这个阶段，我将最终评估公司的股权。

d2 = {‘Sum of Discounted Free Cash Flows’ : [0.00], ‘Discounted Terminal Value’ : [0.00],\‘Enterprise Value’: [0.00], ‘Financial Debt’ : [0.00], ‘Cash’ : [0.00],\‘Net Financial Debt’ : [0.00], ‘Equity value’: [0.00]}
dcf2 = pd.DataFrame(data=d2,index=date)
dcf2[‘Sum of Discounted Free Cash Flows’] = np.sum(dcf1[‘Present Value of Free Cash Flow’])
dcf2[‘Discounted Terminal Value’] = ( dcf1[‘Future Value of Terminal Value’][years[6]] ) / (1+WACC)**dcf1[‘Discounting Horizon’][years[6]]
dcf2[‘Enterprise Value’] = dcf2[‘Sum of Discounted Free Cash Flows’] + dcf2[‘Discounted Terminal Value’]
dcf2[‘Financial Debt’] = FinancialDebt
dcf2[‘Cash’] = Cash
dcf2[‘Net Financial Debt’] = dcf2[‘Financial Debt’] — dcf2[‘Cash’]
dcf2[‘Equity value’] = dcf2[‘Enterprise Value’] — dcf2[‘Net Financial Debt’]
dcf2.T.style.format(“{:,.1f}”)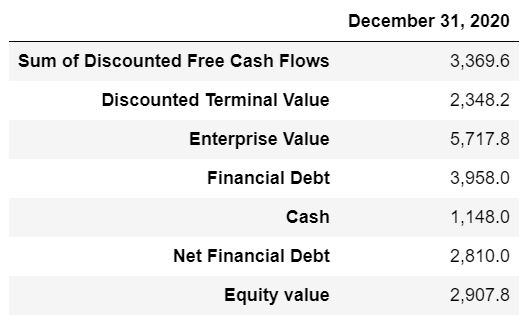

        使用上述贴现率计算预测期和终期的现金流量并贴现至估值日。根据上述数据和方法，截至估值日，公司的股权价值为2.907亿新谢克尔。

6. 部署

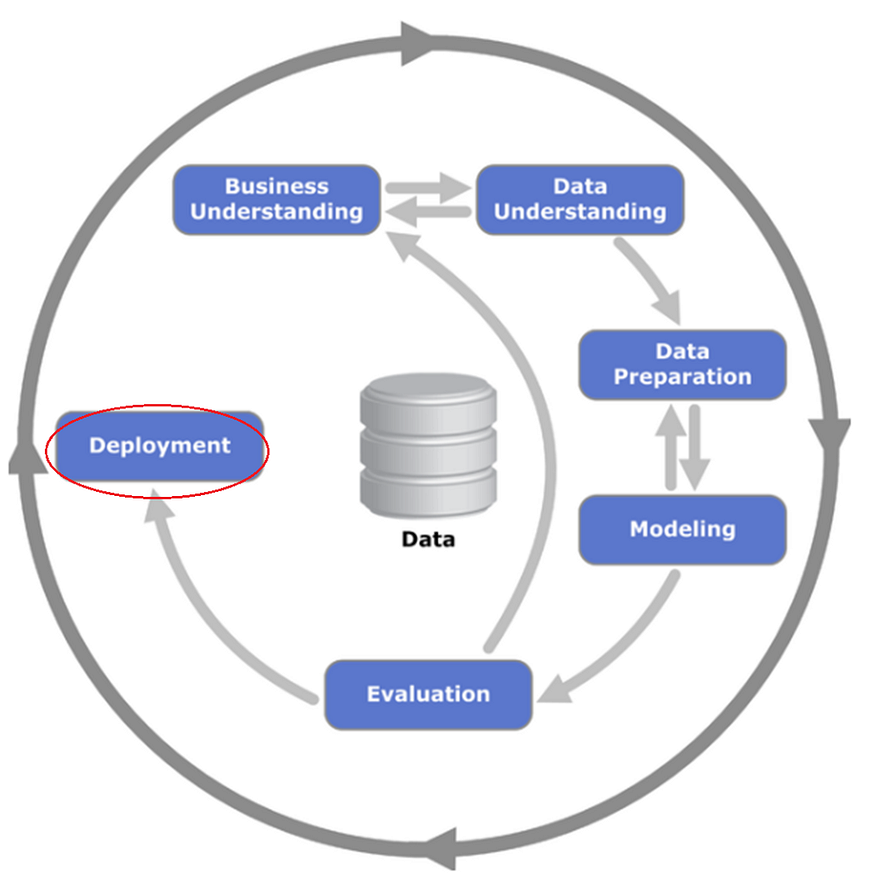
        评估员的部署阶段是编写评估报告的阶段，该报告解释了评估中使用的方法和开发的模型。

assumptions1 = assumptions.copy()
assumptions1[‘COGS%’] = -assumptions1[‘COGS%’]
assumptions1[‘R&D expenses%’] = -assumptions1[‘R&D expenses%’]
assumptions1[‘S&M expenses%’] = -assumptions1[‘S&M expenses%’]
assumptions1[‘G&A expenses%’] = -assumptions1[‘G&A expenses%’]
assumptions1[‘Tax%’] = -assumptions1[‘Tax%’]
assumptions1[‘CAPEX%’] = -assumptions1[‘CAPEX%’]
assumptions1[‘Annual Growth Rate%’] = assumptions1[‘Annual Growth Rate%’].apply(‘{:.2%}’.format)
assumptions1[‘COGS%’] = assumptions1[‘COGS%’].apply(‘{:.2%}’.format)
assumptions1[‘Gross Profit%’] = assumptions1[‘Gross Profit%’].apply(‘{:.2%}’.format)
assumptions1[‘R&D expenses%’] = assumptions1[‘R&D expenses%’].apply(‘{:.2%}’.format)
assumptions1[‘S&M expenses%’] = assumptions1[‘S&M expenses%’].apply(‘{:.2%}’.format)
assumptions1[‘G&A expenses%’] = assumptions1[‘G&A expenses%’].apply(‘{:.2%}’.format)
assumptions1[‘EBIT%’] = assumptions1[‘EBIT%’].apply(‘{:.2%}’.format)
assumptions1[‘Tax%’] = assumptions1[‘Tax%’].apply(‘{:.2%}’.format)
assumptions1[‘EBIT(1-t)%’] = assumptions1[‘EBIT(1-t)%’].apply(‘{:.2%}’.format)
assumptions1[‘D&A expenses%’] = assumptions1[‘D&A expenses%’].apply(‘{:.2%}’.format)
assumptions1[‘EBITDA%’] = assumptions1[‘EBITDA%’].apply(‘{:.2%}’.format)
assumptions1[‘CAPEX%’] = assumptions1[‘CAPEX%’].apply(‘{:.2%}’.format)
assumptions2 = assumptions1.copy()
assumptions2[‘Accounts Receivable Days’] = assumptions2[‘Accounts Receivable Days’].apply(‘{:,.2f}’.format)
assumptions2[‘Inventory Days’] = assumptions2[‘Inventory Days’].apply(‘{:,.2f}’.format)
assumptions2[‘Accounts Payable Days’] = assumptions2[‘Accounts Payable Days’].apply(‘{:,.2f}’.format)
assumptions3 = assumptions2.T
assumptions3.drop([years[0]],axis=1, inplace=True)
from datetime import date
today = date.today()
now = datetime.now()
import calendar
curr_date = date.today()
print(“\033[1m DCF Assumptions”)
print(“\033[0m ======================================================”)
print(“\033[1m Performed By:”,”\033[0mRoi Polanitzer”)
print(“\033[1m Date:”,”\033[0m”,calendar.day_name[curr_date.weekday()],”,”,today.strftime(“%B %d, %Y”),”,”,now.strftime(“%H:%M:%S AM”))
assumptions3
>

financial = dcf1.copy()
financial.drop([‘Discounting Horizon’,’Present Value of Free Cash Flow’,’Future Value of Terminal Value’,\‘Depreciation & Amortization’, ‘Capital Expenditures’,’Accounts Receivable’,’Inventory’,\‘Accounts Payable’,’Non-Cash WC’,’Change in WC’,’Free Cash Flow’], axis=1, inplace=True)
financial = financial.T.style.format(“{:,.1f}”)
print(“\033[1m Financial Projection”)
print(“\033[0m ======================================================”)
print(“\033[1m Performed By:”,”\033[0mRoi Polanitzer”)
print(“\033[1m Date:”,”\033[0m”,calendar.day_name[curr_date.weekday()],”,”,today.strftime(“%B %d, %Y”),”,”,now.strftime(“%H:%M:%S AM”))
financial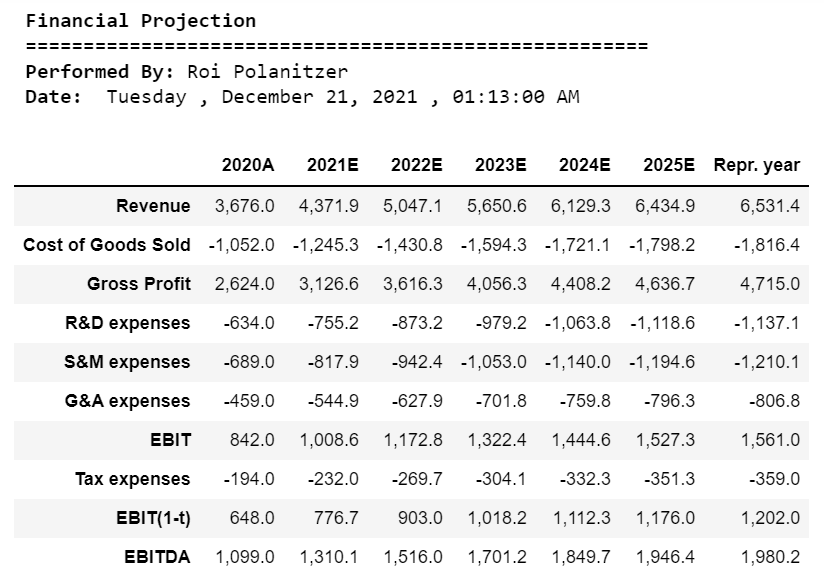

investment = dcf1[ [‘Depreciation & Amortization’, ‘Capital Expenditures’,’Accounts Receivable’,\‘Inventory’,’Accounts Payable’,’Non-Cash WC’,’Change in WC’] ]
investment1 = investment.copy()
investment1.drop([years[0]], axis=0, inplace=True)
investment1 = investment1.T.style.format(“{:,.1f}”)
print(“\033[1m Investments Forecast”)
print(“\033[0m ======================================================”)
print(“\033[1m Performed By:”,”\033[0mRoi Polanitzer”)
print(“\033[1m Date:”,”\033[0m”,calendar.day_name[curr_date.weekday()],”,”,today.strftime(“%B %d, %Y”),”,”,now.strftime(“%H:%M:%S AM”))
investment1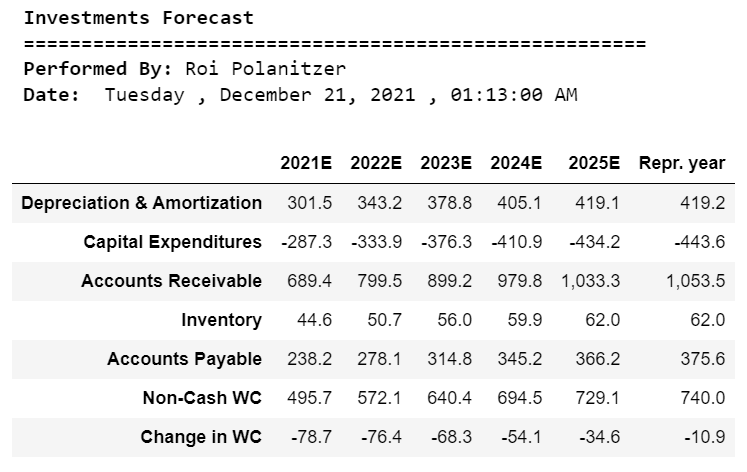

forecast = dcf1[ [‘Free Cash Flow’, ‘Discounting Horizon’,’Present Value of Free Cash Flow’,’Future Value of Terminal Value’] ]
forecast1 = forecast.copy()
forecast1.drop([years[0]], axis=0, inplace=True)
forecast1 = forecast1.T.style.format(“{:,.1f}”)
print(“\033[1m Discounted Cash Flow Analysis”)
print(“\033[0m ======================================================”)
print(“\033[1m Performed By:”,”\033[0mRoi Polanitzer”)
print(“\033[1m Date:”,”\033[0m”,calendar.day_name[curr_date.weekday()],”,”,today.strftime(“%B %d, %Y”),”,”,now.strftime(“%H:%M:%S AM”))
forecast1

summary = dcf3.copy()
summary = summary.T.style.format(“{:,.1f}”)
print(“\033[1m DCF Summary”)
print(“\033[0m ======================================================”)
print(“\033[1m Performed By:”,”\033[0mRoi Polanitzer”)
print(“\033[1m Date:”,”\033[0m”,calendar.day_name[curr_date.weekday()],”,”,today.strftime(“%B %d, %Y”),”,”,now.strftime(“%H:%M:%S AM”))
summary

6.1 灵敏度分析

        下表列出了公司权益公允价值对资本成本变化和长期增长率变化的敏感性分析（所有金额均以百万新谢克尔表示）：

c1 = { ‘ ‘ : [ ‘Sensitivity Analysis’,(Perpetuity-0.01),(Perpetuity-0.005), Perpetuity, (Perpetuity+0.005), (Perpetuity+0.01)], ‘WACC — 1%’ : [ (WACC-0.01), 0.00, 0.00, 0.00, 0.00, 0.00], ‘WACC — 0.5%’ : [ (WACC-0.005), 0.00, 0.00, 0.00, 0.00, 0.00],\‘WACC’ : [ (WACC), 0.00, 0.00, 0.00, 0.00, 0.00], ‘WACC + 0.5%’ : [ (WACC+0.005), 0.00, 0.00, 0.00, 0.00, 0.00],\‘WACC + 1%’ : [ (WACC+0.01), 0.00, 0.00, 0.00, 0.00, 0.00] }
c2 = [‘’,’Perpetuity + 1%’, ‘Perpetuity + 0.5%’, ‘Perpetuity’, ‘Perpetuity — 0.5%’, ‘Perpetuity — 1%’]
sensitivity = pd.DataFrame(data=c1, index=c2)
fcf1 = dcf1[‘Free Cash Flow’][years[1]]
fcf2 = dcf1[‘Free Cash Flow’][years[2]]
fcf3 = dcf1[‘Free Cash Flow’][years[3]]
fcf4 = dcf1[‘Free Cash Flow’][years[4]]
fcf5 = dcf1[‘Free Cash Flow’][years[5]]
fcf6 = dcf1[‘Free Cash Flow’][years[6]]
tcf1 = dcf1[‘Discounting Horizon’][years[1]]
tcf2 = dcf1[‘Discounting Horizon’][years[2]]
tcf3 = dcf1[‘Discounting Horizon’][years[3]]
tcf4 = dcf1[‘Discounting Horizon’][years[4]]
tcf5 = dcf1[‘Discounting Horizon’][years[5]]
tcf6 = dcf1[‘Discounting Horizon’][years[6]]
D = dcf2[‘Net Financial Debt’][0]
for x in range(1, len(sensitivity[‘WACC — 1%’])):for y in range(1, len(sensitivity[‘WACC — 1%’])):wacc = sensitivity.iloc[0,y]g = sensitivity.iloc[x,0]cap = wacc-gsensitivity.iloc[x,y] = fcf1/(1+wacc)**tcf1 + fcf2/(1+wacc)**tcf2 + fcf3/(1+wacc)**tcf3 + fcf4/(1+wacc)**tcf4 +\fcf5/(1+wacc)**tcf5 + fcf6/(1+wacc)**tcf6 + (fcf6*(1+g)/cap)/(1+wacc)**tcf6 — dcf2[‘Net Financial Debt’]
sensitivity1 = sensitivity.copy()
for x in range(1, len(sensitivity[‘WACC — 1%’])):for y in range(1, len(sensitivity[‘WACC — 1%’])):sensitivity1.iloc[x,y] = “{:,.1f}”.format(float(sensitivity.iloc[x,y]))sensitivity1.iloc[0,1] = “{:.2%}”.format(sensitivity.iloc[0,1]) 
sensitivity1.iloc[0,2] = “{:.2%}”.format(sensitivity.iloc[0,2]) 
sensitivity1.iloc[0,3] = “{:.2%}”.format(sensitivity.iloc[0,3]) 
sensitivity1.iloc[0,4] = “{:.2%}”.format(sensitivity.iloc[0,4]) 
sensitivity1.iloc[0,5] = “{:.2%}”.format(sensitivity.iloc[0,5]) 
sensitivity1.iloc[1,0] = “{:.2%}”.format(sensitivity.iloc[1,0]) 
sensitivity1.iloc[2,0] = “{:.2%}”.format(sensitivity.iloc[2,0]) 
sensitivity1.iloc[3,0] = “{:.2%}”.format(sensitivity.iloc[3,0]) 
sensitivity1.iloc[4,0] = “{:.2%}”.format(sensitivity.iloc[4,0]) 
sensitivity1.iloc[5,0] = “{:.2%}”.format(sensitivity.iloc[5,0])
print(“\033[1m Sensitivity Analysis”)
print(“\033[0m ======================================================”)
print(“\033[1m Performed By:”,”\033[0mRoi Polanitzer”)
print(“\033[1m Date:”,”\033[0m”,calendar.day_name[curr_date.weekday()],”,”,today.strftime(“%B %d, %Y”),”,”,now.strftime(“%H:%M:%S AM”))
sensitivity1.T

6.2 置信区间

        通常，评估师被要求给出一系列值而不是单一值，因此他必须为公司的股权价值构建 95% 的置信区间。

from scipy.stats import norm
from numpy.random import randn
from numpy import random as rn
import scipy.stats as si
def normsinv(x):x = si.norm.ppf(x)return (x)
Z = normsinv(0.9500)
Z

1.959963984540054

        对应于 95% 置信区间的标准正态偏差为 Z_MIN ≈ −1.96 和 Z_MAX ≈ 1.96。换句话说，每条尾部都有 2.5%。

        公司股权价值的 95% 置信区间为

MIN_value = Mean_value − 1.96×StandardError

and

MAX_value = Mean_value + 1.96×标准误差

        其中Mean_value为2.907亿新谢克尔。

Mean_value = dcf2[‘Equity value’][0]
Mean_value 

2907.7749213080497

        让我们从敏感度分析数据框中获取所有净值并估计标准误差

value = []
for x in range(1, len(sensitivity[‘WACC — 1%’])):for y in range(1, len(sensitivity[‘WACC — 1%’])):value.append(float(sensitivity.iloc[x,y]))StandardError = np.std(value)/np.sqrt(len(value))
StandardError 

49.35817218013521

MIN_value = Mean_value - Z*StandardError
MIN_value 

2811.0346814922577

MAX_value = Mean_value + Z*StandardError
MAX_value 

3004.5151611238416

        因此，95% 置信区间范围为 2.811 亿新谢克尔到 0.3 亿新谢克尔。

        我们可以解释这个置信区间，即我们95%确信截至估值日公司的股权价值在2.811亿新谢克尔至0.3亿新谢克尔之间。也就是说，每个方向与从 DCF 模型获得的值的偏差为 004.5%。

        我认为，根据上述和以下保留意见，截至估值日，公司的股权价值估计在2，811.0-3.004亿新谢克尔（预期价值为5.2亿新谢克尔）的范围内。