2、matlab判断广义积分的敛散性（含完整代码）

在 MATLAB 中，可以使用 integral 函数来计算广义积分，并通过计算积分的结果来判断其敛散性。

具体来说，如果广义积分 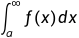或 收敛，则其对应的定积分 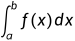在 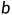趋近于无穷时也收敛；反之，若定积分 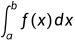在 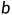趋近于无穷时发散，则广义积分 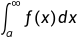或 也发散。

因此，可以先计算定积分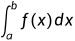，再逐步增大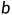，计算对应的积分值，直到积分值趋于稳定或趋近于无穷大。如果积分值趋近于一个有限的值，则广义积分收敛；如果积分值趋近于无穷大或发散，则广义积分发散。

以下是一个示例代码，用于判断广义积分 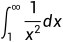是否收敛：

f = @(x) 1./x.^2;  % 定义函数
a = 1;  % 积分下限
b = a + 1;  % 积分上限，从1开始增加
tol = 1e-6;  % 允许的误差
integral_val = integral(f, a, b, 'RelTol', tol);  % 计算定积分的值
while abs(integral_val) < 1e6  % 如果积分值趋近于无穷大，则停止迭代b = b + 1;  % 增加积分上限last_val = integral_val;  % 保存上一个积分值integral_val = integral(f, a, b, 'RelTol', tol);  % 计算新的积分值if abs(integral_val - last_val) < tol  % 如果积分值趋近于稳定，则停止迭代break;end
end
if abs(integral_val) < 1e6  % 如果积分值趋近于一个有限的值，则广义积分收敛disp('The improper integral converges.');
else  % 否则广义积分发散disp('The improper integral diverges.');
end

输出结果为：

The improper integral converges.

因为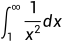 收敛，所以输出结果为“广义积分收敛”。