461.汉明距离·Brian Kernighan 算法

链接：https://leetcode.cn/problems/hamming-distance/solution/chun-c-by-xun-ge-v-bzf6/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。 

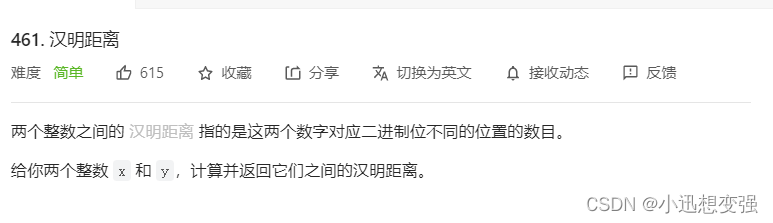
题目

示例

思路

解题思路
两个数字对应二进制位不同的位置的数目。只需将两个数按位异或就可以得到不同位数的二进制数
异或 -> 相同为0，不同为1,按位异或，可以对两个数中相同的位置0，不同的位置1
然后统计一下异或之后的数有多少位为1即可
统计二进制数为1的位数和

1. 按位移动

• 我们可以不断地检查 s 的最低位，如果最低位为 1，那么令计数器加一，然后我们令 s 整体右移一位，这样 s 的最低位将被舍去，原本的次低位就变成了新的最低位。我们重复这个过程直到 s=0 为止。这样计数器中就累计了 s 的二进制表示中 1 的数量

1. Brian Kernighan 算法

• 我们可以使用 Brian Kernighan 算法进行优化，具体地，该算法可以被描述为这样一个结论：记 f(x) 表示 x 和 x−1 进行与运算所得的结果（即 f(x)= x & (x−1)），那么 f(x) 恰为 x 删去其二进制表示中最右侧的 1 的结果。基于该算法，当我们计算 s=x⊕y，只需要不断让 s=f(s)，直到 s=0 即可。这样每循环一次，s 都会删去其二进制表示中最右侧的 1，最终循环的次数即为 s 的二进制表示中 1 的数量。

代码

按位移动

/*
*int hammingDistance：计算两个整数之间的汉明距离
int x：整数x
int y：整数y
返回值：汉明距离
*/
int hammingDistance(int x, int y){int s = x ^ y; int ret = 0;while(s){if(s & 1){ret++;}s >> 1;}return ret;
}

Brian Kernighan 算法

/*
*int hammingDistance：计算两个整数之间的汉明距离
int x：整数x
int y：整数y
返回值：汉明距离
*/
int hammingDistance(int x, int y){int s = x ^ y; int ret = 0;while(s){s &= s-1;ret++;}return ret;
}

时间空间复杂度