本文主要是介绍同步电机自感计算推导,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
参考文献
Sychronous Machines Theory and Performances Charles Concordia
数学推导
以下图所示进行自感推导,推导原理:双反应理论,a相磁动势在dq轴的分量,dq轴磁动势产生的磁通再在a轴交链产生a相的磁链。
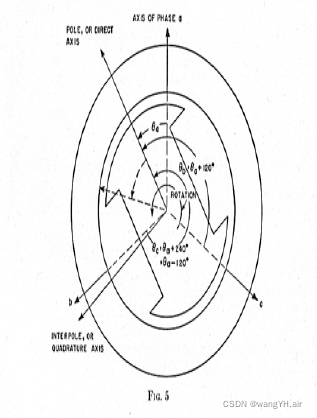
自感计算方法
计算定子间自感: a 相在 d 轴产生的磁动势: m m f a d = N i a cos θ a a 相在 q 轴产生的磁动势: m m f a q = − N i a sin θ a d 轴磁动势在 a 相产生的磁链: ψ a a d = N ∗ k ∗ m m f a d ℜ max cos θ a d 轴对应最大气隙,对应最大磁阻 ℜ max ψ a a q = − N ∗ k ∗ m m f a q ℜ min sin θ a q 轴对应最小气隙,对应最小磁阻 ℜ min \text{计算定子间自感:} \\ a\text{相在}d\text{轴产生的磁动势:} \\ mmf_{ad}=Ni_a\cos \theta _a \\ a\text{相在}q\text{轴产生的磁动势:} \\ mmf_{aq}=-Ni_a\sin \theta _a \\ d\text{轴磁动势在}a\text{相产生的磁链:} \\ \psi _{aad}=N*k*\frac{mmf_{ad}}{\Re _{\max}}\cos \theta _a \\ d\text{轴对应最大气隙,对应最大磁阻}\Re _{\max} \\ \psi _{aaq}=-N*k*\frac{mmf_{aq}}{\Re _{\min}}\sin \theta _a \\ q\text{轴对应最小气隙,对应最小磁阻}\Re _{\min} 计算定子间自感:a相在d轴产生的磁动势:mmfad=Niacosθaa相在q轴产生的磁动势:mmfaq=−Niasinθad轴磁动势在a相产生的磁链:ψaad=N∗k∗ℜmaxmmfadcosθad轴对应最大气隙,对应最大磁阻ℜmaxψaaq=−N∗k∗ℜminmmfaqsinθaq轴对应最小气隙,对应最小磁阻ℜmin
2. 计算总自感
ψ a a d = k N 2 ℜ max i a cos 2 θ a ψ a a q = k N 2 ℜ min i a sin 2 θ a L a a = ( ψ a b d + ψ a b q ) / i a L a a = k N 2 ℜ max cos 2 θ a + k N 2 ℜ min sin 2 θ a L a a = P d cos 2 θ a + P q sin 2 θ a L a a = P d cos 2 θ a + P d sin 2 θ a − P d sin 2 θ a + P q sin 2 θ a L a a = P d − ( P d − P q ) sin 2 θ a \psi _{aad}=\frac{kN^2}{\Re _{\max}}i_a\cos ^2\theta _a \\ \psi _{aaq}=\frac{kN^2}{\Re _{\min}}i_a\sin ^2\theta _a \\ L_{aa}=\left( \psi _{abd}+\psi _{abq} \right) /i_a \\ L_{aa}=\frac{kN^2}{\Re _{\max}}\cos ^2\theta _a+\frac{kN^2}{\Re _{\min}}\sin ^2\theta _a \\ L_{aa}=P_d\cos ^2\theta _a+P_q\sin ^2\theta _a \\ L_{aa}=P_d\cos ^2\theta _a+P_d\sin ^2\theta _a-P_d\sin ^2\theta _a+P_q\sin ^2\theta _a \\ L_{aa}=P_d-\left( P_d-P_q \right) \sin ^2\theta _a ψaad=ℜmaxkN2iacos2θaψaaq=ℜminkN2iasin2θaLaa=(ψabd+ψabq)/iaLaa=ℜmaxkN2cos2θa+ℜminkN2sin2θaLaa=Pdcos2θa+Pqsin2θaLaa=Pdcos2θa+Pdsin2θa−Pdsin2θa+Pqsin2θaLaa=Pd−(Pd−Pq)sin2θa
积化和差公式
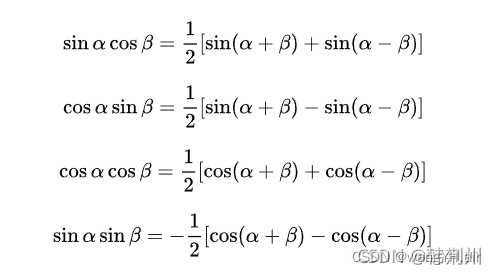
3. 自感计算简化:
L a a = P d + ( P d − P q ) 1 2 [ cos 2 θ a − 1 ] L a a = ( P d + P q ) 2 + ( P d − P q ) 2 cos ( 2 θ a ) 令: P d + P q 2 = L A , P d − P q 2 = L B L a a = L A + L B cos ( 2 θ a ) L_{aa}=P_d+\left( P_d-P_q \right) \frac{1}{2}\left[ \cos 2\theta _a-1 \right] \\ L_{aa}=\frac{\left( P_d+P_q \right)}{2}+\frac{\left( P_d-P_q \right)}{2}\cos \left( 2\theta _a \right) \\ \text{令:}\frac{P_d+P_q}{2}=L_A, \frac{P_d-P_q}{2}=L_B \\ L_{aa}=L_A+L_B\cos \left( 2\theta _a \right) Laa=Pd+(Pd−Pq)21[cos2θa−1]Laa=2(Pd+Pq)+2(Pd−Pq)cos(2θa)令:2Pd+Pq=LA,2Pd−Pq=LBLaa=LA+LBcos(2θa)
这篇关于同步电机自感计算推导的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






