本文主要是介绍辐射度量学、光度学、BRDF,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
最近可能要用到光照渲染和3D人脸模型,补了很多基础知识(球谐光照、Phong模型、3DMM等)。但是对最基本的光的概念还是模糊不清,曾尝试学习被劝退多次,这里写篇博客彻底总结下!
目录
- 辐射度量学
- 基本概念
- Radiant Energy 辐射能
- Lumious Energy 光量
- Radiant Flux(power) 辐射通量(功率)
- Luminous Flux 光通量
- Luminosity Function光度(视见)函数
- Solid Angle 立体角
- Radiant Intensity 辐射强度
- Luminous Intensity 发光强度
- Irradiance 辐照度
- Illuminance 光照度
- Radiance 辐射亮度
- Luminance 光亮度
- Bidirectional Reflectance Distribution Function 双向反射分布函数
- The Reflection Equation 反射方程
- The Rendering Equation 渲染方程
- 递归情况与Ray Tracing光线追踪
- Path Tracing 路径追踪
辐射度量学
基本概念
- 辐射度量学 Radiometry:研究电磁辐射能测量的科学,是辐射能本身的客观度量
- 光度学 photometry:使人眼产生目视刺激的度量,包括光辐射能的客观度量和人眼视觉的生理因素两者相互对应的物理量,是主观度量
- 许多百科和教程对各个物理量的中文翻译十分混乱,这里贴一个正确的!

下文以辐射度量学为主,光度学顺带介绍
Radiant Energy 辐射能
一个区域中光子能量的总和
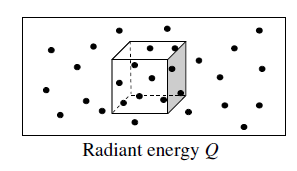
Q [ J = J o u l e ] Q\ [J=Joule] Q [J=Joule]
- 图形学中少用。光能并不会停留和储存在某个位置,而是在始终不断运动着的
- 照的时间越长,能量越多,所以常常分析单位时间
Lumious Energy 光量
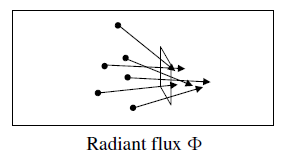
Radiant Flux(power) 辐射通量(功率)
单位时间穿过截面的光能:
Φ = d Q d t [ W = W a t t ] \Phi = \frac{dQ}{dt}\ [W=Watt] Φ=dtdQ [W=Watt]
Luminous Flux 光通量
人眼感受到的功率,单位是Lm=lumen.
- 可以认为luminous flux是主观物理量,反映视觉明亮程度;而radiant flux是客观物理量,反映光辐射强度;下文其他辐射度物理量和光度物理量也有类似关系
Luminosity Function光度(视见)函数
- 将radiant energy转换为luminous energy。也可用于其他辐射物理量和光物理量之间的转换,道理是相同的
- 不同波长的光luminosity function不同。具体数值参考Wiki. 人眼对黄绿光最敏感,红紫光则不敏感
Solid Angle 立体角
前置知识,后文会用
在球坐标系下,
d Ω = d A r 2 = ( r d θ ) ( r sin θ d φ ) r 2 = sin θ d θ d φ d\Omega=\frac{dA}{r^2}=\frac{(rd\theta)(r\sin\theta d\varphi)}{r^2}=\sin\theta d\theta d\varphi dΩ=r2dA=r2(rdθ)(rsinθdφ)=sinθdθdφ

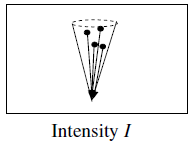
Radiant Intensity 辐射强度
给定方向上单位立体角内的辐射功率
I = d Φ d Ω [ W / s r = W / s t e r a d i a n ] I=\frac{d\Phi}{d\Omega}\ [W/sr=W/steradian] I=dΩdΦ [W/sr=W/steradian]
Luminous Intensity 发光强度
单位lm/sr=cd=candela
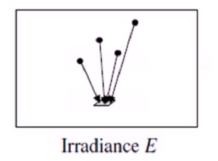
Irradiance 辐照度
反映物体表面受光能的影响程度,单位面积上的光通量:
E = d Φ d A [ W / m 2 ] E=\frac{d\Phi}{dA}\ [W/m^2] E=dAdΦ [W/m2]
Illuminance 光照度
每单位面积所接收到的光通量,单位是 l m / m 2 = l u x lm/m^2=lux lm/m2=lux勒克斯
Radiance 辐射亮度
物体表面沿某一方向的明亮程度,它等于单位投影面积和单位立体角上的光通量
L = ∂ 2 Φ c o s θ ∂ A ∂ Ω [ W / ( m 2 s r ) ] L=\frac{\partial^2\Phi}{cos\theta \partial A \partial \Omega}\ [W/(m^2 sr)] L=cosθ∂A∂Ω∂2Φ [W/(m2sr)]
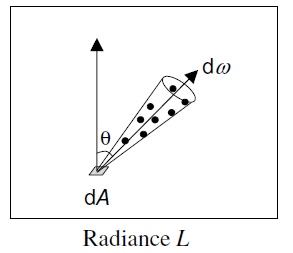
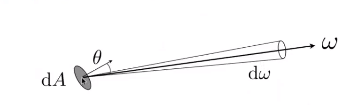
- Radiance: Irradiance per solid angle
d E ( x , ω ) = L i ( x , ω ) cos θ d ω E ( x ) = ∫ H 2 L i ( x , ω ) cos θ d ω \begin{aligned} dE(x,\omega) &=L_i (x,\omega)\cos \theta d\omega \\ E(x) &= \int_{H^2} L_i(x, \omega)\cos \theta d\omega \end{aligned} dE(x,ω)E(x)=Li(x,ω)cosθdω=∫H2Li(x,ω)cosθdω
这里 H 2 H^2 H2是半球面 - Radiance: Intensity per projected unit area
Luminance 光亮度
单位 c d / m 2 = l m / ( s r m 2 ) = n i t cd/m^2=lm/(sr\ m^2)=nit cd/m2=lm/(sr m2)=nit
Bidirectional Reflectance Distribution Function 双向反射分布函数
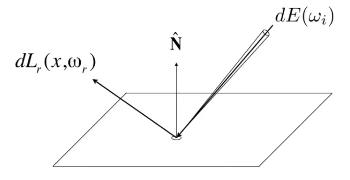
从 ω i \omega_i ωi,以 d ω i d\omega_i dωi为立体角入射的照度 d E dE dE,被面积 d A dA dA接收,向 ω o \omega_o ωo射出的亮度
d E ( ω i ) = L ( ω i ) cos θ i d ω i dE(\omega_i)=L(\omega_i)\cos\theta_id\omega_i \\ dE(ωi)=L(ωi)cosθidωi
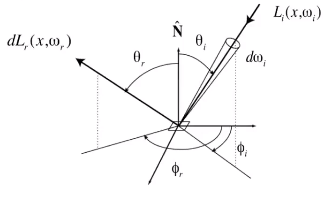
BRDF表示从 ω i \omega_i ωi入射的光有多少到 ω r \omega_r ωr出射
f r ( ω i → ω r ) = d L r ( ω r ) d E i ( ω i ) = d L r ( ω r ) L i ( ω i ) cos θ i d ω i [ 1 s r ] f_r(\omega_i \rightarrow \omega_r)=\frac{dL_r(\omega_r)}{dE_i(\omega_i)}=\frac{dL_r(\omega_r)}{L_i(\omega_i)\cos\theta_i d\omega_i} \quad \left[\frac{1}{sr}\right] fr(ωi→ωr)=dEi(ωi)dLr(ωr)=Li(ωi)cosθidωidLr(ωr)[sr1]
这里 d L r ( ω r ) dL_r(\omega_r) dLr(ωr)是仅受 d E i ( ω i ) dE_i(\omega_i) dEi(ωi)影响产生
- BRDF定义了不同的材质
The Reflection Equation 反射方程

L r ( x , ω r ) = ∫ H 2 f r ( x , ω i → ω r ) L i ( x , ω i ) cos θ i d ω i L_r(x,\omega_r)=\int_{H^2} f_r(x, \omega_i \rightarrow \omega_r)L_i(x, \omega_i)\cos \theta_i d\omega_i Lr(x,ωr)=∫H2fr(x,ωi→ωr)Li(x,ωi)cosθidωi
注意入射光 L i L_i Li可能来自其他反射,而并非光源。这样就需要Recursive Equation递归方程
The Rendering Equation 渲染方程

反射方程基础上增加自身发射项
L o ( x , ω o ) = L e ( x , ω o ) + ∫ H 2 f r ( x , ω i , ω o ) L i ( x , ω i ) ( n ⋅ ω i ) d ω i L_o(x,\omega_o)=L_e(x, \omega_o) + \int_{H^2} f_r(x, \omega_i, \omega_o)L_i(x, \omega_i) (n\cdot \omega_i) d\omega_i Lo(x,ωo)=Le(x,ωo)+∫H2fr(x,ωi,ωo)Li(x,ωi)(n⋅ωi)dωi
这里我们记 ω i \omega_i ωi向外(虽然光确实向内,我们只是这么记)
递归情况与Ray Tracing光线追踪

在考虑多次光线碰撞的渲染中,该式改写为
L r ( x , ω r ) = L e ( x , ω r ) + ∫ Ω f ( x , ω i , ω r ) L r ( x ′ , − ω i ) cos θ i d ω i L_r(x,\omega_r)=L_e(x, \omega_r) + \int_{\Omega} f(x, \omega_i, \omega_r)L_r(x', -\omega_i) \cos\theta_i d\omega_i Lr(x,ωr)=Le(x,ωr)+∫Ωf(x,ωi,ωr)Lr(x′,−ωi)cosθidωi
注意这里没有 L i , L o L_i, L_o Li,Lo,全部都是反射 L r L_r Lr,(有点类似马尔科夫随机过程稳态的感觉)
在实际渲染中 f , θ , ω , L e f, \theta, \omega, L_e f,θ,ω,Le都是已知的,而 L r L_r Lr则是未知的,也就是我们要算的东西
该方程符合第二类Fredholm integral equation,这里略去一大波推导,可以简写为
l ( u ) = e ( u ) + ∫ l ( v ) K ( u , v ) d v l(u)=e(u)+\int l(v) K(u,v)dv l(u)=e(u)+∫l(v)K(u,v)dv
这里 l l l相当于radiance, u , v u,v u,v相当于两个位置,这里方向全都忽略掉了. 其中 K ( u , v ) d v K(u,v)dv K(u,v)dv是Light Transport Operator.
这是一个Linear Operator Equation,可进一步简写为
L = E + K L L=E+KL L=E+KL
该公式可离散化为线性方程组
- L , E L,E L,E是向量,表示不同位置的光, L L L是全局光照. K K K是Light Transport Matrix光传输矩阵
- 可采用一般数值蒙特卡洛方法求解
- 同时估计所有光路
L = ( I − K ) − 1 E = ( I + K + K 2 + ⋯ ) E \begin{aligned} L&=(I-K)^{-1}E \\ &=(I+K+K^2+\cdots)E \end{aligned} L=(I−K)−1E=(I+K+K2+⋯)E
这里的分解有实际物理意义!

Path Tracing 路径追踪
在计算连续积分时,通过蒙特卡洛积分进行离散化,对于渲染方程中积分项
∫ H 2 f r ( x , ω i , ω o ) L i ( x , ω i ) ( n ⋅ ω i ) d ω i ≈ 1 N ∑ i = 1 N L i ( x , ω i ) f r ( x , ω i , ω o ) ( n ⋅ ω i ) p ( ω i ) \begin{aligned} & \int_{H^2} f_r(x, \omega_i, \omega_o)L_i(x, \omega_i) (n\cdot \omega_i) d\omega_i \\ \approx &\frac{1}{N}\sum_{i=1}^N \frac{L_i(x,\omega_i)f_r(x, \omega_i, \omega_o)(n\cdot \omega_i)}{p(\omega_i)} \end{aligned} ≈∫H2fr(x,ωi,ωo)Li(x,ωi)(n⋅ωi)dωiN1i=1∑Np(ωi)Li(x,ωi)fr(x,ωi,ωo)(n⋅ωi)
也即选了 N N N个方向进行计算,这里我们可以计算 P P P点从各个入射方向来的光照


当考虑多次弹射时,光线数量将达到 N # b o u n c e s N^{\#bounces} N#bounces次,但是当 N = 1 N=1 N=1时,就不会计算爆炸. 这就叫路径追踪. 这里结果很Noisy,但是如果用多个Path,就会好很多

这里递归终止条件如果采用固定次数上限,则会产生能量损失。一种期望下没有损失的方法是Russian Roulette俄罗斯轮盘赌,类似Dropout,详见GAMES101

为了更准确探测到光源,这里采样可以不用半球上的均匀采样,改用从光源采样,细节略。
还可以把上述两个方法结合起来,认为亮度来自两个部分:
- 光源(直接,光源采样)
- 其他反射(间接,引入俄罗斯轮盘赌)
参考资料:
[1] GAMES101-现代计算机图形学入门-闫令琪
[2] 计算机图形学-高林
[3] Wikipedia
[4] https://www.zhihu.com/question/58979753/answer/257412924
这篇关于辐射度量学、光度学、BRDF的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




![【课程笔记】谭平计算机视觉(Computer Vision)[4]:辐射校准高动态范围图像 - Radiometric Calibration HDR](https://i-blog.csdnimg.cn/blog_migrate/7972a564ea1c037d7366163813d67ddb.png)


