【数据结构C/C++】顺序与链式二叉树创建与前中后、层序遍历

2023-10-11 06:01
文章标签 二叉树 遍历 c++ 数据结构 创建 层序 顺序 链式 中后

本文主要是介绍【数据结构C/C++】顺序与链式二叉树创建与前中后、层序遍历，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

  • 顺序存储结构二叉树
  • 链式存储结构二叉树
  • 刷题推荐
  • 408考研各数据结构C/C++代码（Continually updating）

顺序存储结构二叉树

顺序存储结构的二叉树的特点在于，其使用数组存放二叉树中的每一个节点。
我们设定根节点的数组索引下标为n（n>=1），那么有当前根节点的左子树节点在数组中的下标为2n，右子树在数组中的下标为2n+1。
上面是顺序存储结构二叉树的最最最重要的一个特性，我们后面的所有操作都基于这个理论。
相对于比较简单的对于链式存储结构的二叉树的遍历，以及计算最大二叉树深度，链式存储结构都会更加接单，而顺序存储结构则需要考虑到当前节点是否为空，并且当前索引是否超出了树当前最大的节点个数。

LeetCode计算二叉树最大深度
在这里插入图片描述

这里我不推荐你花大把时间去实现一个顺序存储结构的二叉树的层序遍历，因为我们知道，层序遍历一般的解法都是配合一个队列或者栈来实现的。
我在写Java的时候一般都会使用Deque也就是双端队列来实现，但是C语言并没有提供这样子的功能，你还得手动实现，比较费时，因此我不太推荐。
当然，有兴趣的可以去刷一下LeetCode链式存储结构的层序遍历，还是比较常见的。

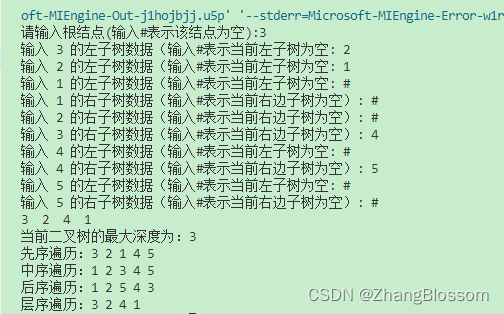
先附上一张代码运行的图片。
在这里插入图片描述

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <math.h>#define MaxSize 100typedef char TreeNodeType;//二叉树结构
typedef struct
{TreeNodeType data[MaxSize];int BiTreeNum;
} BinaryTree;// 声明队列数据结构
typedef struct
{int front, rear;int size;int capacity;int *array;
} Queue;void initTree(BinaryTree *T);
void createTree(BinaryTree *T, int n);
TreeNodeType rootTree(BinaryTree *T);
int countTree(BinaryTree *T);
int maxDepthOfTree(BinaryTree *T, int n);
void preOrderTraverse(BinaryTree *T, int n);
void inOrderTraverse(BinaryTree *T, int n);
void postOrderTraverse(BinaryTree *T, int n);
void levelOrderTraverse(BinaryTree *T); // 层序遍历
bool destoryTree(BinaryTree *T);
void traverseArray(BinaryTree *T); // 遍历数组// 队列相关函数
Queue *createQueue(int capacity);
bool isQueueEmpty(Queue *queue);
bool isQueueFull(Queue *queue);
void enqueue(Queue *queue, int item);
int dequeue(Queue *queue);int main()
{BinaryTree T;// 开始构造二叉树 其中使用1作为根节点下标// 而不是使用0，使用0的问题在于不好表示数据在数组中的位置// 我们知道二叉树满足 当前节点n的左子树和右子树的序列号应该为 2n和2n+1initTree(&T);printf("请输入根结点(输入#表示该结点为空):");createTree(&T, 1);traverseArray(&T);printf("当前二叉树的最大深度为：%d\n", maxDepthOfTree(&T, 1));printf("先序遍历：");preOrderTraverse(&T, 1);printf("\n");printf("中序遍历：");inOrderTraverse(&T, 1);printf("\n");printf("后序遍历：");postOrderTraverse(&T, 1);printf("\n");printf("层序遍历：");levelOrderTraverse(&T);printf("\n");return 0;
}void initTree(BinaryTree *T)
{int i;for (i = 0; i < MaxSize; ++i){T->data[i] = '\0';}T->BiTreeNum = 0;return;
}void createTree(BinaryTree *T, int n)
{char ch;// 刷新（清空）标准输入流（stdin）// 主打一个求稳fflush(stdin);// 输入当前节点信息 # 代表当前节点为空// 先构造过字数scanf(" %c", &ch);if (ch == '#'){ // 空直接返回return;}else{T->data[n] = ch;T->BiTreeNum++;printf("输入 %c 的左子树数据（输入#表示当前左子树为空: ", ch);// 这里有一个技巧createTree(T, 2 * n);printf("输入 %c 的右子树数据（输入#表示当前右边子树为空）: ", ch);createTree(T, (2 * n + 1));}
}// 计算二叉树的最大深度
// 从根节点到叶子节点的最长路径的长度
// 由于是顺序结构 因此这里从第一层也就是n=1开始向下遍历
// 然后不断的判断左子树和右子树的高度
// 最后取最大值
int maxDepthOfTree(BinaryTree *T, int n)
{if (n <= T->BiTreeNum && T->data[n] != '\0'){int leftDepth = maxDepthOfTree(T, 2 * n);int rightDepth = maxDepthOfTree(T, 2 * n + 1);return 1 + fmax(leftDepth, rightDepth);}else{return 0;}
}//先序遍历 根左右
void preOrderTraverse(BinaryTree *T, int n)
{if (T->data[n] == '\0')return;else{printf("%c ", T->data[n]);preOrderTraverse(T, 2 * n);preOrderTraverse(T, (2 * n + 1));}
}
//中序遍历 左根由7
void inOrderTraverse(BinaryTree *T, int n)
{if (T->data[n] == '\0')return;else{inOrderTraverse(T, 2 * n);printf("%c ", T->data[n]);inOrderTraverse(T, (2 * n + 1));}
}
//后序遍历  左右根
void postOrderTraverse(BinaryTree *T, int n)
{if (T->data[n] == '\0')return;else{postOrderTraverse(T, 2 * n);postOrderTraverse(T, (2 * n + 1));printf("%c ", T->data[n]);}
}
void traverseArray(BinaryTree *T){for(int i=1;i<=T->BiTreeNum;i++){printf("%c  ",T->data[i]);}printf("\n");
}// 层序遍历二叉树
void levelOrderTraverse(BinaryTree *T)
{if (T->BiTreeNum == 0){printf("二叉树为空\n");return;}//创建一个队列存放当前层Queue *queue = createQueue(T->BiTreeNum);int current = 1; // 从根节点开始//结束条件while (current <= T->BiTreeNum){printf("%c ", T->data[current]);//判断左子树是否存在 存在就放入队列if (2 * current <= T->BiTreeNum && T->data[2 * current] != '\0'){enqueue(queue, 2 * current);}//判断右子树是否存在 存在就放入队列if (2 * current + 1 <= T->BiTreeNum && T->data[2 * current + 1] != '\0'){enqueue(queue, 2 * current + 1);}//出队对头 if (!isQueueEmpty(queue)){current = dequeue(queue);}else{break;}}//使用完毕释放空间free(queue->array);free(queue);
}// 创建队列
Queue *createQueue(int capacity)
{Queue *queue = (Queue *)malloc(sizeof(Queue));if (!queue){perror("内存分配失败");exit(EXIT_FAILURE);}queue->front = 0;queue->rear = -1;queue->size = 0;queue->capacity = capacity;queue->array = (int *)malloc(capacity * sizeof(int));if (!queue->array){perror("内存分配失败");exit(EXIT_FAILURE);}return queue;
}// 检查队列是否为空
bool isQueueEmpty(Queue *queue)
{return (queue->size == 0);
}// 检查队列是否已满
bool isQueueFull(Queue *queue)
{return (queue->size == queue->capacity);
}// 入队列
void enqueue(Queue *queue, int item)
{if (isQueueFull(queue)){printf("队列已满\n");return;}queue->rear = (queue->rear + 1) % queue->capacity;queue->array[queue->rear] = item;queue->size++;
}// 出队列
int dequeue(Queue *queue)
{if (isQueueEmpty(queue)){printf("队列为空\n");return -1;}int item = queue->array[queue->front];queue->front = (queue->front + 1) % queue->capacity;queue->size--;return item;
}

链式存储结构二叉树

链式存储结构构造一个二叉树就比较简单，并且无论是遍历操作还是追求最大深度，都可以比较容易的求解。
其主要的重点在于结构体的定义，链式存储结构的精髓在于，左右指针域。

// 定义二叉树结点结构
typedef struct TreeNode
{int data;struct TreeNode *left; //左右指针struct TreeNode *right;
} TreeNode;

在这里插入图片描述

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <math.h>#define MaxSize 100
// 定义二叉树结点结构
typedef struct TreeNode
{int data;struct TreeNode *left;struct TreeNode *right;
} TreeNode;// 函数声明
TreeNode *createNode(int data);
TreeNode *insert(TreeNode *root, int data);
TreeNode *search(TreeNode *root, int data);
TreeNode *findMin(TreeNode *root);
TreeNode *deleteNode(TreeNode *root, int data);
void preorderTraversal(TreeNode *root);
void inorderTraversal(TreeNode *root);
void postorderTraversal(TreeNode *root);
int maxDepthOfTree(TreeNode *root);
void levelOrderTraversal(TreeNode *root);TreeNode *root = NULL;int main()
{int choice, data;printf("基于链式存储结构的二叉树操作：\n");while (1){printf("\n请选择操作：\n");printf("1. 插入\n");printf("2. 删除\n");printf("3. 查找\n");printf("4. 层序遍历\n");scanf("%d", &choice);switch (choice){case 1:printf("输入要插入的数据: ");scanf("%d", &data);root = insert(root, data);printf("前序遍历结果为：");preorderTraversal(root);printf("中序遍历结果为：");inorderTraversal(root);printf("后序遍历结果为：");postorderTraversal(root);printf("二叉树最大深度为：%d\n", maxDepthOfTree(root));break;case 2:printf("输入要删除的数据: ");scanf("%d", &data);root = deleteNode(root, data);printf("前序遍历结果为：");preorderTraversal(root);printf("中序遍历结果为：");inorderTraversal(root);printf("后序遍历结果为：");postorderTraversal(root);printf("二叉树最大深度为：%d\n", maxDepthOfTree(root));break;case 3:printf("输入要查找的数据: ");scanf("%d", &data);TreeNode *result = search(root, data);if (result != NULL){printf("找到了 %d\n", result->data);}else{printf("未找到 %d\n", data);}printf("前序遍历结果为：");preorderTraversal(root);printf("中序遍历结果为：");inorderTraversal(root);printf("后序遍历结果为：");postorderTraversal(root);printf("二叉树最大深度为：%d\n", maxDepthOfTree(root));break;case 4:printf("层序遍历结果为：");levelOrderTraversal(root);printf("\n");break;}}return 0;
}// 创建新的二叉树结点
TreeNode *createNode(int data)
{TreeNode *newNode = (TreeNode *)malloc(sizeof(TreeNode));if (newNode == NULL){perror("内存分配失败");exit(EXIT_FAILURE);}newNode->data = data;newNode->left = NULL;newNode->right = NULL;return newNode;
}// 插入结点
TreeNode *insert(TreeNode *root, int data)
{if (root == NULL){return createNode(data);}if (data < root->data){root->left = insert(root->left, data);}else if (data > root->data){root->right = insert(root->right, data);}return root;
}// 查找结点
TreeNode *search(TreeNode *root, int data)
{if (root == NULL || root->data == data){return root;}if (data < root->data){return search(root->left, data);}else{return search(root->right, data);}
}// 找到最小值结点
TreeNode *findMin(TreeNode *root)
{while (root->left != NULL){root = root->left;}return root;
}// 删除结点
TreeNode *deleteNode(TreeNode *root, int data)
{if (root == NULL){return root;}if (data < root->data){root->left = deleteNode(root->left, data);}else if (data > root->data){root->right = deleteNode(root->right, data);}else{// 结点有一个子结点或没有子结点if (root->left == NULL){TreeNode *temp = root->right;free(root);return temp;}else if (root->right == NULL){TreeNode *temp = root->left;free(root);return temp;}// 结点有两个子结点，找到中序遍历的后继结点（右子树中的最小值）TreeNode *temp = findMin(root->right);root->data = temp->data;root->right = deleteNode(root->right, temp->data);}return root;
}// 前序遍历
void preorderTraversal(TreeNode *root)
{if (root != NULL){printf("%d ", root->data);preorderTraversal(root->left);preorderTraversal(root->right);}
}// 中序遍历
void inorderTraversal(TreeNode *root)
{if (root != NULL){inorderTraversal(root->left);printf("%d ", root->data);inorderTraversal(root->right);}
}// 后序遍历
void postorderTraversal(TreeNode *root)
{if (root != NULL){postorderTraversal(root->left);postorderTraversal(root->right);printf("%d ", root->data);}
}// 计算二叉树的最大深度
int maxDepthOfTree(TreeNode *root)
{if (root == NULL){return 0;}else{int leftHeight = maxDepthOfTree(root->left);int rightHeight = maxDepthOfTree(root->right);return fmax(leftHeight, rightHeight) + 1;}
}// 层序遍历
void levelOrderTraversal(TreeNode *root)
{if (root == NULL){return;}// 创建一个队列用于层序遍历TreeNode *queue[MaxSize];int front = 0, rear = 0;queue[rear++] = root; // 根结点入队while (front < rear){TreeNode *current = queue[front++];printf("%d ", current->data);// 左子结点入队if (current->left != NULL){queue[rear++] = current->left;}// 右子结点入队if (current->right != NULL){queue[rear++] = current->right;}}
}

刷题推荐

LeetCode树类型题目
树类型的题目其实是我刷的最多的，因为其实只要找到规律了，做起来就最快，直接往递归这一条路上去考虑即可。
在这里插入图片描述

408考研各数据结构C/C++代码（Continually updating）

408考研各数据结构C/C++代码（Continually updating）
这个模块是我应一些朋友的需求，希望我能开一个专栏，专门提供考研408中各种常用的数据结构的代码，并且希望我附上比较完整的注释以及提供用户输入功能，ok，fine，这个专栏会一直更新，直到我认为没有新的数据结构可以讲解了。
目前我比较熟悉的数据结构如下：
数组、链表、队列、栈、树、B/B+树、红黑树、Hash、图。
所以我会先有空更新出如下几个数据结构的代码，欢迎关注。 当然，在我前两年的博客中，对于链表、哈夫曼树等常用数据结构，我都提供了比较完整的详细的实现以及思路讲解，有兴趣可以去考古。

这篇关于【数据结构C/C++】顺序与链式二叉树创建与前中后、层序遍历的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/186059。

相关文章

C++11范围for初始化列表auto decltype详解

C++11范围for初始化列表auto decltype详解

《C++11范围for初始化列表autodecltype详解》C++11引入auto类型推导、decltype类型推断、统一列表初始化、范围for循环及智能指针,提升代码简洁性、类型安全与资源管理效... 目录C++11新特性1. 自动类型推导auto1.1 基本语法2. decltype3. 列表初始化3
阅读更多...
C++11右值引用与Lambda表达式的使用

C++11右值引用与Lambda表达式的使用

《C++11右值引用与Lambda表达式的使用》C++11引入右值引用,实现移动语义提升性能,支持资源转移与完美转发；同时引入Lambda表达式,简化匿名函数定义,通过捕获列表和参数列表灵活处理变量... 目录C++11新特性右值引用和移动语义左值 / 右值常见的左值和右值移动语义移动构造函数移动复制运算符
阅读更多...
Spring Bean初始化及@PostConstruc执行顺序示例详解

Spring Bean初始化及@PostConstruc执行顺序示例详解

《SpringBean初始化及@PostConstruc执行顺序示例详解》本文给大家介绍SpringBean初始化及@PostConstruc执行顺序,本文通过实例代码给大家介绍的非常详细,对大家的... 目录1. Bean初始化执行顺序2. 成员变量初始化顺序2.1 普通Java类（非Spring环境）(
阅读更多...
C++中detach的作用、使用场景及注意事项

C++中detach的作用、使用场景及注意事项

《C++中detach的作用、使用场景及注意事项》关于C++中的detach,它主要涉及多线程编程中的线程管理,理解detach的作用、使用场景以及注意事项,对于写出高效、安全的多线程程序至关重要,下... 目录一、什么是join()？它的作用是什么？类比一下：二、join()的作用总结三、join()怎么
阅读更多...
C++中全局变量和局部变量的区别

C++中全局变量和局部变量的区别

《C++中全局变量和局部变量的区别》本文主要介绍了C++中全局变量和局部变量的区别,全局变量和局部变量在作用域和生命周期上有显著的区别,下面就来介绍一下,感兴趣的可以了解一下... 目录一、全局变量定义生命周期存储位置代码示例输出二、局部变量定义生命周期存储位置代码示例输出三、全局变量和局部变量的区别作用域
阅读更多...
C++中assign函数的使用

C++中assign函数的使用

《C++中assign函数的使用》在C++标准模板库中,std::list等容器都提供了assign成员函数,它比操作符更灵活,支持多种初始化方式,下面就来介绍一下assign的用法,具有一定的参考价... 目录​1.assign的基本功能​​语法​2. 具体用法示例​​​(1) 填充n个相同值​​(2)
阅读更多...
IntelliJ IDEA2025创建SpringBoot项目的实现步骤

IntelliJ IDEA2025创建SpringBoot项目的实现步骤

《IntelliJIDEA2025创建SpringBoot项目的实现步骤》本文主要介绍了IntelliJIDEA2025创建SpringBoot项目的实现步骤,文中通过示例代码介绍的非常详细,对大家... 目录一、创建 Spring Boot 项目1. 新建项目2. 基础配置3. 选择依赖4. 生成项目5.
阅读更多...
Linux线程之线程的创建、属性、回收、退出、取消方式

Linux线程之线程的创建、属性、回收、退出、取消方式

《Linux线程之线程的创建、属性、回收、退出、取消方式》文章总结了线程管理核心知识：线程号唯一、创建方式、属性设置（如分离状态与栈大小）、回收机制（join/detach）、退出方法（返回/pthr... 目录1. 线程号2. 线程的创建3. 线程属性4. 线程的回收5. 线程的退出6. 线程的取消7.
阅读更多...
创建Java keystore文件的完整指南及详细步骤

创建Java keystore文件的完整指南及详细步骤

《创建Javakeystore文件的完整指南及详细步骤》本文详解Java中keystore的创建与配置,涵盖私钥管理、自签名与CA证书生成、SSL/TLS应用,强调安全存储及验证机制,确保通信加密和... 目录1. 秘密键（私钥）的理解与管理私钥的定义与重要性私钥的管理策略私钥的生成与存储2. 证书的创建与
阅读更多...
浅析Spring如何控制Bean的加载顺序

浅析Spring如何控制Bean的加载顺序

《浅析Spring如何控制Bean的加载顺序》在大多数情况下,我们不需要手动控制Bean的加载顺序,因为Spring的IoC容器足够智能,但在某些特殊场景下,这种隐式的依赖关系可能不存在,下面我们就来... 目录核心原则：依赖驱动加载手动控制 Bean 加载顺序的方法方法 1：使用@DependsOn(最直
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2