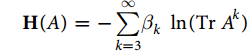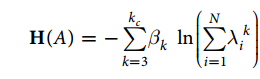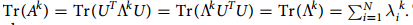本文主要是介绍通过似然分析预测丢失的边和虚假的边(潘黎明,周涛著),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
真实网络中的数据往往是不完全,存在噪音的。这时, 丢失边预测算法和虚假边的识别算法就有了用武之地。在这里提出了一种算法的框架:网络的似然可以通过预先定义好的哈密顿量来计算, 这个哈密顿量的定义考虑了网络形成的一些重要的驱动因素, 这样的话,一条没有被观测到的边的存在的“得分”可以通过计算将这条边加入已经观测到的网络中的似然来表示。
对于丢失边的预测问题,其目的是要根据已有的网路的拓扑结构和节点的信息来评估没有观测到的边的存在的可能性。对于虚假边的预测问题, 其目的是要基于已经观测到的网络的拓扑结构和节点的信息来衡量已经观测到的边的存在的可靠性。
在潘和周的论文中提出,一个观测到的网络的似然可以通过预先定义好的哈密顿量来计算得到,而对于要预测的边,把将该边添加到网络后得到的似然作为该边可能存在的得分。而这里所说的哈密顿量是根据一些合理的网络的组织原则来定义的。在这里考虑的一种被称之为是“聚类机制”(局部性原则)的普遍的原则, 这一原则表明, 如果两个节点存在共同的邻居, 那么在他们之间有很大的概率存在一条连边。 这一原则得到了三方面的证据的支持,一十大部分的网络都具有很高的簇系数, 二十基于局部性的原则建立起来的网络模型往往能够很好的再现真实网络的特性, 最重要的是,越来越多的观测揭示了真实网络生长中存在的局部性原则。(摘自周涛《链路预测》)“共同邻居相似性”在很多网络中得到了很好的体现,这说明在网络形成中更加青睐三阶环,把这一观点进一步的推广到高阶环,则得到了如下的哈密顿量的定义:
其中A是网路的邻接矩阵,TrA^k为长度为k的封闭回路数,k=1和k=2的影响是微小的。但是对于很大的k来说,TrA^k已经很难再体现局部性,所以在这里引入了一个截断值kc。事实上,即使是对于很大的网络, 小世界网络的特性依旧存在, 节点可以在很短的几步之内达到任一的另一节点。而且最近的研究表明,仅仅基于一些局部的信息也可以重构真实的网络。因此,对于很多网络一个相对较小的kc值也是很有效的。那么现在以上的哈密顿量的定义可以被重写为
在这里对邻接矩阵A进行了对角化,其中
至此, 网络的哈密顿量就定义好了。
通过最大化已经观测到的网络的哈密顿量(使用梯度上升算法)可以得到相应的参数向量\beta, 在得到了参数向量\beta之后, 对于任意的一条边,通过计算将该边添加到网络中的哈密顿量,并将其作为该边存在的“得分”来进行丢失边的预测。
为了检测丢失边预测算法的准确性,将网络中已经观测到的边分为训练集(90%)和预测集(10%),训练集的边作为已知信息而预测集的边用于测试。相似的,为了验证虚假边识别算法的准确性,要在已经观测到的网路的基础上随机的添加一些不存在的边构成训练集,这些添加的不存在的边,作为预测集。
同样的,引入了链路预测的常用的评价指标。AUC和precision。在下一篇文章中给出了算法的主要的实现代码, 通过在jazz数据上的计算,得到了预测算法的AUC值为0.98。
附
0: 实际上,链路预测算法往往会对没有观测到的边给出排序,或者计算每一条未观测到边的得分以此来表征他们存在的可能性,AUC通过考察整个未观测到的边集合评估算法的准确性, 而precision只关注分数最高或者是排名最前的L条边。
1: 关于AUC: AUC的值可以被理解为在预测集中一条随机选择的边的得分高于在不存在的边集合随机选择一条边的得分的概率。在实际应用中, 对于没有观测到的边, 我们往往计算边的得分,而不是对他们进行排序(这很费时),然后我们随机分别从预测集和不存在的边集合中各取一条边,比较他们的得分。如果在n次独立的比较中,有n'次预测集中的边得分高,有n''次它们的得分相同,那么AUC的值的计算公式如下 AUC = (n' + 0.5n'')/n。 所以, 如果所有的分数都是随机的独立同分布产生的,那么AUC的值将是0.5, 所以AUC大于0.5的程度表征了该算法准确的程度。
2: 关于Precision:精确度定义为在前L个预预测边中预测准确的比例。 例如有L’个预测准确,即根据出现的可能性从大到小排序,在top-L个中有L’个在预测集中,那么Precious = L’/ L;
3: 如何得到kc: 在前面的公式中用到了kc的值,而对于特定的网络,最佳的kc值各不相同,所以我们只能基于已有的网络来估计kc的值。在实验中,我们确切的知道预测集是什么,因此可以通过调节kc的值使得预测的结果尽量的好来获得最佳的kc,但是在实际中,我们并不知道哪些是丢失的边或者是未来可能出现的边, 我们能用的只有训练集中的边的信息。因此一个实际可行的方案就是,基于观测到的网络来学习最佳的kc, 然后将这个kc应用到接下来的算法中。比如,对于丢失边的预测来说,在将观测到的网络分为了训练集和预测集之后,我们将在训练集上学习kc的值。首先,隐藏训练集的10%记作X,然后使用的剩下的训练集的90%作为新的训练集在不同的k值下预测X, 那么在得到最好的预测效果下的k值就可以作为最佳的kc值。
这篇关于通过似然分析预测丢失的边和虚假的边(潘黎明,周涛著)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!