pymoo包NSGA2算法实现多目标遗传算法调参详细说明

本文主要是介绍pymoo包NSGA2算法实现多目标遗传算法调参详细说明，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1.定义待求解问题

1.0定义问题的参数说明

• 1.0.0 求解问题必须设置在def _evaluate(self, x, out, *args, **kwargs)函数中

• 1.0.1 问题必须用 out[“F”] = [f1, f2] 包裹起来

• 1.0.2 约束条件也必须用 out[“G”] = [g3] 包裹起来

• 1.0.3 def __init__(self):里需要定义以下参数

• n_var定义的是待求解的 $X$变量数量
• n_obj定义的是待求解 $f$ 问题数量
• n_ieq_constr定义的是约束条件的数量
• xl定义的是待求解的$X$参数的下限
• xu定义的是待求解的$X$参数的上限
• f1,f2定义问题
• g1,g2定义约束条件

• 1.0.4 约束条件的g以不等式形式写明 会按照小于等于0 进行选择

import numpy as np
from pymoo.core.problem import ElementwiseProblemclass MyProblem(ElementwiseProblem):def __init__(self):super().__init__(n_var=2, # X 变量数量n_obj=2, # f 问题数n_ieq_constr=1,# g 约束条件数量xl=np.array([-2,-2]), # X 自变量下限xu=np.array([2,2])# X 自变量上限) def _evaluate(self, x, out, *args, **kwargs):# 待求解函数 f1 = np.cos(x[0]+x[1]) #100 * (x[0]**2 + x[1]**2) f2 = np.sin(x[0]+x[1]) #(x[0]-1)**2 + x[1]**2# f3 = (abs(x[0])<0.3)+(abs(x[1])<0.5)# 约束条件会选择 <= 0 的选择# g1 = 2*(x[0]-0.1) * (x[0]-0.9) / 0.18# g2 = - 20*(x[0]-0.4) * (x[0]-0.6) / 4.8# g3 = ((x[0]**2)<0.5)+((x[1]**2)>0.3)g3 = x[0]-0.7 #+(abs(x[1])<0.3)out["F"] = [f1, f2] #待求解问题#out["G"] = [g1, g2,g3] #约束条件out["G"] = [g3] #约束条件problem = MyProblem()

2.调用NSGA2的算法包设置参数

2.1 NSGA2函数的参数设置

• pop_sizez种群数量
• n_offsprings每代的数量
• sampling#抽样设置
• crossove()交叉配对设置
• • prob交叉配对的概率设置
• • eta
• mutation()变异译概率
• • prob是变异的概率设置
• • eta
• eliminate_duplicates我们启用重复检查（“eliminate_duplicates=True”），确保交配产生的后代在设计空间值方面与自身和现有种群不同。

from pymoo.algorithms.moo.nsga2 import NSGA2
from pymoo.operators.crossover.sbx import SBX
from pymoo.operators.mutation.pm import PM
from pymoo.operators.sampling.rnd import FloatRandomSampling,IntegerRandomSampling,BinaryRandomSamplingalgorithm = NSGA2(pop_size=90, # z种群数量n_offsprings=100, # 每代的数量sampling= FloatRandomSampling(), #抽样设置#交叉配对crossover=SBX(prob=0.9 #交叉配对概率, eta=15), #配对效率#变异mutation=PM(prob=0.8 #编译概率,eta=20),# 配对效率eliminate_duplicates=True
)

3.定义迭代次数90次

from pymoo.termination import get_terminationtermination = get_termination("n_gen", 90)

4.求解最帕累托最优解集的参数x向量

from pymoo.optimize import minimizeres = minimize(problem,algorithm,termination,seed=1,save_history=True,verbose=True)X = res.X # 求解出来的参数
F = res.F # 帕累托最优解集

4.2 查看输出的X的解

array([[-1.22983903, -0.3408983 ],[-1.17312926, -1.9683635 ],[-1.62815244, -1.25867184],[-1.59459202, -1.24720921],[-0.85812605, -0.86104326],[ 0.14217774, -1.79408273],[-1.16038493, -0.45298884],[-1.30857014, -0.53215836],[-0.99480251, -1.0484723 ],[-1.17506923, -0.83512127],[-1.12330204, -1.13340585],[-1.02395611, -1.33764674],[-0.99658648, -0.88776711],[-0.87963539, -0.86581268],[-1.59330301, -0.09593218],[-1.89860429, -1.07240541],[-0.92025241, -0.88515559],[-1.89221588, -1.02590525],[-1.15977198, -0.61984559],[-1.23391136, -1.89214062],[-1.08575639, -1.1960931 ],[-1.8422881 , -1.17730121],[-1.97907088, -0.67847822],[-1.19339619, -1.30837703],[-1.81657534, -0.6468284 ],[-1.34872892, -1.1691978 ],[-1.70461135, -1.08101794],[-1.28766298, -0.92085304],[-1.10488217, -1.16702018],[-1.45199598, -0.92807938],[-1.83785271, -0.26933177],[-1.10292853, -1.0760453 ],[-1.97460715, -1.02344251],[-1.92346673, -1.17730121],[-1.35716933, -0.9513154 ],[-1.07370789, -1.16339584],[-1.61844778, -0.54832033],[-1.69262569, -1.29666833],[-1.1205858 , -1.9683635 ],[-1.32886108, -1.09105746],[-0.87963539, -0.85896725],[-1.17319829, -1.50153054],[-1.63954555, -1.28599005],[-0.92662448, -0.93538073],[-1.29072744, -0.82715754],[-1.72496415, -1.22313643],[-1.70410919, -1.36171497],[-1.57300848, -1.04123091],[-1.81522276, -0.66364657],[-1.28643454, -1.14856238],[-1.13870379, -0.8286136 ],[-1.60254074, -1.21320856],[-1.3972806 , -0.68146238],[-1.37242908, -0.92807938],[-1.29950364, -0.37689045],[-1.32237812, -1.09105746],[-1.59549137, -1.35399596],[-0.86920703, -1.22313643],[-1.38180886, -1.34157915],[-1.46024398, -1.24232167],[-1.12485534, -1.47579521],[-1.24917941, -1.2408934 ],[-1.6174287 , -1.02798238],[-1.46214609, -0.68146238],[-0.89315598, -0.95504252],[-1.2693953 , -1.07649403],[-1.31640451, -1.32237493],[-1.2414329 , -1.15952844],[-1.10828403, -0.80474544],[-1.06864911, -0.83165391],[-1.83785271, -1.1960931 ],[-1.03382957, -1.50125804],[-1.81678927, -0.71106355],[-1.12485534, -1.50226124],[-1.14170746, -1.05251568],[-0.37583973, -1.94856256],[-1.19888652, -0.86892885],[-1.44462396, -0.94172587],[-1.57293402, -1.19861388],[-1.7873066 , -1.04123091],[-1.19339619, -0.74337764],[-1.41439116, -0.77744839],[-1.03394747, -1.65557748],[-1.29621172, -0.30606688],[-0.85812605, -1.09549174],[-1.31640451, -1.39906326],[-1.36337969, -1.03256822],[-1.59459202, -1.20585082],[-1.10292853, -1.02523266],[-1.85491578, -0.88327578]])

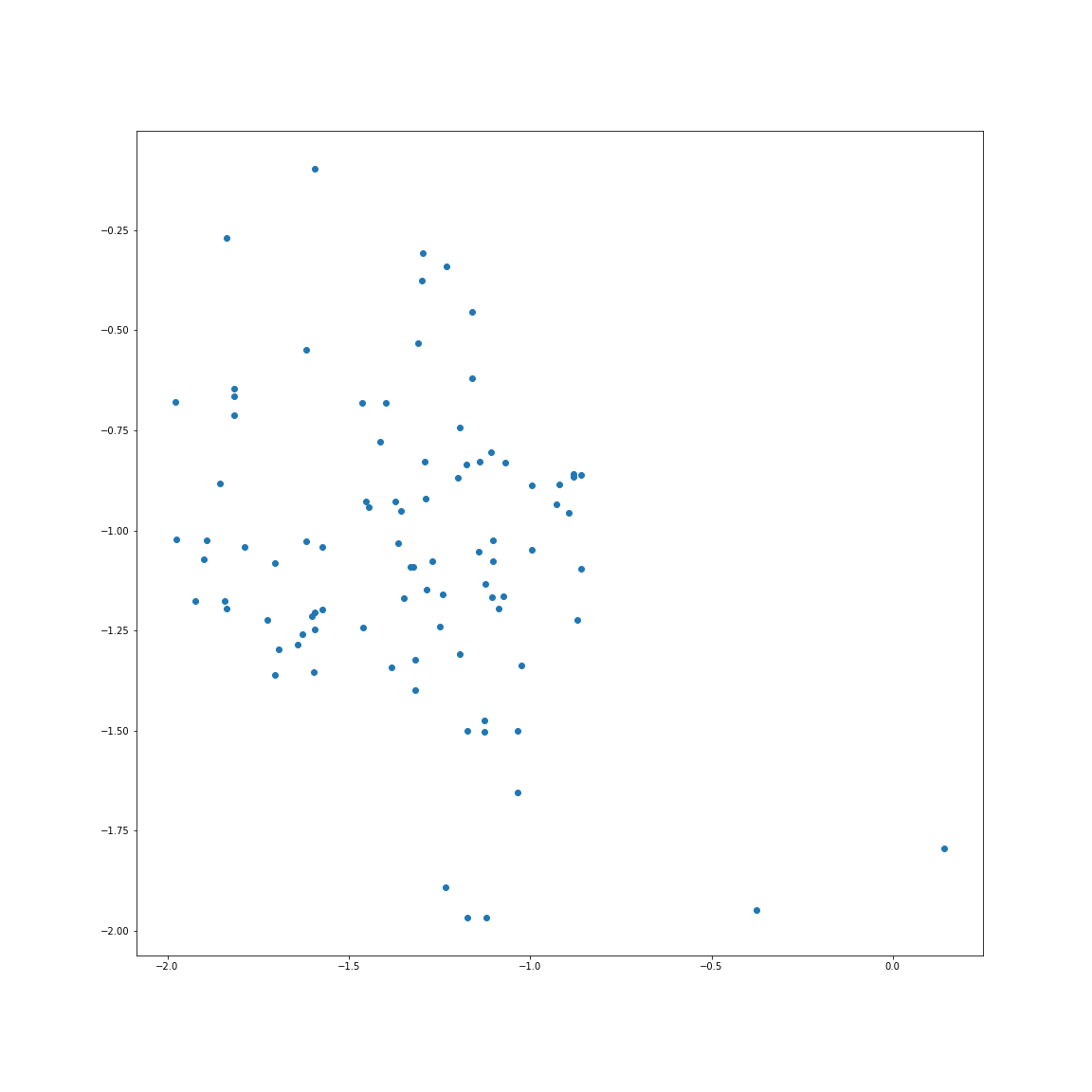
5.帕累托最优解集的X向量参数最优解集分布

import matplotlib.pyplot as plt 
plt.figure(figsize=(16,16))
plt.scatter(X[:,0],X[:,-1])

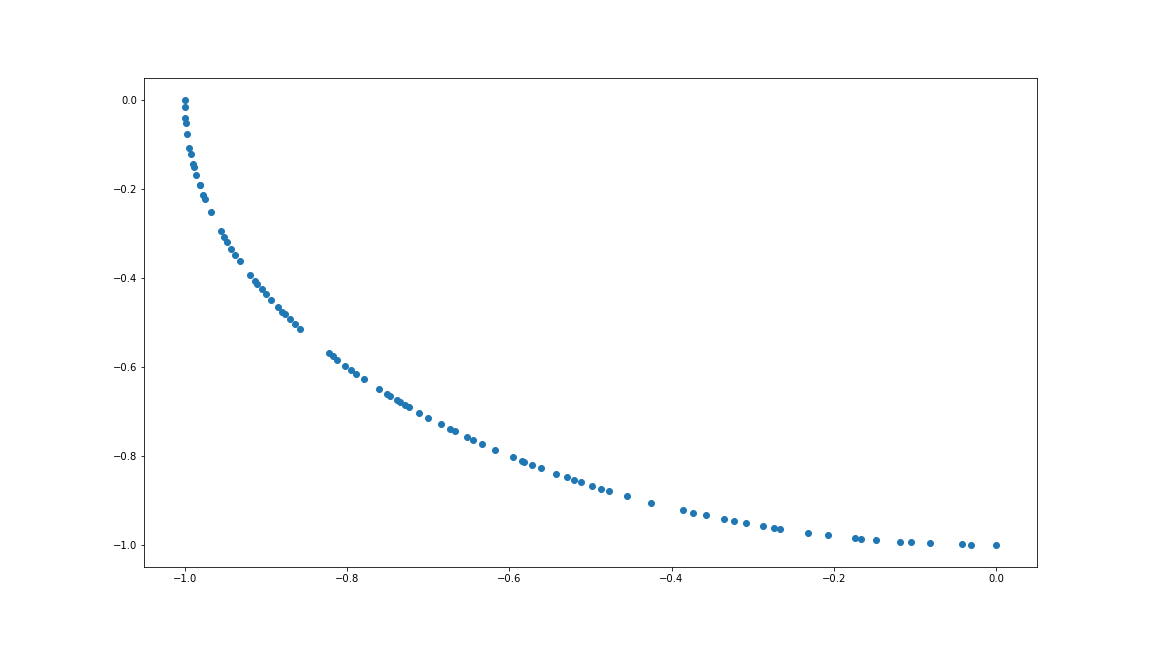
6.画出帕累托前沿

import matplotlib.pyplot as plt 
plt.figure(figsize=(16,9))
plt.scatter(F[:,0],F[:,-1])
plt.savefig("NSGA2demo帕累托前沿.png")

这篇关于pymoo包NSGA2算法实现多目标遗传算法调参详细说明的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---