本文主要是介绍10.10泊松、指数、伽马分布的理解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
泊松定理、泊松分布
泊松定理就是描述在T段时间内每时每刻一直进行一个实验,这个实验成功的概率由t段时间总的成功期望次数决定,就是给二项分布加了个时间
泊松分布可用来描述某段时间来电次数的分布,电话台收到的呼叫数,商城的顾客数,机场的航班起落次数。是单位时间(单位面积,单位产品)上稀有事件发生的次数,langmuda为该稀有事件发生的强度
根据单位时间的定义(划分)不同(可以是一秒,一分钟也可以是一天,一个月),强度朗姆达也不同,但描述的意义就是这一个所划分的单位时间中发生的平均总次数,然后以此得到(模拟)这段单位时间上发生的所有可能性的概率,并可以预测下个单位时间上发生的所有可能性(数量)的概率

泊松流
泊松分布只有一个参数,就是强度,即单位时间上发生次数的平均总次数
泊松流有两个参数,一个是强度,一个是时间
即泊松分布是泊松流第二个参数时间为1的情形
其都是用来表示在一段时间t内不断实验,然后表述这段时间上发生的总次数
只不过泊松分布是单位时间,泊松流是任意时间长度
但参数总归是要已知的,可以说是事先确定好强度与时间段,或者可以根据取样的数据来反推
但实际上泊松流还可以是一个泊松分布,即把“单位时间”变了,定义这个t时间为单位时间,那就是新的泊松分布,只不过强度变了,设原来的单位时间客观长a,现在这个泊松流的时间为ba,b为任意不为0实数,也就是由原来的基础泊松分布(单位时间为a),定义出了新的泊松分布(单位时间为b*a)。
单位时间发生变化,则强度也会发生变化,因为强度是描述单位时间上发生的总次数,现在的总次数就是说由几个原来的单位时间的平均总次数组合在一起形成的新总次数,即朗姆达乘t,t为该泊松流持续时间,即假设原泊松分布的单位时间就为单位1,且朗姆达为在单位1时间上发生的平均总次数
就是知道一个泊松分布,确定其单位时间的意义,然后确定泊松流的持续时间是由多少个这个单位组成的,就可以用新泊松分布的表达式来表示
所以泊松流的表达式就是可以用泊松分布的表达式来表达,就是强度为朗姆达*t的泊松分布
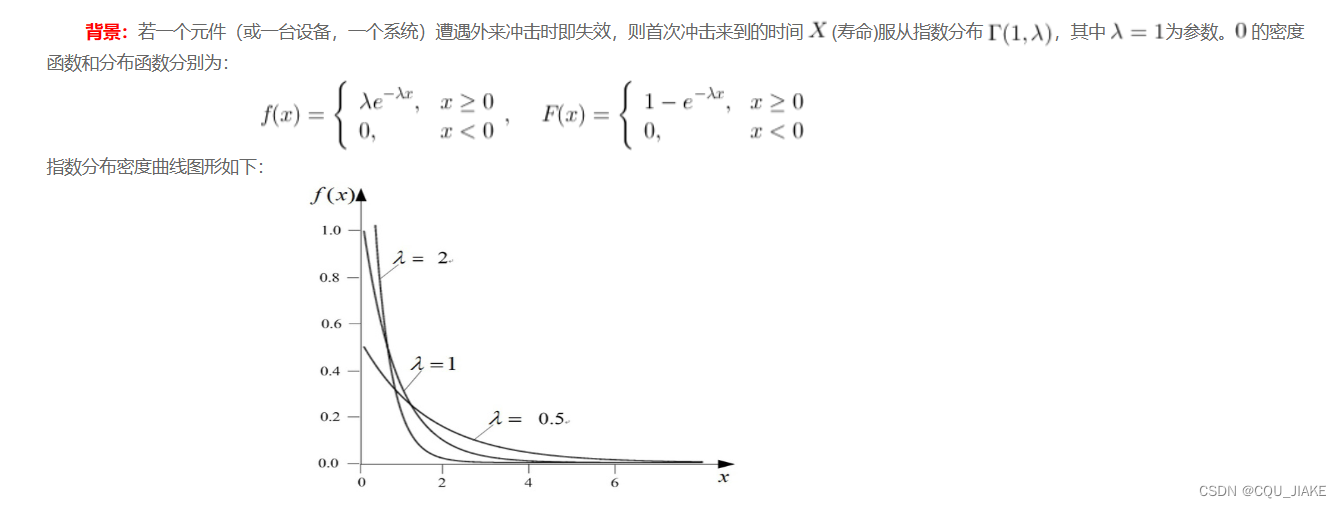
指数分布
指数分布用来描述相邻次数之间的等待时间,
和泊松分布密切相关,就是在一段时间t内不断实验,那么两次实验成功的时间间隔的分布
如果问寿命,
把实验当成出问题,每时每刻都有可能出问题,那么寿命不大于T,就是1-寿命大于T,寿命大于T就说明在0~T的时间(一个泊松流)内不断尝试出问题,但这段时间一直没有问题(在这一段泊松流里事件没有发生),即成功的次数为0 (首先还是要标定一个单位时间的泊松分布,才会有泊松流的概念,才可以有指数分布),那就会使寿命至少为t,再让总体减掉它,就是寿命不大于t的概率和,求导就是寿命为t的概率
理解无记忆性就是,泊松流之间是相互独立的,泊松流之间互不影响
指数分布的参数只有一个就是朗姆达,为单位时间上泊松分布的强度;
描述的是t,即从实验开始(或是上一次实验结束),遇到第一次发生(或下一次实验开始)的等待的时间
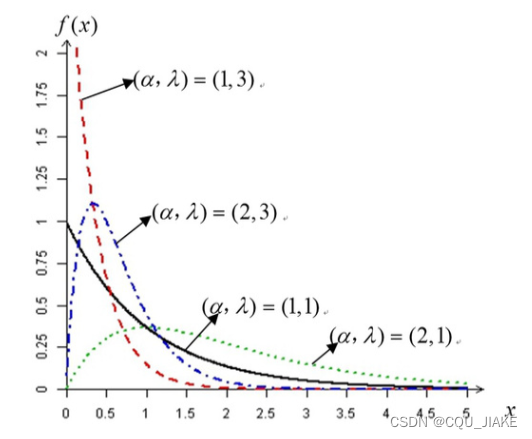
伽马分布是从开始到发生n次的等待时间,有两个参数,一个是要发生的次数,一个是单位时间上发生的强度
伽马分布



总结
串起来的思路就是
单位时间上不断实验,实验的成功次数满足泊松分布
然后由这个单位时间可以标定任意长度时间,那么任意长度时间上实验成功的次数就是泊松流
在任意长度时间的基础上,给定一段时间的泊松流,那么这个泊松流里相邻两次事件的发生时间间隔满足指数分布
如果把事件理解为出一次问题,那么出一次问题就报废(即从0->1)的间隔时间(理解为寿命)分布为指数分布
出两次,n次问题才报废,则为伽马分布
理解一个案例,打电话
单位时间上接到的电话平均总次数为朗姆达,强度,泊松分布
(就是每分钟接到的电话数)
那么t时间上接到的平均总次数为泊松流
(由每分钟所衡量出的任意时间里接到的电话)
假设在打电话期间,如果没有接到新电话,就会一直通这一个电话,那么每个电话的通话时长就是指数分布
(接到电话后的0~10min的泊松流内无新电话打来,即通话时间不少于10min)
//通话时长在10分钟以上,就可以理解为在0~t,t>10的泊松流内,一直没有新电话(事件)发生
如果接到新电话,但是只是一个电话就不管,只有累计到n个新电话才会结束这个电话,那么每个电话的通话时长就是伽马分布

这篇关于10.10泊松、指数、伽马分布的理解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







