《Ray Tracing in One Weekend》阅读笔记 - 9、电介质

2023-10-10 14:50
文章标签 笔记 阅读 one ray tracing weekend 电介质

本文主要是介绍《Ray Tracing in One Weekend》阅读笔记 - 9、电介质，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

    像水、玻璃和钻石这样的透明材料是电介质，当光击中他们时，光线会分成反射光线和折射（透射）光线。我们将随机选择当前光线是反射还是折射，并且每次交互只产生一个散射光线。

 

9.1 折射

    最难debug的部分是折射光线。作者先让所有的光线都变成折射光线，在这个项目中，作者尝试将两个玻璃球放在场景中（左边两个）：

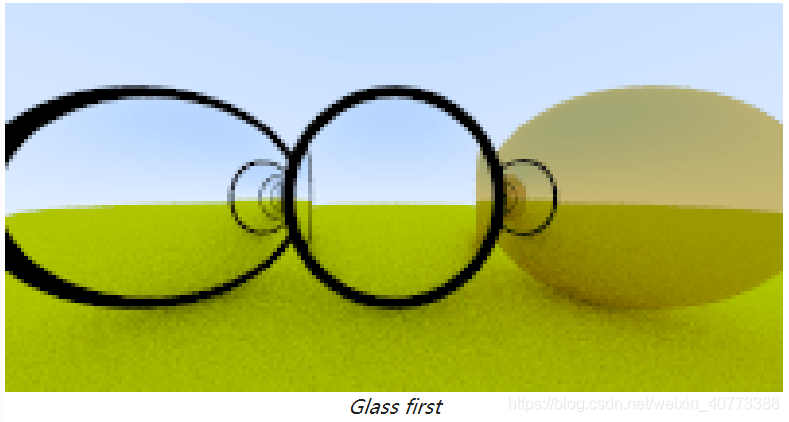
    这个看上很明显不符合现实，现实中透过球体我们应该看到上下颠倒的影像，并且没有奇怪的黑边。 I just printed out the ray straight through the middle of the image and it was clearly wrong. That often does the job.

 

 

9.2 斯涅尔定律

    折射用Snell定律来描述：

 

  • θ是入射光线与表面法向量的夹角，θ' 是折射光线与折射面的表面法向量的夹角。
  • η（读作“eta”）入射面的介质的折射率，η'是折射面的介质的折射率（通常空气= 1.0，玻璃= 1.3-1.7，钻石= 2.4）。

    如下图所示：

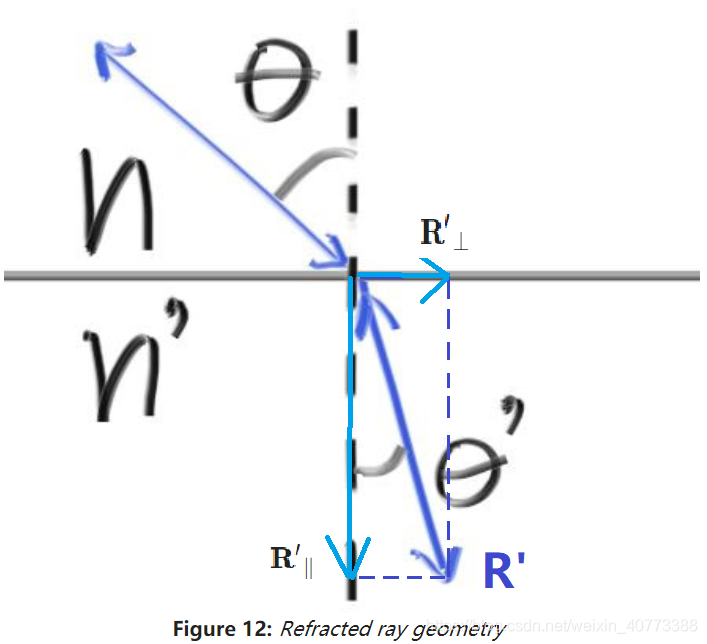
根据上式，计算折射角的正弦值：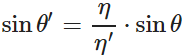

 

我们可以将折射光线R分解为两个向量：平行于n'的分量和垂直于n'的分量，如下式所示：

 

由向量的计算方法，我们可以计算两者：（作图计算可证）

 

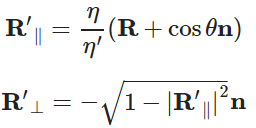
上式中的θ还没求出。我们都知道向量的点积可以这么计算：a ⋅ b = |a||b|cosθ，当a、b均为单位向量时，有：a ⋅ b = cosθ，所以我们可以重写上面的式子：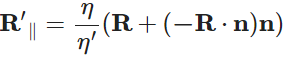

 

把上面的式子合在一起，我们可以写一个函数refract来计算R'：

// 网页上的代码 vec3.h
vec3 refract(const vec3& uv, const vec3& n, double etai_over_etat) {auto cos_theta = dot(-uv, n);vec3 r_out_parallel =  etai_over_etat * (uv + cos_theta*n);vec3 r_out_perp = -sqrt(1.0 - r_out_parallel.length_squared()) * n;return r_out_parallel + r_out_perp;
}

而总是发生折射的介电材料dielectric类的结构为：

  1. 包含的成员变量：ref_idx：物体外部介质的折射率η和物体内部折射率η'之比：η/η'。
  2. 拥有的方法：
    1. 带参初始化
    2. 判断是否散射（如果是，返回散射的光线和颜色）
      1. 设置衰减率attenuation为全反射、不衰减
      2. 判断光线是从物体外部照射还是从物体内部照射，设置此时的etai_over_etat
      3. 将入射光线方向转化为单位长度的向量
      4. 计算折射方向
      5. 生成散射光线，返回true
// 网页上的代码 material.h
class dielectric : public material {public:dielectric(double ri) : ref_idx(ri) {}virtual bool scatter(const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered) const {attenuation = color(1.0, 1.0, 1.0);double etai_over_etat;if (rec.front_face) {etai_over_etat = 1.0 / ref_idx;} else {etai_over_etat = ref_idx;}vec3 unit_direction = unit_vector(r_in.direction());vec3 refracted = refract(unit_direction, rec.normal, etai_over_etat);scattered = ray(rec.p, refracted);return true;}double ref_idx;
};

运行的结果如下图所示：

 

 

9.3 全内反射

    上面的图片看起来肯定不对。一个棘手的实际问题是，当光线在折射率较高的材料中时，Snell's law没有实数解，因此不可能发生折射。让我们回到Snell's law的推导：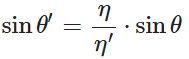

 

如果光线从玻璃内照射到空气中(η=1.5 and η′=1.0)：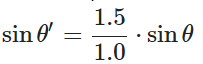

 

 由于sinθ的值一定小于1，如果1.5sinθ'>1.0，则上面的等式无解，那么玻璃将无法反射。因此必须考虑这种情况并反射光线：

// 网页上的代码 material.h
if(etai_over_etat * sin_theta > 1.0) {// Must Reflect...
}
else {// Can Refract...
}

    在这里所有的光都被反射，并且因为在实践中通常发生在固体内部，这被称为“全内反射”。这就是为什么当你在水中的时候，水气边界有时候像一面完美的镜子。

    我们可以用三角函数 的性质来解出sinθ：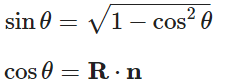

// 网页上的代码 material.h
double cos_theta = fmin(dot(-unit_direction, rec.normal), 1.0);
double sin_theta = sqrt(1.0 - cos_theta*cos_theta);
if(etai_over_etat * sin_theta > 1.0) {// Must Reflect...
}
else {// Can Refract...
}

    介电材料总是折射(可能时)为:

// 网页上的代码 material.h
class dielectric : public material {public:dielectric(double ri) : ref_idx(ri) {}virtual bool scatter(const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered) const {attenuation = color(1.0, 1.0, 1.0);double etai_over_etat = (rec.front_face) ? (1.0 / ref_idx) : (ref_idx);vec3 unit_direction = unit_vector(r_in.direction());double cos_theta = fmin(dot(-unit_direction, rec.normal), 1.0);double sin_theta = sqrt(1.0 - cos_theta*cos_theta);if (etai_over_etat * sin_theta > 1.0 ) {vec3 reflected = reflect(unit_direction, rec.normal);scattered = ray(rec.p, reflected);return true;}vec3 refracted = refract(unit_direction, rec.normal, etai_over_etat);scattered = ray(rec.p, refracted);return true;}public:double ref_idx;
};

光线的衰减率总是1——玻璃表面不吸收任何光线。如果我们使用以下参数：

// 网页代码 main.cc
world.add(make_shared<sphere>(point3(0,0,-1), 0.5, make_shared<lambertian>(color(0.1, 0.2, 0.5))));
world.add(make_shared<sphere>(point3(0,-100.5,-1), 100, make_shared<lambertian>(color(0.8, 0.8, 0.0))));
world.add(make_shared<sphere>(point3(1,0,-1), 0.5, make_shared<metal>(color(.8, .6, .2), 0.0)));
world.add(make_shared<sphere>(point3(-1,0,-1), 0.5, make_shared<dielectric>(1.5)));

    我们将得到：

 

 

9.4 Schlick近似

    现在，真正的玻璃具有随角度变化的反射率——从一个陡峭的角度看一扇窗户，它就变成了一面镜子。有一个很大的丑陋的方程描述这个，但几乎每个人都使用一个便宜的和有令人惊讶的准确性的多项式近似，由Christophe Schlick提出:

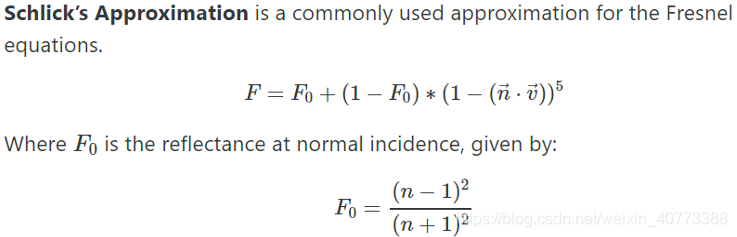
(图片来源：https://graphicscompendium.com/raytracing/11-fresnel-beer)

 

（图片来源：https://en.wikipedia.org/wiki/Schlick%27s_approximation）（wikipedia的解释更清楚一点）

// 网页上的代码 material.h -- Schlick approximation
double schlick(double cosine, double ref_idx) {auto r0 = (1-ref_idx) / (1+ref_idx);r0 = r0*r0;return r0 + (1-r0)*pow((1 - cosine),5);
}

    这样就得到了完整的玻璃材料：

// 网页上的代码 material.h
class dielectric : public material {public:dielectric(double ri) : ref_idx(ri) {}virtual bool scatter(const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered) const {attenuation = color(1.0, 1.0, 1.0);double etai_over_etat = (rec.front_face) ? (1.0 / ref_idx) : (ref_idx);vec3 unit_direction = unit_vector(r_in.direction());double cos_theta = fmin(dot(-unit_direction, rec.normal), 1.0);double sin_theta = sqrt(1.0 - cos_theta*cos_theta);if (etai_over_etat * sin_theta > 1.0 ) {vec3 reflected = reflect(unit_direction, rec.normal);scattered = ray(rec.p, reflected);return true;}double reflect_prob = schlick(cos_theta, etai_over_etat);if (random_double() < reflect_prob){vec3 reflected = reflect(unit_direction, rec.normal);scattered = ray(rec.p, reflected);return true;}vec3 refracted = refract(unit_direction, rec.normal, etai_over_etat);scattered = ray(rec.p, refracted);return true;}public:double ref_idx;
};

 

 

9.5 制作中空玻璃球

    对于电介质体，有一个有趣且简单的技巧：如果你使用负半径，几何形状几乎不受影响，但表面法线指向内。这可以用来作为一个气泡，做成一个中空的玻璃球：

// 网页上的代码 main.cc
world.add(make_shared<sphere>(point3(0,0,-1), 0.5, make_shared<lambertian>(color(.1, .2, .5))));
world.add(make_shared<sphere>(point3(0,-100.5,-1), 100, make_shared<lambertian>(color(.8,.8,0.))));
world.add(make_shared<sphere>(point3(1,0,-1), 0.5, make_shared<metal>(color(.8, .6, .2), 0.3)));
world.add(make_shared<sphere>(point3(-1,0,-1), 0.5, make_shared<dielectric>(1.5)));
world.add(make_shared<sphere>(point3(-1,0,-1), -0.45, make_shared<dielectric>(1.5)));

我们将会得到：

 

 

 

 

 

 

 

 

这篇关于《Ray Tracing in One Weekend》阅读笔记 - 9、电介质的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/181161。

相关文章

JAVA智听未来一站式有声阅读平台听书系统小程序源码

JAVA智听未来一站式有声阅读平台听书系统小程序源码

智听未来，一站式有声阅读平台听书系统 🌟&nbsp;开篇：遇见未来，从“智听”开始 在这个快节奏的时代，你是否渴望在忙碌的间隙，找到一片属于自己的宁静角落？是否梦想着能随时随地，沉浸在知识的海洋，或是故事的奇幻世界里？今天，就让我带你一起探索“智听未来”——这一站式有声阅读平台听书系统，它正悄悄改变着我们的阅读方式，让未来触手可及！ 📚&nbsp;第一站：海量资源，应有尽有 走进“智听
阅读更多...
【学习笔记】 陈强-机器学习-Python-Ch15 人工神经网络（1）sklearn

【学习笔记】 陈强-机器学习-Python-Ch15 人工神经网络（1）sklearn

系列文章目录 监督学习：参数方法 【学习笔记】 陈强-机器学习-Python-Ch4 线性回归 【学习笔记】 陈强-机器学习-Python-Ch5 逻辑回归 【课后题练习】 陈强-机器学习-Python-Ch5 逻辑回归（SAheart.csv） 【学习笔记】 陈强-机器学习-Python-Ch6 多项逻辑回归 【学习笔记 及 课后题练习】 陈强-机器学习-Python-Ch7 判别分析 【学
阅读更多...
系统架构师考试学习笔记第三篇——架构设计高级知识（20）通信系统架构设计理论与实践

系统架构师考试学习笔记第三篇——架构设计高级知识（20）通信系统架构设计理论与实践

本章知识考点：         第20课时主要学习通信系统架构设计的理论和工作中的实践。根据新版考试大纲,本课时知识点会涉及案例分析题(25分),而在历年考试中,案例题对该部分内容的考查并不多,虽在综合知识选择题目中经常考查,但分值也不高。本课时内容侧重于对知识点的记忆和理解,按照以往的出题规律,通信系统架构设计基础知识点多来源于教材内的基础网络设备、网络架构和教材外最新时事热点技术。本课时知识
阅读更多...
论文阅读笔记: Segment Anything

论文阅读笔记: Segment Anything

文章目录 Segment Anything摘要引言任务模型数据引擎数据集负责任的人工智能 Segment Anything Model图像编码器提示编码器mask解码器解决歧义损失和训练 Segment Anything 论文地址: https://arxiv.org/abs/2304.02643 代码地址:https://github.com/facebookresear
阅读更多...
数学建模笔记—— 非线性规划

数学建模笔记—— 非线性规划

数学建模笔记—— 非线性规划 非线性规划1. 模型原理1.1 非线性规划的标准型1.2 非线性规划求解的Matlab函数 2. 典型例题3. matlab代码求解3.1 例1 一个简单示例3.2 例2 选址问题1. 第一问 线性规划2. 第二问 非线性规划 非线性规划 非线性规划是一种求解目标函数或约束条件中有一个或几个非线性函数的最优化问题的方法。运筹学的一个重要分支。2
阅读更多...
【C++学习笔记 20】C++中的智能指针

【C++学习笔记 20】C++中的智能指针

智能指针的功能 在上一篇笔记提到了在栈和堆上创建变量的区别，使用new关键字创建变量时，需要搭配delete关键字销毁变量。而智能指针的作用就是调用new分配内存时，不必自己去调用delete，甚至不用调用new。 智能指针实际上就是对原始指针的包装。 unique_ptr 最简单的智能指针，是一种作用域指针，意思是当指针超出该作用域时，会自动调用delete。它名为unique的原因是这个
阅读更多...
查看提交历史 —— Git 学习笔记 11

查看提交历史 —— Git 学习笔记 11

查看提交历史 查看提交历史 不带任何选项的git log-p选项--stat 选项--pretty=oneline选项--pretty=format选项git log常用选项列表参考资料 在提交了若干更新，又或者克隆了某个项目之后，你也许想回顾下提交历史。 完成这个任务最简单而又有效的 工具是 git log 命令。 接下来的例子会用一个用于演示的 simplegit
阅读更多...
记录每次更新到仓库 —— Git 学习笔记 10

记录每次更新到仓库 —— Git 学习笔记 10

记录每次更新到仓库 文章目录 文件的状态三个区域检查当前文件状态跟踪新文件取消跟踪（un-tracking）文件重新跟踪（re-tracking）文件暂存已修改文件忽略某些文件查看已暂存和未暂存的修改提交更新跳过暂存区删除文件移动文件参考资料 咱们接着很多天以前的 取得Git仓库 这篇文章继续说。 文件的状态 不管是通过哪种方法，现在我们已经有了一个仓库，并从这个仓
阅读更多...
忽略某些文件 —— Git 学习笔记 05

忽略某些文件 —— Git 学习笔记 05

忽略某些文件 忽略某些文件 通过.gitignore文件其他规则源如何选择规则源参考资料 对于某些文件，我们不希望把它们纳入 Git 的管理，也不希望它们总出现在未跟踪文件列表。通常它们都是些自动生成的文件，比如日志文件、编译过程中创建的临时文件等。 通过.gitignore文件 假设我们要忽略 lib.a 文件，那我们可以在 lib.a 所在目录下创建一个名为 .gi
阅读更多...
取得 Git 仓库 —— Git 学习笔记 04

取得 Git 仓库 —— Git 学习笔记 04

取得 Git 仓库 —— Git 学习笔记 04 我认为， Git 的学习分为两大块：一是工作区、索引、本地版本库之间的交互；二是本地版本库和远程版本库之间的交互。第一块是基础，第二块是难点。 下面，我们就围绕着第一部分内容来学习，先不考虑远程仓库，只考虑本地仓库。 怎样取得项目的 Git 仓库？ 有两种取得 Git 项目仓库的方法。第一种是在本地创建一个新的仓库，第二种是把其他地方的某个
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2