极大极小搜索Alpha-Beta搜索

极大极小搜索&Alpha-Beta搜索

本文为小编关于极大极小搜索和Alpha-Beta剪枝方面的学习笔记

极大极小搜索

1. 极大极小搜索算法思想

• 基于博弈树，二人博弈游戏的目标是寻找方案使得自己的利益最大化。假设玩家A,B足够聪明，A总是能选择最有利于自己的方案；玩家B总能选择最不利于A的方案。对弈双方选择做法的时候尽量让棋局朝着有利于自己的方向转化，在博弈树上的不同层遵从不同的选择标准。

2. 算法执行顺序

• 自底向上。先把搜索树画到我们可以承受的深度，然后逐层往上取最大最小值回溯。

3. 算法执行过程

算法执行过程见下图，圆圈是玩家A，方块是玩家B，数值越大对玩家A越有利，反之对玩家B有利：

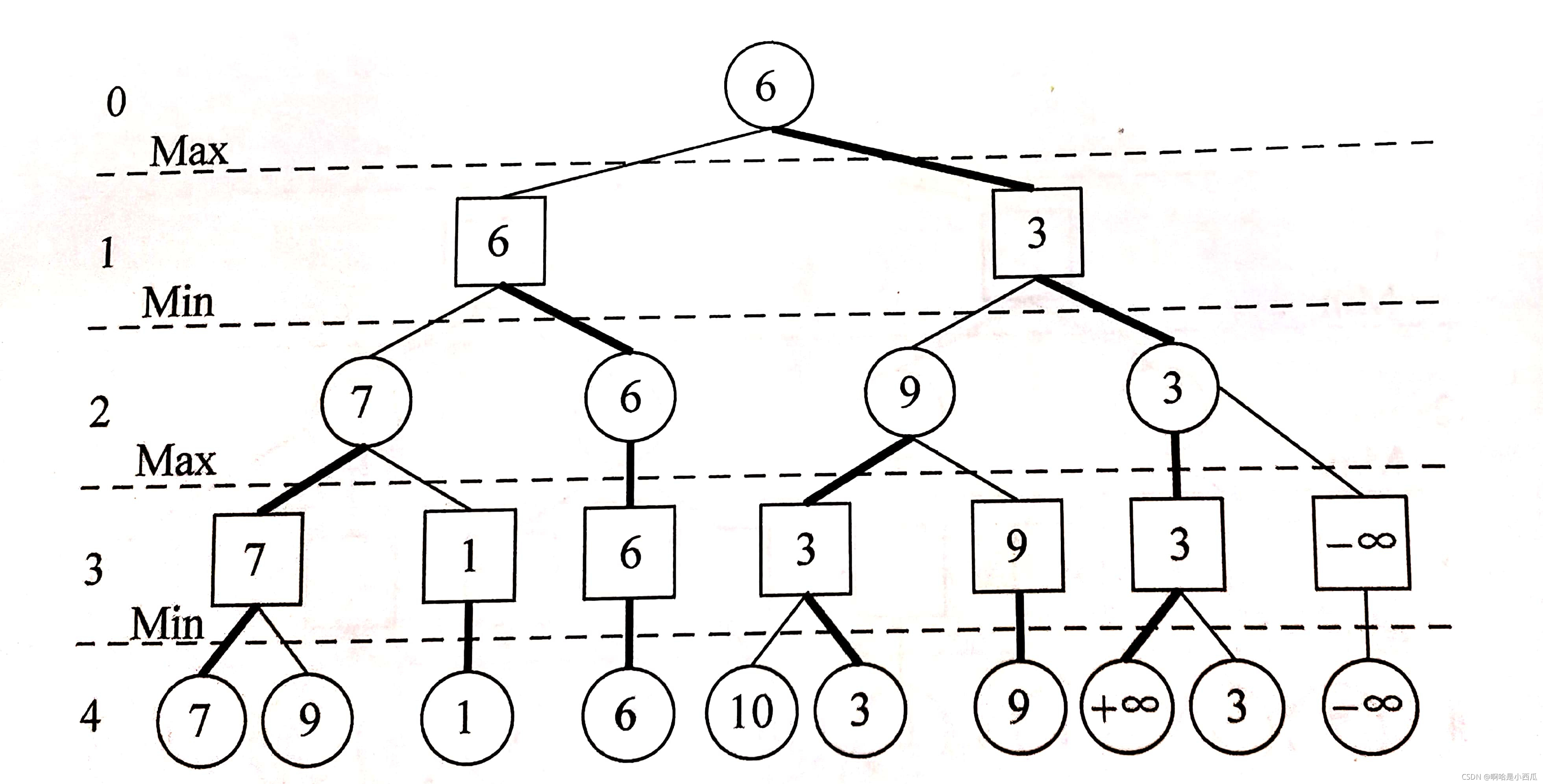
1. 以最左左子树为例，在第三层对于玩家B来说当前局面7和9两个选择中，7最小，故玩家B选择7这一着法；
2. 在第二层，对于玩家A来说7和1两个选择中，7最大，故玩家A选择7这一着法；
3. 在第一层，对于玩家B来说7和6两个选择中，6最小，故玩家B选择6这一着法；
4. 在根节点，对于玩家A来说，6最大，故玩家A选择6这一着法。

4. 注意

• 极大极小搜索算法非常依赖于评估函数的准确度，如果评估函数不准确，则会导致经过极大极小搜索后得到的方案是局部最优而不是全局最优。
• 进过多次游戏后才能逼近或达到纳什平衡，因为第一次游戏大家不知道自己或对方是不是完美决策者。

纳什平衡：是双方在熟知游戏规则下做出的最优决定。

Alpha-Beta搜索

目标：解决极大极小值冗余。

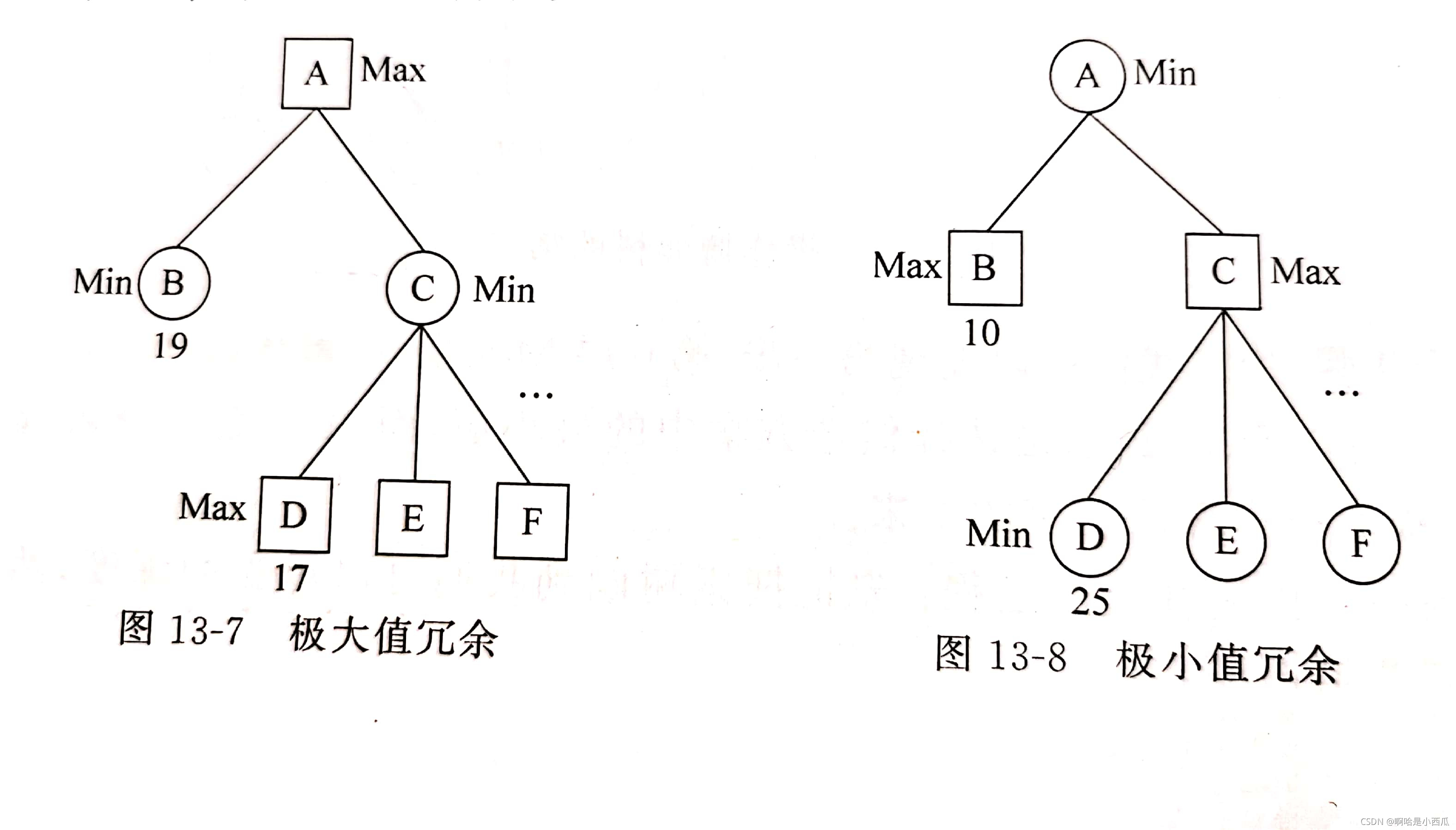
1. 极大值冗余

如图13-7 为极大值冗余。

• 以C为例子，C的父节点A要最大值儿子，但C节点本身要最小值儿子；C节点的第一个儿子是17，所以C节点的值只会小于等于17，但是C节点的兄弟B节点的最小值是19，所以此时C节点再去搜索儿子E,F的值就很多余。

小编根据对极大值冗余的理解进行总结：极大值冗余是min层节点对没有搜素价值的max层子节点（极大值）进行搜索。

2. 极小值冗余

如图13-8为极小值冗余

• 还是以C为例，C的父节点要小值儿子，但是C节点本身要大值儿子，C的第一个儿子值是25，所以C节点的取值只会大于或等于25，比兄弟节点B的最大值还大，所以C节点再去搜E和F也很多余。

小编根据对极小值冗余的理解进行总结：极小值冗余是max层节点对没有搜素价值的min层子节点（极小值）进行搜索。

3. 极大极小值冗余的克星——Alpha-Beta剪枝

Alpha-Beta剪枝就是剪去极大极小值冗余中类似E,F节点的操作。

1）执行顺序：自底向上，从左到右。

2）初始状态：非叶子节点搜索区间为[-∞，+∞]

3）Alpha-Beta剪枝优势

• 虽然结果和极大极小搜索所得结果相同，但由于剪去了不影响最终决定的分枝，相同时间内Alpha-Beta剪枝搜索的深度可以达到极大极小算法的两倍多。

4）剪枝过程

α是下界，β是上界，每个非叶节点的初始搜索区间为[-∞，+∞]，在剪枝过程中，max层不希望自己变得更小，所以会修改自己的下界α；min层不希望自己变得更大，所以修改自己的上界β。

1. Alpha剪枝：min层节点的子节点如果小于等于其前驱max层节点的α值，则可终止该min节点以下的搜索过程；
2. Beta剪枝：max层节点的子节点如果大于等于其前驱min层节点的β值，则可终止该max节点以下的搜索过程。

总结来说就是：

1. min层节点在已知自己不被父节点选中的情况下，剪掉了其在max层子节点不必要的α值的更新；
2. max层节点在已知自己不被父节点选中的情况下，剪掉了其在min层子节点不必要的β值的更新。

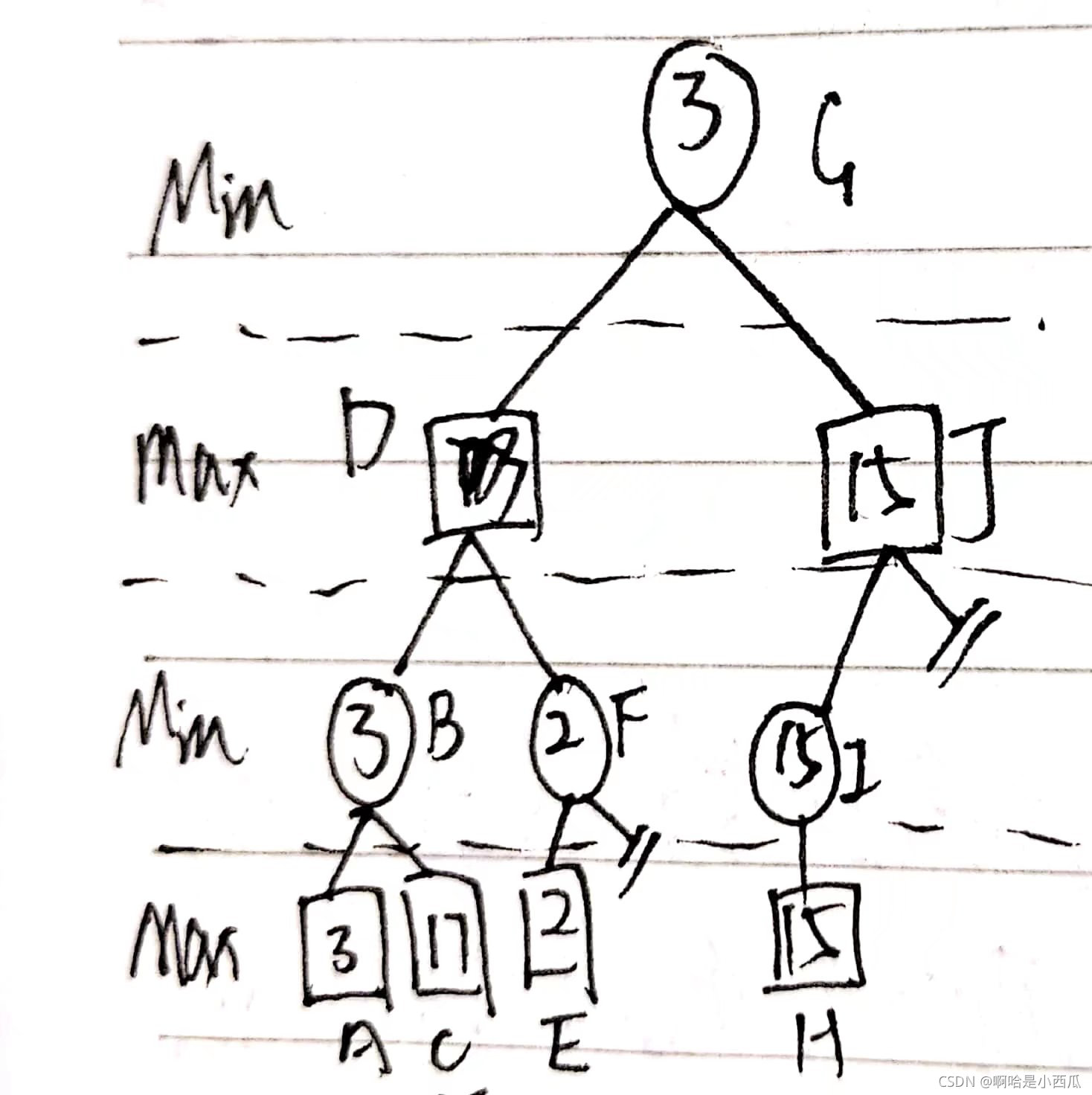
剪枝样例如下图，图中的F进行了Alpha剪枝，J进行了Beta剪枝：

缺陷

1. 极大极小搜索算法和Alpha-Beta剪枝算法很难准确评估胜率，除非将搜索树走到终局。
2. 极大极小搜索算法和Alpha-Beta剪枝算法只适用于搜索小空间。

• 感谢大家的阅读，本文是小编针对极大极小搜索算法和Alpha-Beta算法的学习总结，如理解有误，敬请斧正！