本文主要是介绍[论文理解]旋转等变向量场网络Rotation equivariant vector field networks,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

1. 几个问题
做了什么
提出了旋转等变向量场网络Rotation Equivariant Vector Field Networks (RotEqNet),是一种对旋转等变性(equivariance)、旋转不变性(invariance)和旋转共变性(covariance)进行了编码的CNN网络。
论文中专注于解决“旋转”这一操作,因此下文所述的对象都与旋转有关。
实现原理
每个卷积核被应用在多个方向上,并返回一个矢量场,表示每个空间位置的最高评分方向的大小和角度。
实验效果
相比于一些大型模型,RotEqNet的参数更加紧凑,在图像分类、医学图像分割等任务上能取得和参数更多的模型一样的效果。

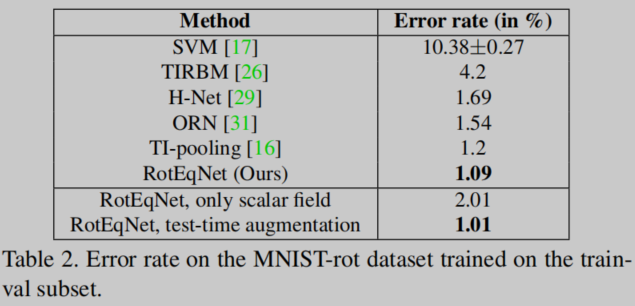
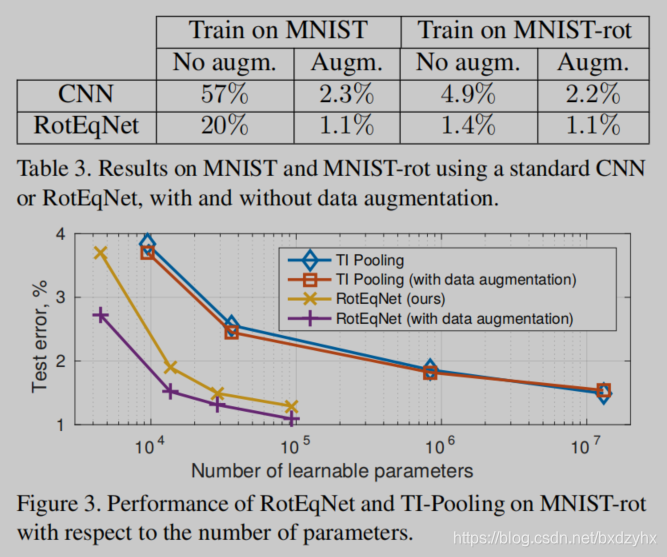
…
实验内容很多,略去不表。
2. 相关工作
有两类方法明确说明了旋转不变性或等变性:
1) 对表示(输入图或特征图)进行转换
2) 对卷积核进行旋转。
RotEqNet属于后者。
2.1 转换image或feature map
- Jaderberg等人提出了Spatial Transformer层,ST也是一个神经网络,会根据输入的图像或特征图预测正确的姿势,然后把输入图或特征图校正到正确的姿势。之前写过一篇关于STN的博客。
- TI-pooling将同一图像的多个旋转版本输入到同一个CNN,然后在第一个全连接层上横跨不同的特征向量执行池操作。这种操作允许紧随其后的全连接层从上一步旋转得到的图像组中挑选出正确的图像,并进行分类。
- Cheng在每一个minibatch中使用了输入图像的几个旋转版本。在第一个全连接层之后,特征图的representation会变得相似,从而迫使CNN学习旋转不变性。
- Henriques对图像进行了扭曲(warp),使卷积固有的平移等方差性质转化为旋转等变性和尺度等变性。
一方面,这些方法具有利用传统CNN实现的优点,因为它们只作用在数据表示(data representation)上。另一方面,他们只能考虑输入图像的全局(global)变换。虽然这非常适合于图像分类等任务,但它限制了它们在其他任务(如语义分割)中的适用性,在这些任务中,某些对象相对于周围环境的局部相对方向才是重要的。相反,RotEqNet是基于特定的CNN构建块来处理本地(local)方位信息。因此,RotEqNet可以处理分类、完全卷积语义分割、检测和回归等多种任务。
2.2 转换filters
3. 数学部分
等变性、不变性和共変性
论文作者用一张图很好地概括了这三者的区别。
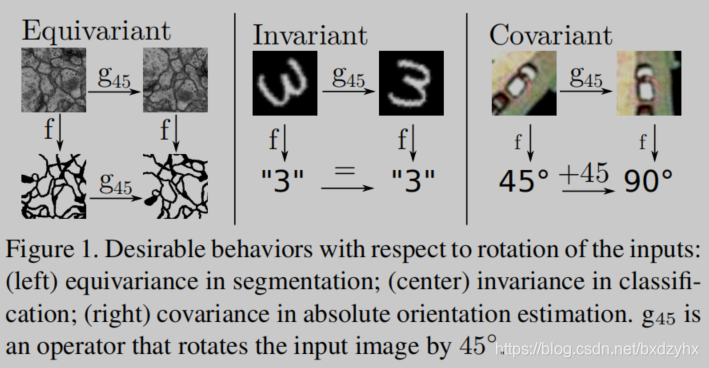
等变性:旋转输入,导致输出被同样地旋转
不变性:旋转输入,输出不变
共变性:旋转输入,输出是输入旋转的确定函数
定义 f f f为某个感兴趣的函数, g g g为某个变换函数。则三种关系可以简单的用公式描述:
等变性: f ( g ( ⋅ ) ) = g ( f ( ⋅ ) ) f\left( {g\left( \cdot \right)} \right) = g\left( {f\left( \cdot \right)} \right) f(g(⋅))=g(f(⋅))
不变性: f ( g ( ⋅ ) ) = f ( ⋅ ) f\left( {g\left( \cdot \right)} \right) = f\left( \cdot \right) f(g(⋅))=f(⋅)
共变性: f ( g ( ⋅ ) ) = g ′ ( f ( ⋅ ) ) f\left( {g\left( \cdot \right)} \right) = g'\left( {f\left( \cdot \right)} \right) f(g(⋅))=g′(f(⋅))
其中 g ′ ( ⋅ ) = h ( g ( ⋅ ) ) g'\left( \cdot \right) = h\left( {g\left( \cdot \right)} \right) g′(⋅)=h(g(⋅)),即 g ′ g' g′是 g g g的函数,是一种二次变换(复合函数)。
在这种定义下,等变性和不变性其实都是共变性的一种特例。
CNN的平移性
图像: x ⃗ ∈ R M × N × d \vec x \in {R^{M \times N \times d}} x∈RM×N×d
卷积核: w ⃗ ∈ R m × n × d \vec w \in {R^{m \times n \times d}} w∈Rm×n×d
图像与卷积核发生卷积: y ⃗ = w ⃗ ∗ x ⃗ \vec y = \vec w*\vec x y=w∗x
RotEqCNN——概述
我们将图片与标准滤波器的若干旋转实例进行卷积,从而获得旋转等变性。
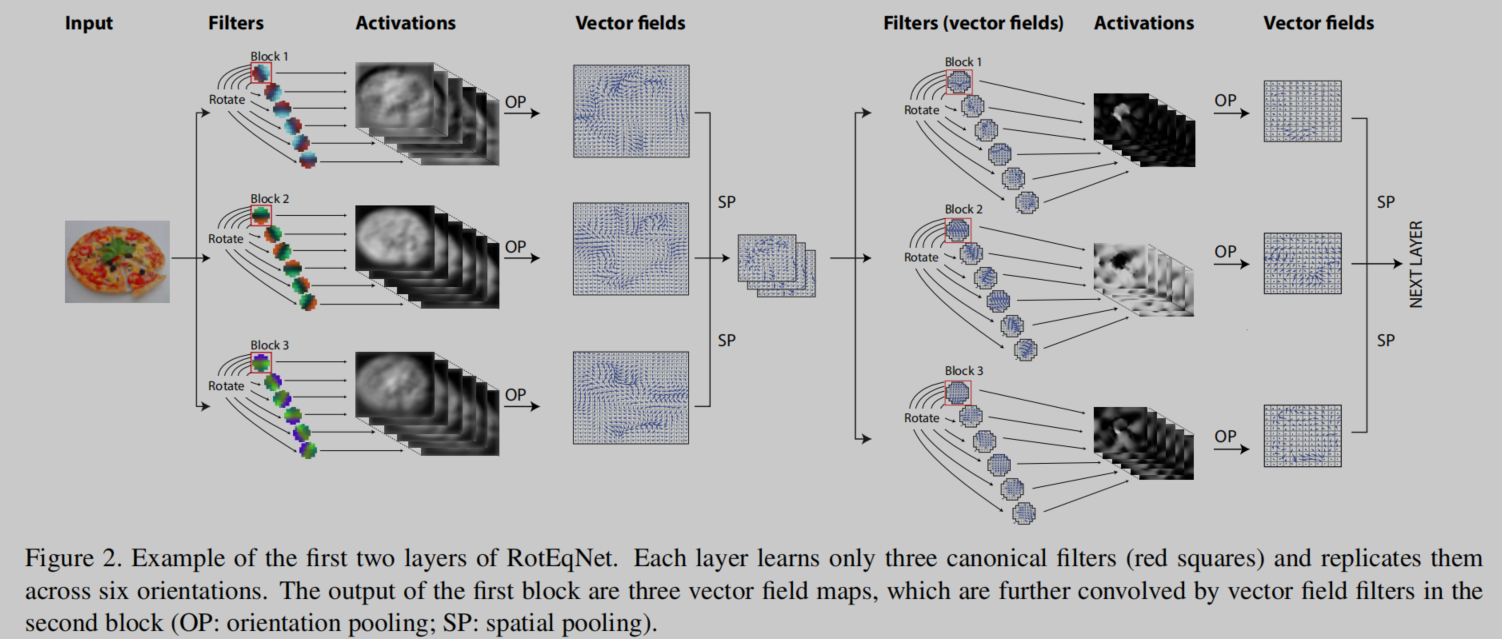
标准卷积核 w → \overrightarrow w w被旋转到 R R R个均匀的空间方向。旋转间隔 α = [ 0 ∘ , 360 ∘ ] \alpha = \left[ {{0^ \circ },{{360}^ \circ }} \right] α=[0∘,360∘],也可以按需调整。卷积核 w → \overrightarrow w w在特定位置的输出包括了所有旋转角度中最大的激活值,以及其对应的角度。如果我们将这个极坐标表示转换到笛卡尔表示,那么每个卷积核 w → \overrightarrow w w会产生一个矢量场特征图 z ∈ R H × W × 2 z \in {R^{H \times W \times 2}} z∈RH×W×2,其中输出的每个位置都包含了两个值 [ u , v ] ∈ R 2 \left[ {u,v} \right] \in {R^2} [u,v]∈R2,对最大激活的大小和方向进行了隐式编码。由于特征映射已经成为向量场,从这一刻起,滤波器也必须是向量场,如图2的右侧所示。用笛卡尔坐标表示z的优点是水平分量和垂直分量[u,v]是正交的,因此可以使用标准卷积在每个分量上独立计算两个向量场的卷积。
RotEqNet的基本单元:RotEqNet block
旋转卷积(RotConv)
给定一个输入图像,并在其周围进行 m / 2 m/2 m/2的零填充,即 x ⃗ ∈ R ( H + m 2 ) × ( W + m 2 ) × d \vec x \in {R^{\left( {H{\rm{ + }}{m \over 2}} \right) \times \left( {W + {m \over 2}} \right) \times d}} x∈R(H+2m)×(W+2m)×d。我们将卷积核 w ⃗ ∈ R m × n × d \vec w \in {R^{m \times n \times d}} w∈Rm×n×d作用在 R R R个方向上。
α r = 360 R r ∀ r = 1 , 2 , . . . , R {\alpha _r} = {{360} \over R}r\;\;\;\forall r = 1,2,...,R αr=R360r∀r=1,2,...,R
每个旋转的 w ⃗ \vec w w是对原有 w ⃗ \vec w w进行中心旋转后的双线性重采样。
w ⃗ r = g α r ( w ⃗ ) {\vec w^r} = {g_{{\alpha _r}}}\left( {\vec w} \right) wr=gαr(w)
其中 g α {g_\alpha } gα代表旋转 α \alpha α度的旋转算符。当旋转不是90°的整数倍时,会需要插值,因此在实际操作中旋转等变性只是近似的。
由于旋转可能会导致卷积核角落附近的权重超出有效的空间范围,因此我们只使用直径为 m m m像素的圆内的权重来计算卷积。也就是说,只采用方形卷积核的“最大内接圆”部分。
输出张量为 y ⃗ ∈ R H × W × R \vec y \in {R^{H \times W \times R}} y∈RH×W×R
y ⃗ ( r ) = ( w ⃗ ∗ x ⃗ r ) ∀ r = 1 , 2 , … , R {\vec y^{\left( r \right)}} = \left( {\vec w*{{\vec x}^r}} \right)\;\;\;\;\forall r = 1,2, \ldots ,R y(r)=(w∗xr)∀r=1,2,…,R
对 x ⃗ \vec x x进行旋转操作,相当于对输出特征图 y ⃗ \vec y y进行了平移。注意,只有标准滤波器 w ⃗ \vec w w被储存在了模型中。在反向传播过程中,相对于每个旋转的卷积核的梯度 ∇ w ⃗ r \nabla {\vec w^r} ∇wr被对齐到标准形式,且进行了求和:
∇ w ⃗ = ∑ r g − α r ( ∇ w ⃗ r ) \nabla \vec w = \sum\limits_r {{g_{ - {\alpha _r}}}\left( {\nabla {{\vec w}^r}} \right)} ∇w=r∑g−αr(∇wr)
这个block可以被用于传统CNN特征映射(如图2的左边)或向量场特征图(图2的右边)。在第二种情况下,卷积是在每个独立分量上单独计算的,最后会生成一个3D的张量:
( z ⃗ ∗ w ⃗ ) = ( z ⃗ u ∗ w ⃗ u ) + ( z ⃗ v ∗ w ⃗ v ) \left( {\vec z*\vec w} \right) = \left( {{{\vec z}_u}*{{\vec w}_u}} \right) + \left( {{{\vec z}_v}*{{\vec w}_v}} \right) (z∗w)=(zu∗wu)+(zv∗wv)
其中 u , v u,v u,v分别代表水平和垂直分量。
当 w ⃗ ∈ R m × m × 2 \vec w \in {R^{m \times m \times 2}} w∈Rm×m×2,即卷积核为2D向量场的时候, g α {g_\alpha } gα也需要被分解,即
w ⃗ u r = cos ( α r ) g α r ( w ⃗ u ) − sin ( α r ) g α r ( w ⃗ v ) \vec w_u^r = \cos \left( {{\alpha _r}} \right){g_{{\alpha _r}}}\left( {{{\vec w}_u}} \right) - \sin \left( {{\alpha _r}} \right){g_{{\alpha _r}}}\left( {{{\vec w}_v}} \right) wur=cos(αr)gαr(wu)−sin(αr)gαr(wv)
w ⃗ v r = cos ( α r ) g α r ( w ⃗ v ) + sin ( α r ) g α r ( w ⃗ u ) \vec w_v^r = \cos \left( {{\alpha _r}} \right){g_{{\alpha _r}}}\left( {{{\vec w}_v}} \right) + \sin \left( {{\alpha _r}} \right){g_{{\alpha _r}}}\left( {{{\vec w}_u}} \right) wvr=cos(αr)gαr(wv)+sin(αr)gαr(wu)
方向池化Orientation pooling (OP)
向量场的Batch normalization
BN将mini-batch中的每个特征映射归一化为零均值和单位标准差。它通过随机梯度下降训练来提高收敛性。
在我们的例子中,由于使用的向量场含有大小和激活的方向两种信息,BN应该只将向量的大小规范化为单位标准差。将角度规范化是没有意义的,因为它们的值已经有界,改变它们的分布会改变有关相对和全局方向的重要信息。给定一个向量场特征映射z及其大小ρ,我们将batch normalization计算为
z ∧ = z v a r ( ρ ) \mathop z\limits^ \wedge = {z \over {\sqrt {{\mathop{\rm var}} \left( \rho \right)} }} z∧=var(ρ)z
计算方面的考量
虽然RotEqNet允许更小的模型,但它们可能需要比标准CNN更多的卷积次数。例如,使用MNIST rot的网络结构,与RotEqNet相比,标准CNN每层需要四倍大小以上的滤波器以达到饱和性能。同时,RotEqNet要求R/4=4.25倍(R=17)个更多的卷积。这使得RotEqNet节省了10倍的模型内存和2倍的数据内存,只需增加1.5倍的计算时间。这是因为,尽管卷积计数更高,但每个卷积的特征映射的数量更小。更少的特征映射意味着更小的卷积滤波器和使用更大的mini-batch的可能性,这两个因素都有助于更快的训练。
局限性
当输入或滤波器上没有主方向时,强制方向池块选择最活跃的方向可能会导致噪声加剧。这是因为任意选择的方向会对输出有很大的影响,以及它将如何与下一层的过滤器交互,但没有任何意义。这个问题通过在滤波器的向量元素和它的输入之间使用标量积来放大,这假设这些向量的方向是相关的。这个问题可以通过在向量元素之间使用自定义的相似性度量来改进,这样就可以考虑到过滤器或输入中的对称性。
4. 模型的工作过程
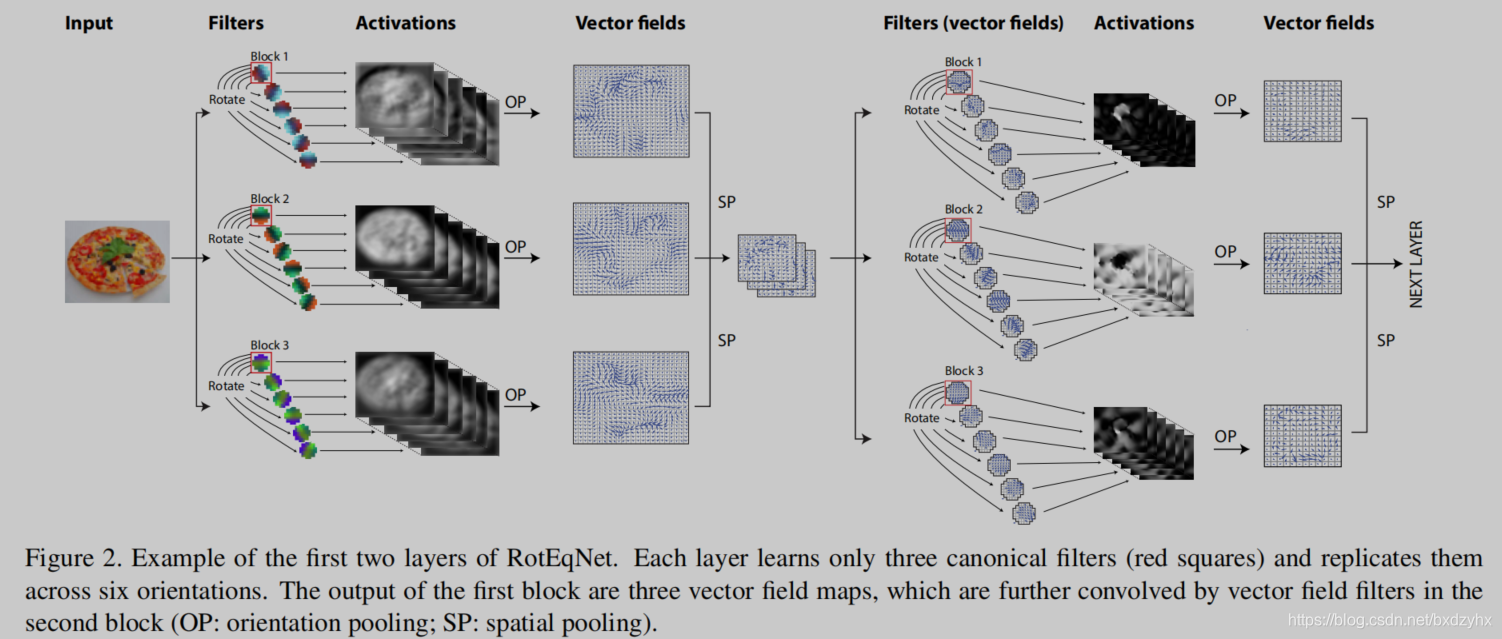
输入一张图,假设有三个filters作用在上面。每个filter都会旋转到若干方向(假设有N个方向),因此总共有 3 × N 3 \times N 3×N张图像。对每组图像(包含 N N N张),想象把他们叠在一起,变成一个 N × W × H N \times W \times H N×W×H的区域,W和H是单张特征图的宽和高。对于 W × H W \times H W×H的区域上的每一个位置,找出 N N N张图中的最大值,并保存为“最大幅度图”,记作 g g g。
g ( x , y ) = max ( f n ( x , y ) ) , n = 1 , 2 , … N g\left( {x,y} \right) = \max \left( {{f_n}\left( {x,y} \right)} \right),n = 1,2, \ldots N g(x,y)=max(fn(x,y)),n=1,2,…N
同样的,由于每个位置的最大值都属于N张图中的一个,而N张图对应旋转的N个角度,因此与 g g g对应的还有"最大角度图" θ ( x , y ) \theta(x,y) θ(x,y)。
输出矢量场假设为 v v v,大小为 W × H W \times H W×H。

总共有3组,就得到了三张矢量图。从N张特征图到1张矢量图的中间过程就是操作OP。
如果输入是矢量图,其实是一样的,不过每个矢量图有两个分量,把两个分量分开处理,最后再组合到一起就好。
有人可能会问,第二次输入有三个矢量图,网络下一步该如何处理?多张矢量图就是不同的channel,可以类比为RGB三色图的三个颜色分量。矢量图数量多了也可以这么想。
这篇关于[论文理解]旋转等变向量场网络Rotation equivariant vector field networks的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






