追踪博弈基础之导引律学习（比例导引、纯跟踪法、差分追踪）

百度百科原译：导引律（ guidance law） 引导飞行器至目的点或与目标相遇的算法。

按照我们常说，导引也可以叫做追踪，引导自身去追踪目标。此处的目标与自身都不限于飞行器，有无人机，无人艇，无人车，机器狗，导弹，飞机，坦克等很多对象。

特别地，导引律不是无人系统的姿态控制和运动控制算法。

1、相对位置

追踪的第一步，知道目标在哪里，有相对位置和全局位置之分。以二维导弹拦截为例。

其中：

r代表了导弹和目标的相对距离，导弹和目标的连线称为目标视线。

q代表了目标视线与攻击平面内某一基准线的夹角，称为目标视线方位角。

V和代表了导弹速度和目标速度。

σ 代表速度和基准线的夹角。

η代表速度和目标视线的夹角，η是导弹前置角，是目标前置角。
追踪的目标是让R为0，即与目标相撞。我们看：

相对距离的变化率等于目标速度和导弹速度在目标视线上分量的代数和

 同时，导弹速度和目标速度的在垂直于目标视线方向上的差值会导致q的变化，

（我们考虑的是从微小变化开始，用到了圆弧公式）

 那么，自寻的制导的相对运动方程组可以表示为：

 其中，ϵ 代表了导引关系式，是一种条件，与导引方法有关，可以反映出各种不同导引弹道的特点。

2、追踪法

思想：导弹的速度矢量始终指向目标，即，导弹前置角始终等于0；

 那么运动方程为：

 其实这种方法，不管从哪个方向发射，导弹总是要绕到目标后面去命中目标，这样会导致导弹弹道较为完全，法向过载较大。并且，追踪法的速度比被严格限制，需要大于1，小于等于2，因此实际应用较少。

3、平行追踪法

思想：在整个导引过程中，目标视线在空间保持平行移动，即相对角度不变。

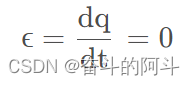
 那么运动方程为：

 优：

当目标直线运动，且目标速度和导弹速度比为常数时，由于平行接近法的性质，η 为常数，因此，导弹的弹道是直线弹道。平行接近法导引的弹道的需用过载小于目标的机动过载
劣：

需要制导系统能够精确测量目标和导弹的速度 以及前置角
由于发射偏差以及干扰的存在，不可能绝对保证导弹的相对速度始终朝向目标，因此平行接近法很难实现。

4、比例导引法

思想：导弹飞行过程中，导弹速度向量V 的转动角速度与目标视线的转动角速度成比例。
 

 其中，K被称为导航比。那么运动方程更新为：

 K的选择：

K 的选择要保证需用过载收敛，此时要求K 要尽可能大，确定了K 的下限。

K 的选择要满足可用过载限制，此时要求K 尽可能小，确定了K 的上限。

K 过大容易引起外接干扰信号被放大。

K 可以是一个常数，也可以时变，通常取在3~6之间。

优：前半段弹道较弯曲，后半段弹道平直，只需要测量和就可以实现导引
劣：命中点导弹需用法向过载受导弹速度和攻击方向的影响

5、纯跟踪算法

思想：将目标的移动轨迹离散化为单个单个的路径点，之后取追逐每个路径点。

这样的话，情况变为顶点追踪问题，只要一次追到各个路径点，我们就完成了对目标的跟踪。

6、差分追击 

差分即将连续时间段划分多个离散时间点，（当然要化分为很多点，间隔要小，因为我们要用圆弧公式）

差分后我们即得到了离散化的运动模型，构建的状态空间如下：

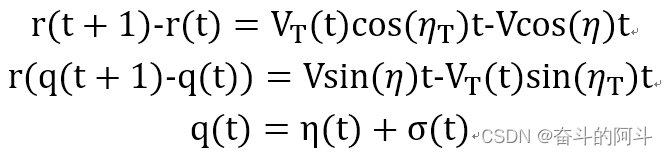
 之后我们可以根据现代控制理论等进一步构建控制律。其涉及内容很多，在此就不过多讲解。具体的例子有反步法、滑模控制等等。

————————————————
本文参考了博主西涯先生的博文，链接如下
原文链接：https://blog.csdn.net/handsome_for_kill/article/details/119476854