补充5 供应链中的需求预测(一)时间序列预测法

        供应链的需求预测方法多样，正如上一篇文章提出的。预测方法分为两部分部分讲，时间序列预测法、基于java的时序预测算法实现及机器学习在预测中的应用。本文为第一部分，介绍时间序列预测法。本文只介绍了几种供应链中常用到的时间序列预测方法，更多预测方法可见金融时间序列分析讲义，讲义虽以金融数据作为讲解，但是预测方法大同小异。

目录

一、静态预测法

 1.估计需求水平和需求趋势

 2.估计季节性因素

 二、适应性预测法

1.移动平均法

2.简单指数平滑法

3.趋势调整的指数平滑法(Holt模型)

4.趋势和季节调整的指数平滑法(Winter模型)

 三、预测误差的度量

---

一、静态预测法

        静态预测法假定，对于系统成分中的需求水平、需求趋势和季节性因素的估计不随观察到的新需求而改变。在这种情况下，利用历史数据来对每一个参数进行估计，然后将估计出的参数值应用于所有的未来预测中。假定需求的系统成分为混合型，也就是说:

系统成分=(需求水平+需求趋势)*季节性因素

        在这里先给出一些基本定义：

        在静态预测法中，在第t期对第t+l期的需求进行预测的计算公式如下：

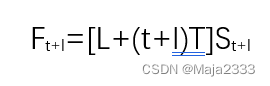
         下面以MoonLight公司的不锈钢为例，进行预测。该公司过去三年的需求数据如下：

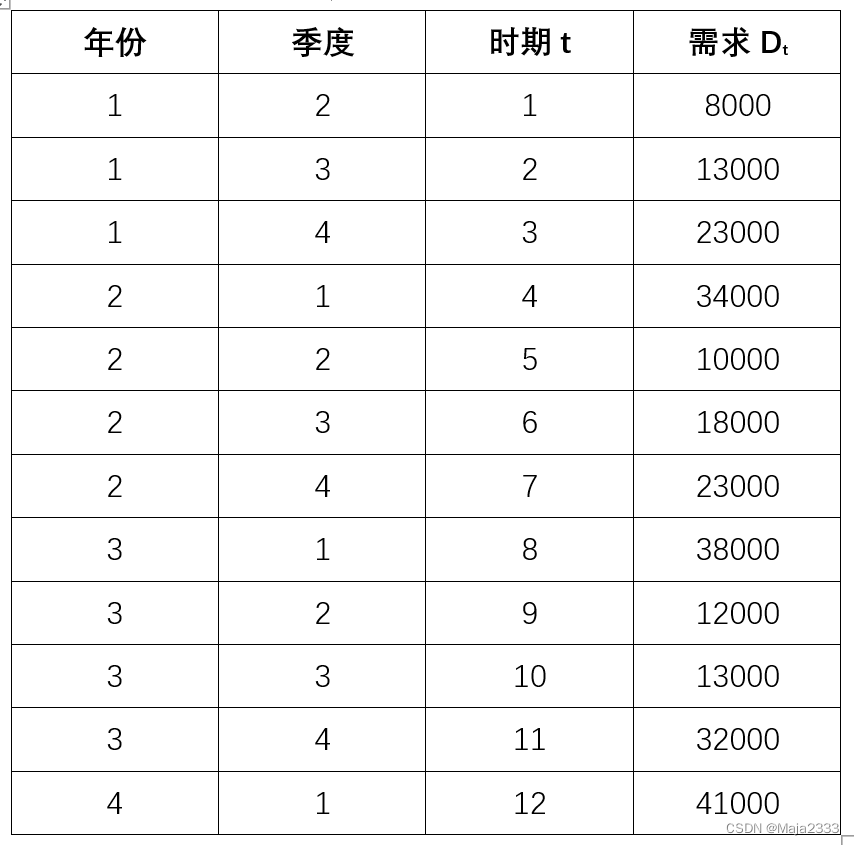
   1.估计需求水平和需求趋势

        首先，需要提出需求数据中的季节性因素。剔除季节性因素的需求(deseason-alized demand) 是指在没有季节性波动的情况下被观察到的需求。时期p(periodicity)是指每次季节性循环包含的期数。在这里p=4。

        第t期剔除季节性因素后的需求可用下面的公式求得：

   

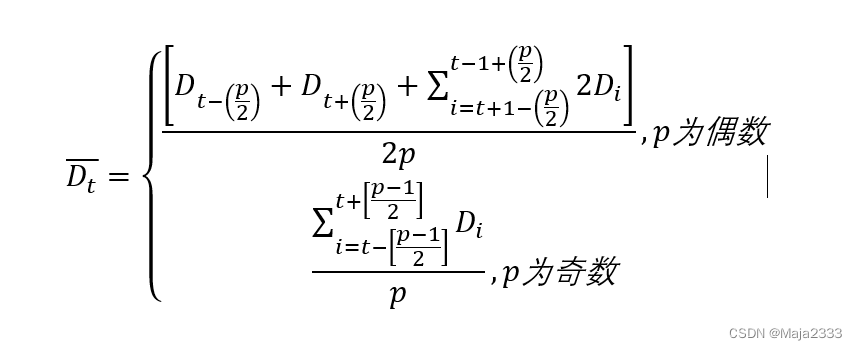
         下面就是上面公司剔除季节性因素后的需求:

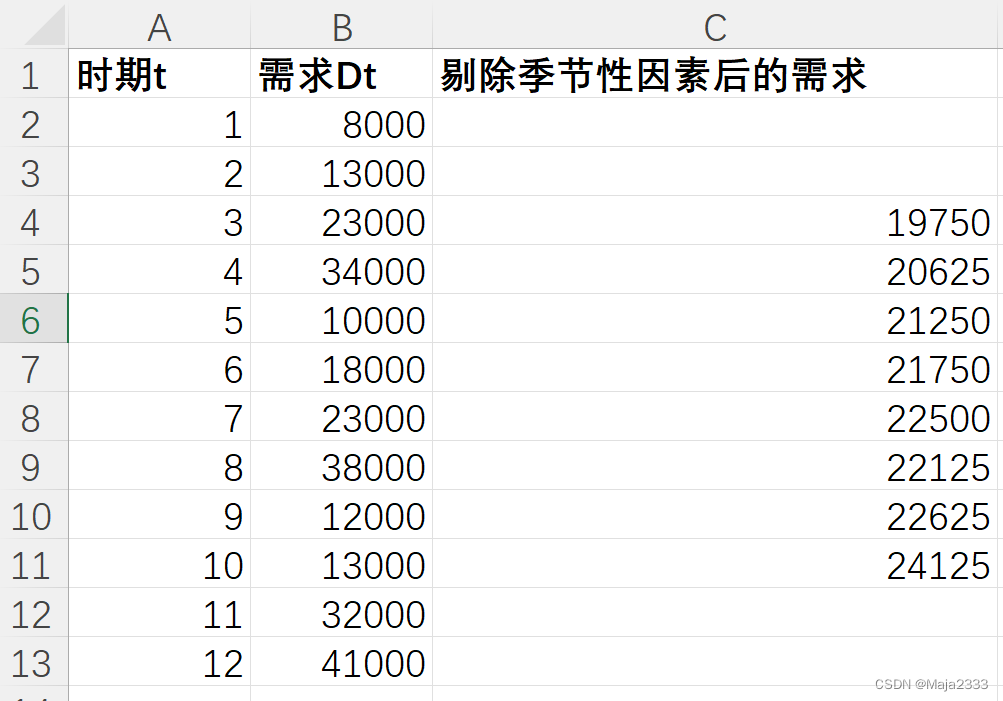
        基于需求随时间的变化，剔除季节性因素后的需求 与时间t质检存在以下线性关系：

        上述的数据，得到的线性关系如下： 

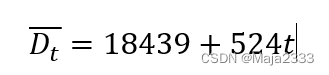
 2.估计季节性因素

        第t期的季节性因素是实际需求Dt和剔除季节性因素后的需求的比值，如下所示：

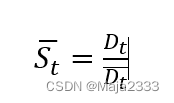
        上面的数据的得到的结果如下所示：         

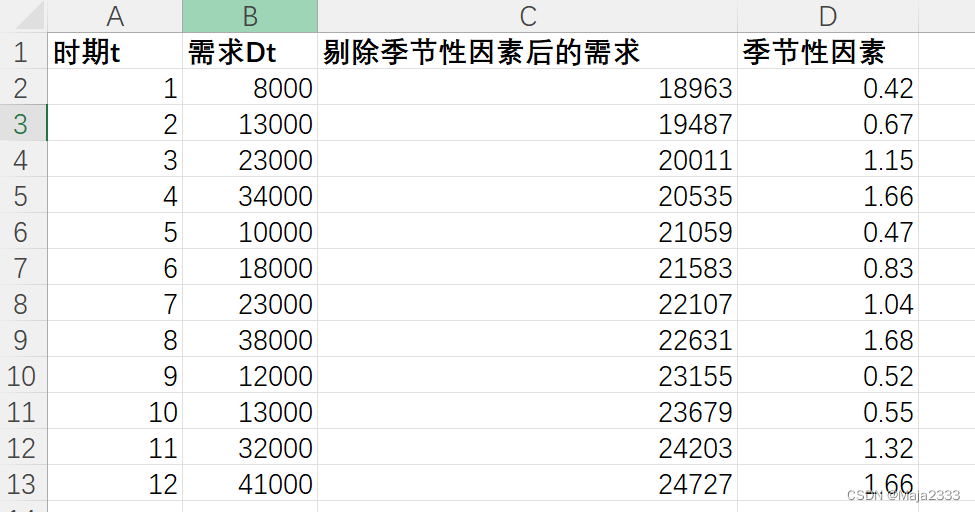
         若在数据中有r个季节性循环，对所有表示形式pt+i(1<=i<=p)的时期，可以计算季节性因素如下：

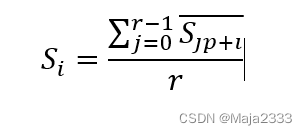
        在这里r=3，季节性因素计算如下： 

        利用静态预测法计算未来4个季度的预测值如下： 

 二、适应性预测法

        在适应性预测中，需求水平、需求趋势和季节性因素的估计值在每次观察到实际需求后都要进行修正。适应性预测法的优点在于估计值中将所有观察到的新数据都考虑其中了。

        首先，先定义下面一些符号：

         在适应性预测法中，利用第t期的需求水平估计值和需求趋势估计值，在第t期对第t+l期进行预测。预测公式如下：

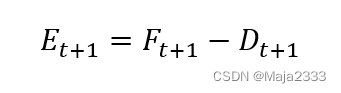
         适应性需求预测框架四个步骤如下：①计算初始值②预测③估计误差④修正估计值

        在预测过程中，选取哪种方法最为合适取决于需求的特性和需求系统成分的组成。在每种情况下，都假定待预测的时期为t。

1.移动平均法

        当需求中没有明显的趋势或季节性因素时，可以用移动平均法进行预测。在这种情况下：

系统的系统成分=需求水平

        在移动平均法中，将最近N个时期需求的平均值作为第t期需求水平的估计值，也就是N期移动平均，具体计算方法如下：

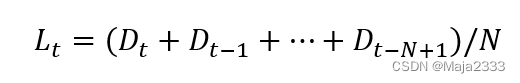
         当前对未来所有时期的预测都是一样，都是基于当前对需求水平的估计。预测公式如下：

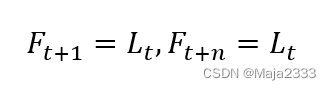
         在观察到第t+1期的实际需求后，我们对估计值进行如下修正：

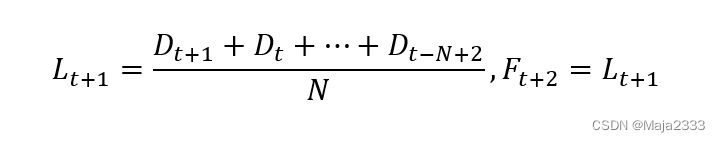
         要计算新的移动平均值，只要加入最新观察值并舍弃最早的观测数据就可以了。修正后的移动平均值则用于对下一期的预测。在进行预测时，移动平均法赋予最近N个时期的数据同样的权重，同时忽略那些较早的数据。当增加移动平均的期数N时，移动平均值对最近观察到的需求响应度会降低。

2.简单指数平滑法

        当需求没有明显的、可观察到的趋势或季节性因素时，采用简单指数平滑法比较合适。在这种情况下：

需求的系统成分=需求水平

        由于假设需求没有明显的趋势或季节性，所以需求水平L0的初始估计值可以用所有数据的平均值来估计。给定从第1期到第n期的需求数据，可以得到：

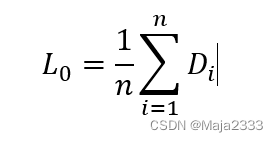
         在第t期对所有未来时期的预测值等于当前的需求水平估计值，可表示如下：

       上式α(0<α<1)为需求水平的平滑系数。修正后的需求水平时观察到的第t+1期的需求(Dt+1)和第t期原来的需求水平估计值(Lt)的加权平均。上式也可改写为

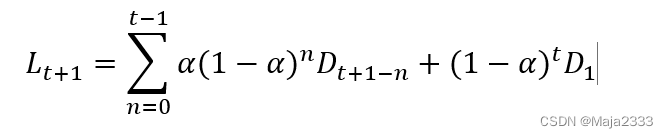
         需求水平的当前估计值时所有历史需求的加权平均，其中近期观察值的权重大，元气观察值的权重小。α取值越大，预测对近期观察值的响应性越好；相反，α取值越小，预测的稳定性越好，但对近期观察值的响应性越差。

3.趋势调整的指数平滑法(Holt模型)

        趋势调整的指数平滑法(Holt模型)适用于需求的系统成分仅包括需求水平和需求趋势，而不存在季节性因素的情况。在这种情况下：

需求的系统成分=需求水平+需求趋势

        通过对需求Dt和时间进行线性回归，可得到需求水平和需求趋势的初始估计值，如下式所示：

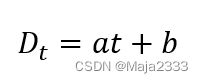
         在这种情况下，由于已经假定需求有趋势成分，但不存在季节性因素，所以对需求和时间进行线性回归是合适的。

        在第t期，给定需求水平估计值Lt和需求趋势估计值Tt，那么未来时期的预测值可表示如下：

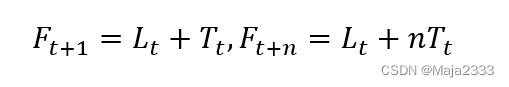
         在观察到第t期的实际需求后，对需求水平和需求趋势的估计值进行如下修正：

   上式α(0<α<1)为需求水平的平滑系数，β(0<β<1)为需求趋势的平滑系数。可以看到，不管是需求水平修正还是需求趋势修正修正后估计值都是实际观察值与原来的估计值的加权平均。

4.趋势和季节调整的指数平滑法(Winter模型)

        Winter模型适用于需求的系统成分中包括需求水平、需求趋势和季节性因素的情况。在这种情况下：

需求的系统成分=(需求水平+需求趋势)*季节性因素

        在第t期，给定需求水平为Lt、需求趋势为Tt和季节性因素为St，...，St+p-1，那么对未来时期的预测可表示为：

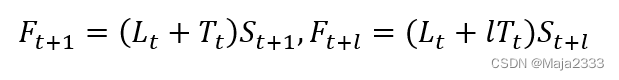
         观察到第t+1期的需求后，对需求水平、需求趋势和季节性因素的估计值进行修正：

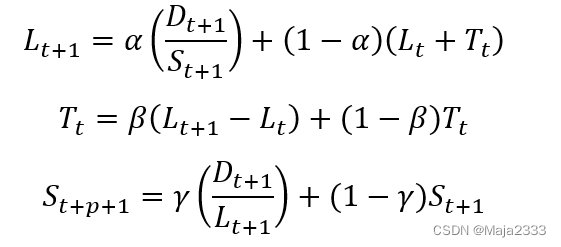
  上式α(0<α<1)为需求水平的平滑系数，β(0<β<1)为需求趋势的平滑系数；γ(0<γ<1)为季节性因素的平滑系数。可以看到，不管是需求水平修正还是需求趋势、季节性因素修正后估计值都是实际观察值与原来的估计值的加权平均。

 三、预测误差的度量

        基于下面两个原因，管理者必须对预测误差进行仔细分析。

        ①管理者可以利用误差分析来判定线性的预测方法是否可以准确预测需求的系统成分。

        ②所有应急计划都必须考虑预测误差。

        只要观察到的误差的历史误差估计范围内，就可以继续使用现行的方法。如果持续超出，就需要及时改变预测方法了。

        第t期的预测误差Et为：

         平均平法误差(MSE)是度量预测误差的常用指标，具体公式如下：

         MSE与预测误差的方差有关，对大误差的惩罚更大。所以，如果较大预测误差引发的成本远大于精确预测带来的收益，则非常适合用MSE这一指标来预测方法进行比较。当预测误差以0为重心对称分布时，也适合用MSE来衡量预测误差。

        平均绝对偏差(MAD)定义为整个预测期内所有时期的绝对偏差的平均值，表达式为：

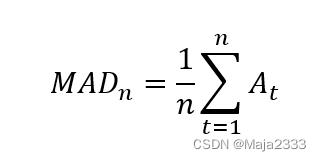
         如果需求的随机成分呈正态分布，那么可用MAD来估计随机成分的标准差，即

σ=1.25MAD

        因此，估计需求的随即成分的均值为0，标准差为σ。在预测误差不是对称分布时，MAD是比MSE更好的误差度量指标。即使是在预测误差对称分布的情况下，如果预测误差的成本和误差的大小成正比，也可以用MAD来选择预测方法。

        平均绝对百分比误差(MAPE)是指绝对偏差站需求的百分比的平均值，计算公式如下：

         当潜在需求具有较强季节性且各期需求变化较大时，MAPE是一个很好的度量预测误差的指标。

        当一种预测方法已不能反应潜在需求模式时(如发生经济危机时)，预测误差不可能以0为中心随机分布。通常，需要一种跟踪和控制预测方法的手段。其中一种手段就是用预测误差的滚动和来评估偏差(bias),公式如下：

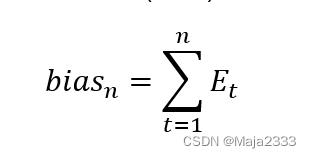
         跟踪信号(TS)是偏差与平均绝对偏差的比值，即

         如果任一时期的TS超出±6的范围外，就说明预测出现了偏差，可能低估了需求(TS<-6)或高估了需求(TS>6)了。之所以出现这种情况，可能是因为预测方法存在缺陷或潜在的需求模式发生了变化。

        当需求突然减少(如发生经济危机时)或急剧增加是的历史数据丧失相关性时，TS也可能增大。如果需求突然减少，那么在进行预测时就要增大当前数据的权重，提高预测的响应性。麦克莱恩建议，在使用指数平滑法进行预测时采用“α值递减”的方法，公式如下：

         长期来看，平滑系数收敛于α=1-β，随着时间的推移，预测值变得更加稳定。