阅读笔记：《Causal Inference for Knowledge Graph based Recommendation》

本文主要是介绍阅读笔记：《Causal Inference for Knowledge Graph based Recommendation》，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

阅读笔记：《Causal Inference for Knowledge Graph based Recommendation》

论文
摘要
背景
方法论
- 问题建模
- 具体方法论
- - backdoor adjustment
  - $f(\cdot),U(\cdot)的实现$
  - 反事实推理策略
  - 损失函数
实验
总结

论文

题目：《Causal Inference for Knowledge Graph based Recommendation》
由Yinwei Wei等人于2022年发表在了IEEE知识与数据工程汇刊，作者目前就职于新加坡国立大学计算机学院，这是第一次尝试通过因果关系来分析和优化基于知识图谱的推荐

摘要

以往的研究通常是将知识图谱作为侧信息，用来补充基于协同过滤的推荐模型，尽管这样做的效果很出色，但是没有做到对基于知识图谱中的属性进行用户偏好建模，主要是因为忽略了以下两点

知识图谱的结构信息可能会阻碍用户偏好的学习
用户的交互属性会导致相似性得分的偏差问题

作者构建了基于知识图谱中变量之间的因果关系，并且确定了导致上述两点出现的原因。并且基于此开发了基于知识图谱的因果推荐（Knowledge Graph-based Causal Recommendation，KGCR）模型。该模型主要有两个创新点，一是在学习用户偏好的时候使用了反混淆技术，二是采用了反事实推理来消除相似性评分的偏差。
最终在Amazon-book,LastFM, Yelp2018三个数据集上进行了广泛实验，证明了其比其他SOTA效果更好。

背景

知识图谱简介：
在这里插入图片描述

作者认为以往的基于知识图谱的推荐都无法对知识图谱中的属性实体的细粒度用户偏好进行建模。在真实的场景中，人们倾向于选择一些特定属性的物品，例如，有人可能会因为导演而观看电影，或者因为品牌而购买鞋子。如下图1所示，用户对通过电影《异形2》互动的Fiction、Michael Biehn和James Cameron属性的偏好严重影响了《时光骇客》和《泰坦尼克号》的推荐。现有的模型，如KGAT和KGIN，似乎可以从她/他的交互属性(用户通过物品交互的属性的简称)中学习细粒度的用户偏好，并对用户和物品表示之间的相似性进行评分。然而，他们面临着以下两个挑战:

知识图谱的结构信息阻碍了用户偏好在属性实体上的表示(通俗易懂的来说，就是知识图谱的结构并不能很好地表示用户更加喜欢哪个属性)。这是因为结构信息决定了哪些属性与物品相关联，以及这些属性(例如，小说，迈克尔·比恩和詹姆斯·卡梅隆)如何与物品(例如，异形II)纠缠在一起。仅仅依靠用户与物品的交互，很难区分用户对这些不同属性的偏好，这不可避免地影响了用户对属性的偏好学习。因此，如何利用用户与物品的交互来了解用户对属性的偏好是面临的第一个挑战。
用户的交互属性会导致相似度得分的偏差问题，可能会在训练阶段提供不准确的监督信号。具体来说，用户交互属性中暴露的属性越多的项目得分越高。在图1所示的同一样本中，迈克尔·比恩(Michael Biehn)饰演的虚构电影《时光骇客》的得分可能高于詹姆斯·卡梅隆(James Cameron)执导的《泰坦尼克号》(Titanic)。因为这些属性为《时光骇客》提供了更多快捷方式(用蓝色曲线表示)，从而绕过了用户对James Cameron的偏好(用红色曲线表示)。因此，如何消除相似性分数的偏差是另一个关键挑战。

作者尝试用因果推断的原理来解释这两种挑战产生的原因。构建了一个因果图来模拟相似性评分的因果因素，如下图2所示：

K：描述用户观察到的item的结构信息
A：用户交互属性
U：基于属性的用户偏好
S：用户-物品对于基于属性的相似度评分
I：以属性为特征的物品表示

在因果图中，K→A说明结构信息决定了用户的交互属性A, K→U反映了用户观察到的属性纠缠。显然，K作为混杂因素，开辟了一条后门路径U←K→A，导致用户偏好与交互属性之间的虚假关系。为了减少其负面影响，作者对因果图进行干预操作，并设计了一个基于知识图的因果推荐(KGCR)模型，该模型实现了反混淆的用户偏好学习，并对用户-物品相似度评分进行建模。（去掉了知识图谱结构的影响，直接考虑用户交互属性对于用户偏好的影响）
对于相似性评分中的偏差问题，作者将其归因于A对S的直接影响。交互属性(A)为预测用户-物品交互提供了一条捷径，绕过了用户对属性U的偏好。因此，我们采用反事实推理来消除A→S造成的偏差。作者估计了事实世界中相似性得分的总效应(total effect, TE)和反事实世界中交互属性对相似性得分的自然直接效应(natural direct effect, NDE)。此后，可以在推理阶段将NDE从TE中移除，以回答以下问题:如果仅根据属性获得用户和项目表示，那么得分S将是多少。（仅考虑基于属性的用户偏好以及物品表示，而不考虑交互属性的情况）

在这里插入图片描述

方法论

关键的定义列出来方便查看：
在这里插入图片描述

问题建模

基于协同过滤的推荐模型： $S_{ui}^{cf} = f_{cf}({\bf{u}}_{cf},{\bf{i}}_{cf}) \tag{1}$
$S_{ui}^{cf}$ 为u与i交互的预测得分，基于协同过滤标志来衡量用户u与物品i交互的可能性，分数函数 $f_{cf}$ 可以用内积或神经网络来实现。
知识图谱表示： $G_{kg} = \{(h,r,t)|h,t \in \varepsilon,r\in R\}\tag{2}$
$\varepsilon$ 是实体的集合， $R$ 是关系的集合，每个三元组描述了从头部实体h到尾部实体t之间的关系r。通过将项目映射到知识图谱的实体中，可以将从知识图谱中学到的外部知识注入到用户和项目的表示中。
基于属性计算的相似性得分： $S_{u,i,a} = f({\bf{u,i}}),where {\bf{u}}=U(O^+_u,G_{kg})\tag{3}$
$S_{u,i,a}$ 是用户与物品的相似度分数， $f (), U ()$ 分别是相似度评分函数和用户偏好建模函数。 $O^+_u$ 是用户u与物品的历史交互集合， $G_{kg}$ 是知识图谱。
本文的任务可以描述为：
输入：用户-物品的历史交互集合和知识图谱
输出：由协同过滤模型计算得到的 $S_{ui}^{cf}$ 和基于属性的相似性得分 $S_{u,i,a}$ 整合得到的用户项目交互预测 $y_{ui}$

具体方法论

backdoor adjustment

在这里插入图片描述
采用了因果推断中常用的反混淆手段，do运算来执行后门调整，来消除K对A的影响，解决挑战1。

K：描述用户观察到的item的结构信息
A：用户交互属性
U：基于属性的用户偏好
S：用户-物品对于基于属性的相似度评分
I：以属性为特征的物品表示

核心理论公式：
$\begin{align*} S_{u,i,a} &= P(S|U={\bf{u}},I={\bf{i}},do(A={\bf{a}})) \\ &= \sum_{k\in K}{P(S|U({\bf{a,k}}),{\bf{i,a}})P({\bf{k}})} \end{align*}\tag{4}$
其中 $P({\bf{k}})=\{P({\bf{k_1}}),\ldots,P({\bf{k_{K'}}}) \}$ 反映了用户观察到的物品与其结构信息相关联的可能性， $U(\cdot)$ 根据用户的交互属性和项的结构信息输出用户偏好的表示
在公式4中，作者强制用户交互属性与所有项目公平交互以实现干预。因此，它能够解开由物品引起的纠缠。因此，有以下公式成立:
$\begin{align*} S_{u,i,a} &= P(S|U={\bf{u}},I={\bf{i}},do(A={\bf{a}})) \\ &= \sum_{k\in K}{P(S|U({\bf{a,k}}),{\bf{i,a}})P({\bf{k}})}\\ &=\sum_{k\in K}f(U({\bf{a,k}}),{\bf{i,a}})P({\bf{k}}) \end{align*}\tag{5}$
其中 $f(\cdot)$ 是对用户和物品之间的相似度进行评分的函数。
在实际情况中，由于样本空间K的大小可能是无限大，依此枚举K中每个值进行计算的成本很高，作者采用计算其归一化加权几何均值(NWGM)来进行近似。得到以下结果：
$\begin{align*} S_{u,i,a} &= P(S|U={\bf{u}},I={\bf{i}},do(A={\bf{a}})) \\ &\approx f(U({\bf{a,\sum_{k\in K}kP({\bf{k}})}}),{\bf{i,a}}) \end{align*}\tag{6}$
它可以近似地将外和 $k\in K$ 带入为表示用户偏好而设计的函数U(·)中，从而减轻计算负担。其中 $f(\cdot),U(\cdot)$ 采用线性函数来实现时，近似误差会最小。

变量 ${\bf{k}}$ 的值由 $\{k_1,\cdots,k_{K'}\}$ 确定，其中每个分量都描述了一个item在属性上的分布。对此，作者将 ${\bf{k}}$ 分解成了两个分量，第一个分量是所有M个项目的分布 $\tilde{k}\in[0,1]^{1\times M}$ ，用来反映哪些item被采样。第二个分量是矩阵 $\in R^{M \times N}$ ，其中每一行描述了对应item在属性上的分布。以图1为例可以表示为 $\tilde{k}=[0,1,0]$ , $K = \{[1,1,0],[1,1,1],[0,0,1]\}$ ，因此公式6可以改写为公式7。这样做了之后，可以改变反事实世界中的分布 $\tilde{k}$ ，以强制公平地暴露于项目的不同结构信息，而不是干扰知识图谱中项目和属性之间的连接。
$\begin{align*} S_{u,i,a} &= P(S|U={\bf{u}},I={\bf{i}},do(A={\bf{a}})) \\ &\approx f(U({\bf{a,\sum_{k\in K}kP({\bf{k}})}}),{\bf{i,a}})\\ &=f(U({\bf{a,\sum_{\tilde{k}\in \tilde{K}}\tilde{k}P({\bf{\tilde{k}}})}}),{\bf{i,a}}) \end{align*}\tag{7}$
同时如果假设每个物品交互的机会均等( $\frac{1}{M}$ )，并且采用同样的方式将 $\bf{a}$ 进行分解为两个分量 $\tilde{a} \in [0,1]^{1\times N}、A\in R^{N \times D}$ ,分别表示交互属性的分布和所有属性表示的矩阵，就有如下公式成立
$\begin{align*} S_{u,i,a} &= P(S|U={\bf{u}},I={\bf{i}},do(A={\bf{a}})) \\ &\approx f(U({\bf{a,E(\tilde{\bf{k}}),K}}),{\bf{i,a}})\\ &=\frac{1}{M}f(U(\bf{a,K}),\bf{i,a})\\ &=\frac{1}{M}f(U(\bf{\tilde{a},A,K}),i,a) \end{align*}\tag{8}$

$f(\cdot),U(\cdot)的实现$

$U(\cdot)的实现$ ：作者提出构造两个二部图用户-属性和项目-属性，并分别对两个二部图进行图卷积运算。
$\bf{p}^{(l+1)} = \sum_{q \in N_p}\frac{1}{\sqrt{|N_p|}\sqrt{|N_q|}}\bf{q}\tag{9}$
其中 $\bf{p}^{(l+1)}$ 是图卷积层(l+1)处第p个节点的表示。 $N_p|、|N_q|$ 分别是节点p和节点q的邻居个数。
通过执行这些操作，将结构信息聚合到属性表示中，然后基于与结构信息关联的交互属性对细粒度用户偏好进行建模。
在这里插入图片描述
$f(\cdot)的实现$ :作者认为相似性得分来自于用户对物品的偏好(即(U, I)→S)和物品与用户交互属性之间的亲和力(即(A, I)→S)。

受到前人的启发，采用乘法融合策略，将分数函数f(·)定义为:
$S_{u,i,a}=f(\bf{u,i,a})=g(\bf(u,i))\sigma(h(\bf{i,a}))\tag{10}$
其中 $\sigma$ 为sigmod函数，另外，g(·)和h(·)是分别对(U, I)→S和(A, I)→S进行建模的函数
为了简单起见，采用内积来实现g(·)
$g(\bf{u,i})=\bf{u\cdot i^{T}}\tag{11}$
h(·)的计算公式：
$S_{i,a} = h(\bf{i,a} = \bf{i\cdot \bar{a}^T}), \bar{a} = \frac{1}{M}\sum_{a\in A}{\bf{a}}\tag{12}$

基于协同信息对用户-物品相似度评分:
$S_{u.i}^{cf}=\bf{u}_{cf}\cdot \bf{i}_{cf}^T$

反事实推理策略

该方案主要是为了解决挑战2，由于A对S的影响造成的是用户-物品相似度评分的偏差问题。采用反事实推理，计算只考虑用户和物品的基于属性的表示而不考虑交互情况下，相似度的得分。

TE：是试验变量(A)对响应变量(S)的因果关系，可以通过当试验变量从reference value变化为excepted value时观测响应变量的变化来估计，在形式上TE的计算公式如下，其中u *和a *为变量u和a的参考值
$S_{u,i,a} - S_{u^*,i,a^*}\tag{13}$
NDE：是在直接路径上仅改变试验变量时响应变量的变化，如图4所示，在形式上NDE的计算公式如下,其中其中(u∗，i, a)是通过对变量u进行do-calculus算子生成的反事实实例，即do(U = u∗)。
$S_{u^*,i,a}-S_{u*,i,a^*}\tag{14}$
在这里插入图片描述
将NDE从TE中剔除，可以得到用户和物品对得分的去偏效应，称为总间接效应(total indirect effect, TIE)。正式地，TIE可表述为如下，其中，由于参考值u *与特定用户无关，因此 $s_i$ 可以由g(u, i)的输出的平均值来计算。
$\begin{aligned}T I E & =T E-N D E \\& =S_{u, i, a}-S_{u^{*}, i, a^{*}}-S_{u^{*}, i, a}+S_{u^{*}, i, a^{*}} \\& =g(\mathbf{u}, \mathbf{i}) \sigma(h(\mathbf{i}, \mathbf{a}))-g\left(\mathbf{u}^{*}, \mathbf{i}\right) \sigma(h(\mathbf{i}, \mathbf{a})) \\& =\left(g(\mathbf{u}, \mathbf{i})-s_{i}\right) \sigma(h(\mathbf{i}, \mathbf{a})) .\end{aligned}\tag{15}$

最后，我们将去偏见相似度得分与协作得分结合起来预测用户与物品之间的交互，预测分数形式上为：
$y_{ui}=S_{ui}^{cf}+S_{ui}^{kg} = \bf{u}_{cf}\cdot \bf{i}_{cf}^T + \left(g(\mathbf{u}, \mathbf{i})-s_{i}\right) \sigma(h(\mathbf{i}, \mathbf{a}))\tag{16}$

损失函数

在这里插入图片描述
作者采用的是BPR loss，总的损失函数为：
$\mathcal{L}=\mathcal{L}_{1}+\alpha \mathcal{L}_{2}+\|\Theta\|_{2}$
其中 $\alpha$ 是用来平衡两个损失函数的超参， $\|\Theta\|_{2}$ 是正则项
$\mathcal{L}_{1}$ 公式如下：
$\mathcal{L}_{1}=\sum_{(u, i, j) \in \mathcal{O}}-\ln \sigma\left(S_{u, i, a}+S_{u, i}^{c f}-S_{u, j, a}-S_{u, j}^{c f}\right)\tag{17}$
其中 $\mathcal{O} = \{(u,i,j)|(u,i) \in \mathcal{O}^+,(u,i) \in \mathcal{O}^-\}$ ,+，-分别表示观察到的和未观察到的用户-项目对组成的训练集。

$\mathcal{L}_{2}$ 公式如下，同时用来监督h()的输出：
$\mathcal{L}_{2}=\sum_{(u, i, j) \in \mathcal{O}} \max \left(0, \sigma\left(S_{i, a}\right)-\sigma\left(S_{j, a}\right)-m\right)\tag{18}$
其中m是预先定义的阈值，用来控制正负对预测值之间的差值。

实验

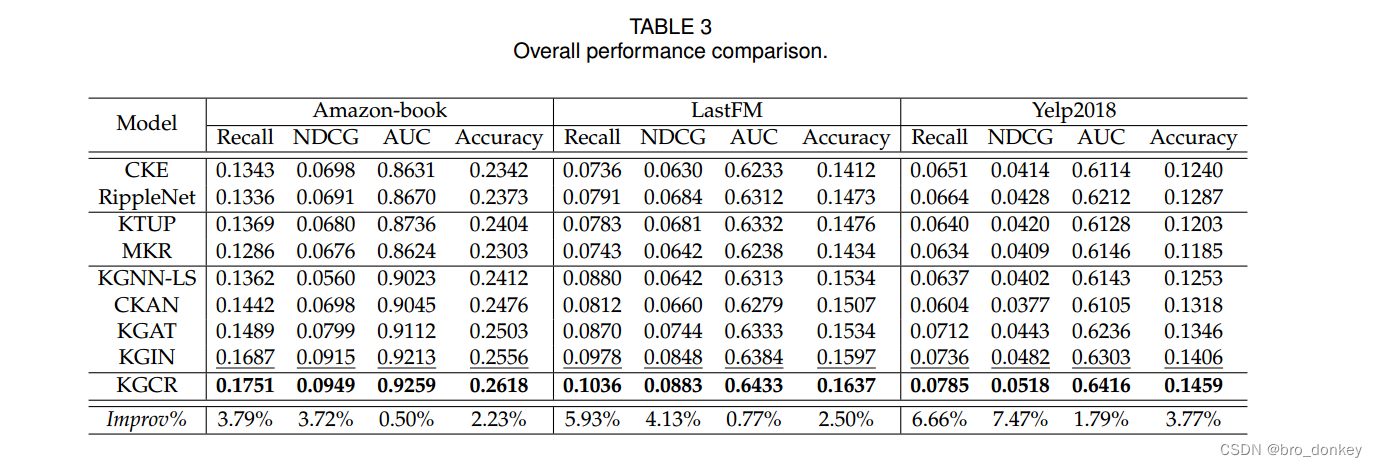
作者还进行了消融实验，感兴趣的可以自行查看

总结

这是因果推断在基于知识图谱推荐的初次应用，其实无论是反混淆技术还是反事实技术在因果推断中都是非常常见的技术。我觉得本文的新颖的点是在于如何运用这些技术，如何建模，如何讲好故事。最新颖的点应当就是下列这幅图，作者讲好了自己的故事，构建了这样的因果关系图，之后再用因果推断技术去解决。
整体的模型架构值得借鉴，只不过关于因果关系图的各个变量解释我认为没有太清楚，如果能够再举一个详细的例子解释一下，可能文章理解的效果会更好。

在这里插入图片描述

这篇关于阅读笔记：《Causal Inference for Knowledge Graph based Recommendation》的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！