基于 FPGA 的相控阵天线波束控制器设计

摘 要:相控阵天线的电扫描特性使其具有扫描灵活、指向精确、可靠性高和抗干扰能力强等特点。 波束控制 技术作为相控阵天线的关键技术之一,直接影响系统效能的发挥。 多波束相控阵天线支持跳波束通信模式,对波束 的快速切换提出了更高的要求。 针对波束扫描快速响应需求,对常规波束控制算法进行分解和优化,提出了一种基 于现场可编程门阵列(FPGA)的移相码快速计算方法,采用 cordic IP 核计算公共因子三角函数值、乘法器 IP 核做有 符号小数乘法运算、查表赋值法进行小数乘加运算、分区比较法对数据进行归一化处理和除法计算,每个单元移相 码计算时间仅 3 个时钟周期。 满阵 256 单元计算时间约 26 us,通过仿真表明,该算法可以快速而准确的计算出天 线单元所需的移相码,实现波束扫描快速响应性能。

关键词:相控阵天线;波束控制;cordic;FPGA

引言

相控阵天线是由许多辐射单元排成阵列形式构 成的天线,利用计算及控制移相器改变天线孔径上 的相位分布来实现波束在空间扫描[1] ,具有无物理 运动的转向、高的二维扫描灵活性以及极准确的波 束指向、可靠性高、抗干扰能力强等特点[2] 。 相控阵 技术目前已广泛应用于搜索、火控、制导等各种战术 雷达和着陆、气象等民用雷达、通信卫星、电子对抗 等领域[3-5] 。 在相控阵天线中,波束控制技术作为关键技术 之一,直接影响系统效能的发挥[6] ,尤其是支持跳波 束多区域时分通信模式[7] 的多波束相控阵天线,一 次波束驻留时间最小 50 us, 即要求波束控制器 在 50 us 内完成 256 单元移相码计算和将移相码送 到对应的移相器上。 波束控制器性能好坏直接影响 整个相控阵系统的整体性能和技术指标。 256 单元阵面规模决定了移相码计算方法需使 用集中式运算法。 集中式运算法多采用查表预处理 法和软件计算法[8] 。 查表法将每个波位下所有移相 码存于存储器中,工作时通过查表方式得到移相 码[9] 。 由于资源需求较大,存储器需选用大容量 NAND FLASH 作 为 外 部 存 储 器[10] 。 可 选 用 的 NAND FLASH 在读取数据时等待时间一般为 25 us30 us,甚至更高。 将移相码送到对应移相器上需要 20 us 时间。 在 50 us 内可用于从外部存储器读取数 据的时间很短,甚至没有读取数据时间。 软件计算 法由 DSP 或单片机等计算移相码,然后传送至 FPGA,FPGA 将移相码送到对应的移相器。 以运算速 度较快的 DSP 为例,DSP 计算 256 单元移相码时间 需要 10 ms 左右(频率 120 MHz),仅计算时间就是 波束驻留时间的 200 倍。 本文针对移相码快速计算问题,提出了一种基 于 FPGA 的实时计算方法[11] ,该方法通过对算法进 行分解和优化,只需要 3 个时钟周期即可计算出一 个单元的移相码,满阵 256 单元计算时间约为 26 us (时钟 30 MHz)。 仿真结果表明,该方法计算速度 快,实现了波束扫描快速响应性能。

1 、相控阵天线原理及算法

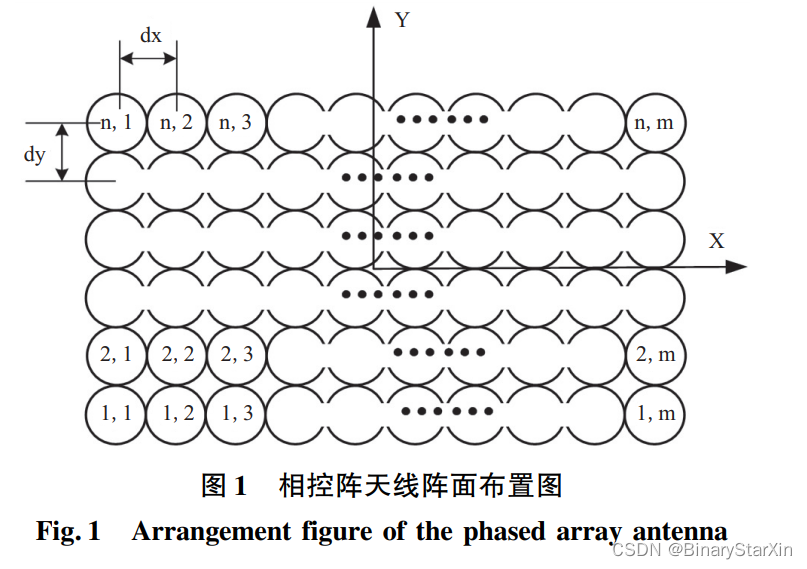
相控阵天线是由大量的辐射单元组成的阵列 (正方形、三角形、稀疏矩阵等),辐射单元几百、几 千,甚至上万[12] ,辐射单元由数字移相器控制,工作时通过根据指向角度计算并配置相应的移相码,达 到控制天线指向的目的[13] 。 如图 1 所示,设定天线共有 m∗n 个天线单元, 单元间距分别为 dx 和 dy,λ 为波长,θ 和 φ 分别为 对应目标的俯仰角和方位角,m 代表列,n 代表行。

 

计算结果与初始校正值累加,得到最终的移相 码。 移相码计算有 sinθ、cosφ、sinφ 正余弦求解、有 小数加减法和乘除法计算、归一化处理,算法比较复 杂。 对于不同的方位角、俯仰角,计算出辐射单元移 相码,并将移相码送到移相器中,才能保证相控阵雷 达的灵活性和多样性,快速准确计算移相码是波束 控制器的难点。

2、 波束控制器系统设计

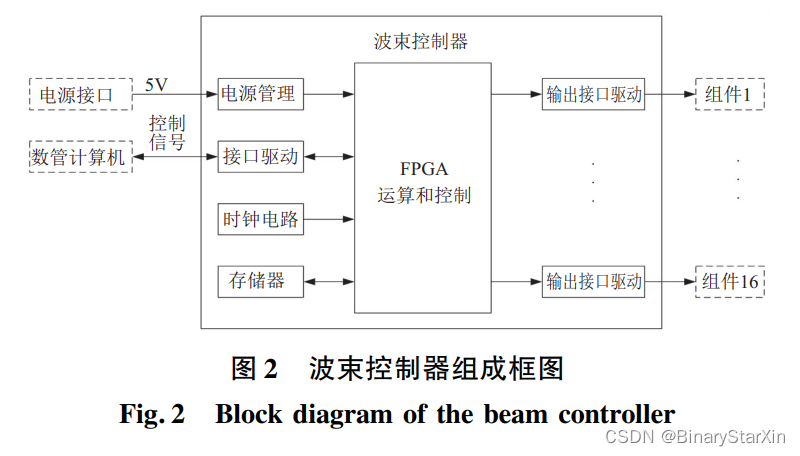
为了快速而准确计算移相码,设计了以 FPGA 为核心的波束控制器,FPGA 进行算法运算和时序 控制[14] ,省去 DSP 处理芯片,简化了硬件电路设计。 组成框图如图 2 所示 ：

波束控制器从数管计算机通过 RS422 串口接收 到控制命令后,根据输入角度计算出相对应的移相 码,同时从外部存储器中读出相位校正值,将两者相 加并发送给移相器,移相器在控制信号的作用下,偏 移到指定相位,从而达到改变波束的目的。 波束控制器硬件电路主要包括 FPGA、电源管 理、接口驱动电路、存储器、时钟电路。 各部分电路 作用如下:

1)FPGA 为核心器件,负责接收并解析数管计 算机发送的控制指令、管理外部存储器单元、计算移 相码、给组件发送移相码等控制指令;

2)接口驱动电路实现信号的电平转换和隔离;

3)时钟电路为 FPGA 提供所需时钟信号; 4)存储器中存储相控阵天线初始相位校正值。 

3 、FPGA 算法实现

3. 1 软件算法流程

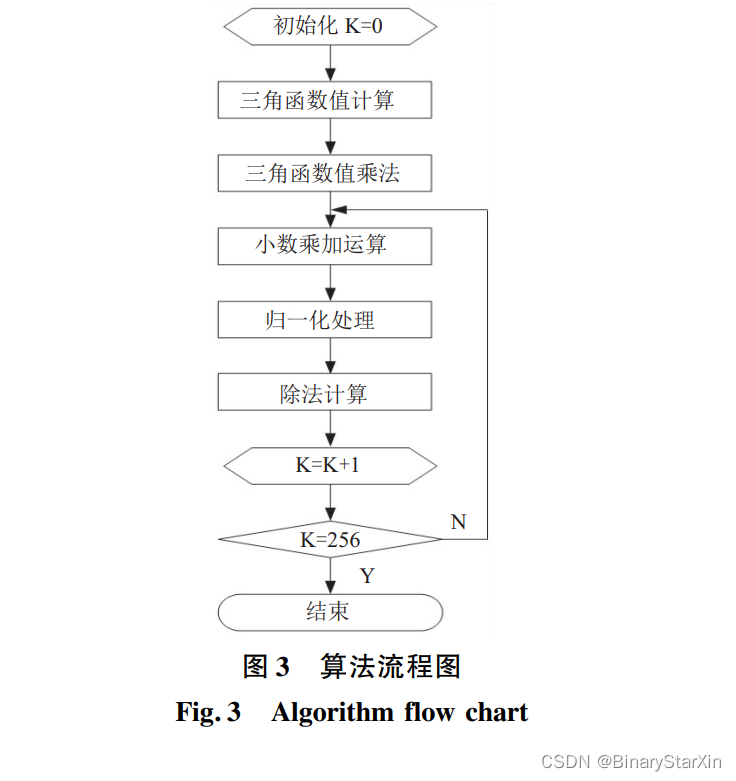
为满足快速计算需求,本设计对算法进行分解 优化,采取面积换速度的思想,每一步设计都采用时 间需求最小的设计方法,计算流程图如图 3 所示。 首先,需要求解出公共因子三角函数值,并进行三角 函数值乘法运算。 本设计采用 cordic IP 核计算三角 函数值[15] ,需要 1 个时钟周期,然后对数据进行锁 存,需要 1 个时钟周期,三角函数乘法运算需要 1 个 时钟周期,共 3 个时钟周期。 完成三角函数值乘法 运算后,需要分别计算每个单元的移相码,该计算过 程包含 3 个步骤,分别是小数乘加运算、归一化处理 和除法计算,每个步骤只需要 1 个时钟周期即可完 成。 因此,仅需要 3 个时钟周期即可完成一个单元 的移相码计算。 根据本设计方案,全部的计算过程共计需要 3 个时钟周期完成公共因子三角函数值计算和三角函数值乘法运算,需要 256 × 3 个时钟周期完成全部 256 个单元的移相码计算,总计需要 3+256×3 = 771 个时钟周期。 在本设计中采用 30 MHz 系统时钟, 771 个时钟周期所占时间为 771÷30 = 25. 7 us。 计算流程图如下:

(1)三角函数值计算 当 FPGA 接收到指向角输入时,先进行指向角 的三角函数 运 算。 三 角 函 数 运 算 采 用 FPGA 的 cordic IP 核进行计算,1 个时钟周期就可得出三角函 数值。

(2)三角函数值乘法 得到三角函数值后,进行 sinθ 与 cosφ,sinθ 与 sinφ 乘积运算。 采用乘法器核进行有符号小数乘法 运算。

(3)小数乘加运算 接下来按照公式(1) 进行移相码计算,公式可 拆分成 ：

个数据乘除法,用 FPGA 实时计算起来要耗费多个 乘法器资源和多个时钟周期,本设计采用查表赋值 方法,事先计算出 256 单元的 360 λ dx(m - 8. 5) 、 360 λ dy(n - 8. 5) 值,存储在 FPGA 中,在计算时,三 角函数乘积作为乘法器的一个输入端,将事先计算好 的系数作为乘法器的另一个输入赋给乘法器,这样每 计算一次进行一次系数赋值,仅需 2 个乘法器、一个 加法器和 1 个时钟周期即可得出所需要的数据。

(4)归一化处理 计算的结果要归一化到 0-360 之间。 如计算结 果为正数,与 360 比较,大于 360,则减去 360,继续 与 360 进行比较,直到数据在 0-360 之间;如计算结 果为负数,则加上 360,比较数据是否在 0-360 之间, 不在,则继续加 360,直到数据在 0-360 之间。 采取 传统的比较、加减循环操作,将数据归一化到 0-360 之间,每次数据归一化时间不定。 如遇到一个很大 的数,要多个时钟周期才能完成归一化。 例如计算 结果为 3500,则需要 9 次比较和减法才能完成数据 归一化。 按平均 1 个数据 9 个周期计算,系统时钟 30 MHz,仅归一化 256 个数据就需要 76. 7 us。 为避 免多次比较和加减运算,本设计采用分区比较方法, 以 360 为一个区间大小,以 360 的整数倍值作为区 间边界,划分多个数据区间,数据分区包含所有可能 计算出来的数据。 将计算出来的数据与数据分区边 界值进行比较,如果计算出来的数据为负值,加上左 边界值的绝对值;如果为正值,则减去左边界值,加 或减后的数据就在 0-360 之间。 与数据分区左边界 值绝对值相加或左边界值相减,相当于进行了多次 比较和加减,所以无论数据多大,都只需要 1 次比较 和加减即可完成归一化处理。 例如对于特定的天 线,公式(1)中的参数都是已知的,根据这些参数可 以估算出由公式(1) 计算的结果最大值和最小值。 假设估算出最大值为 5330,最小值为-5330。 我们 将数据分成[ -5400,-5040)、[ -5040,-4680)、…、 [-3600, - 3240)、 … [ - 360,0)、 [0,360)、 [360, 720)、…、[3240,3600)、…、[4680,5040) 、[5040, 5400]等数据分区,这些数据区间大小都是 360,区 间边界值是 360 的 - 15、 - 14、 - 13、 …、 - 10、 - 9、 …、-1、0、1、2、…、9、10、…、13、14、15 倍。 同样计算 结 果 是 3500, 将 3500 与 区 间 边 界 - 5400、 - 5040、-4680、…、3240、3600、…、4680、5040、5400 等 比较,3500 大于 3240, 小于 3600, 3500 在 [ 3240, 3600)数据区间内,3500 为正值,用 3500 减去数据 区间的左边界值 3240,就相当于做了 9 次与 360 的 比较和减法,比较和减法在 FPGA 内只需要 1 个时 钟周期就能实现,即 1 个时钟周期得出归一化结果 为 260。 同样系统时钟30MHz,归一化256 个数据只 需要 8. 533 us。

(5)除法计算除法计算是归一化的数据除以相 移 5. 625,然后四舍五入得出相位数据,传统的移位 比较减方法,算出一个数据需要多个时钟周期。 本 设计依然采用分区比较的方法,将归一化的数据与 事先计算好的数据区间进行比较,一个时钟周期即 可得出移相码。 如计算结果为 260,比较数据在 261. 5625 与 267. 1875 之间,得出移相码为 101111。 为方便运算和保证精度需求,本设计中小数运 算采用扩大为整数的方式[16] ,扩大倍数取决于所需 要的计算精度。 3. 2 仿真结果

MATLAB 计算值如图 4 所示,其中 Theta 为 8 度 俯仰角,Phi 为 44. 8 度方位角,Freq 为 29. 7 GHz 频 率,A 为输出的移相码。

ISE 软件仿真结果如图 5 所示,激励文件中 phase_inthe 代表 theta,phase_inphi 代表 phi,单位均 为弧度。 输入角度采用 16 位表示,为定点补码 2QN 格式,0X0478 转换成二进制“0000010001111000”, 按照 IP 核定义相当于 000. 0010001111000,小数后 第三位为 1,代表 2 -3 ,以此类推,所有为 1 的位代表 的值之和,就是所表示的值,即 2 -3 +2 -7 +2 -8 +2 -9 + 2 -10 之和为 0. 1396484375 弧度,转换成角度是 8 度, 同理 0X1900 转换成角度是 44. 8 度。 29. 7GHz 频率 体现在查找表里。 通过图 4 和图 5 进行比较,FPGA 计算出来的值与 MATLAB 计算出来的值是相同的。 由此可见,此方案计算出了正确的移相码。 从图 5 中可以看出,在复位后,经过 3 个时钟周期的三角函 数求解和乘积运算后,再经过 3 个时钟周期计算,共计 6 个周期后得出第一个移相码 54。 其后每经过 3 个周期,依次计算出移相码 63、7、15、24 等,每个移 相码计算周期仅需要 3 个时钟周期,完全满足快速 计算需求。

4 、结束语

波束扫描响应时间是相控阵天线的重要性能指 标,相控阵各种先进的工作方式对波束扫描的响应 时间提出了越来越高的要求。 采用本方案设计的波 束控制器,硬件电路简单,软件上对算法进行分解和 优化,计算一个单元移相码只需要 3 个时钟周期,满 阵 256 单元移相码计算时间缩短至 26 us(时钟 30 MHz),具有非常短的波束响应时间,提高了波束扫 描的速度和灵活性。