脉冲法和方向盘转角法计算车辆位置不同应用工况

1. 脉冲法计算车辆位置

在定义下的世界坐标系中，车辆运动分为右转后退、右转前进、左转后退、左转前进、直线前进、直线后退和静止七种工况，因此需要推倒出一组包含脉冲、车辆运动方向和车辆结构尺寸参数的综合方程式进行车辆轨迹的实时迭代计算。由于直线行驶和曲线行驶的半径分别是无穷大和正常值，因此分为直线行驶和曲线行驶两种工况。在以下公式推导中，所有弧长和弦长微元值无符号，而车辆偏航角微元值带正负。

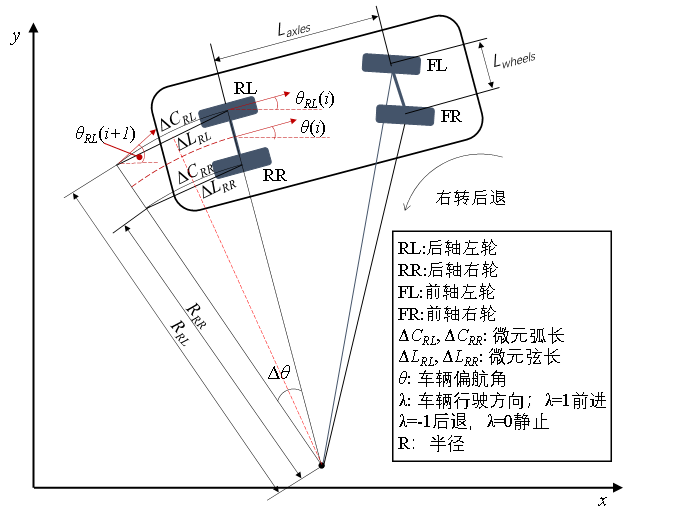
图1 车辆阿克曼转向运动图

1.1 直线行驶

直线行驶的判断依据是:

后轴右车轮的坐标偏航角为：

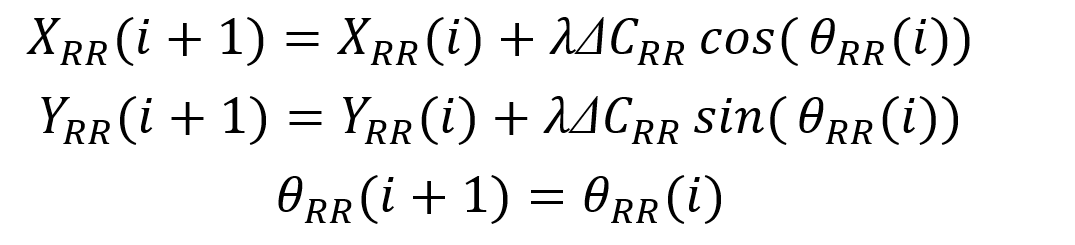
后轴左车轮的坐标偏航角为：

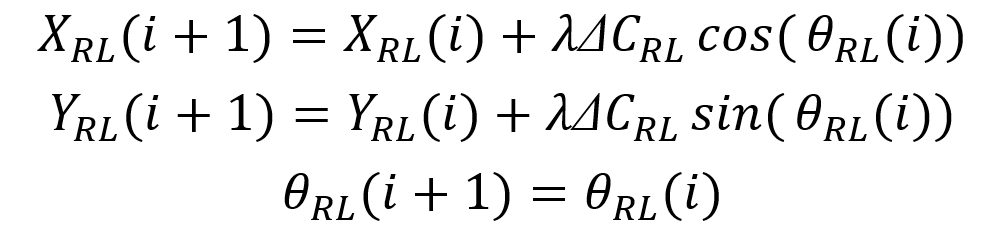
因此后轴中心的坐标偏航角为：

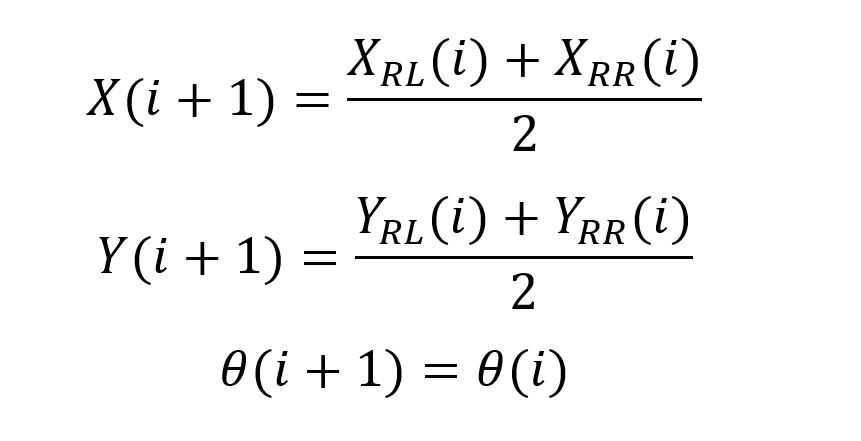
1.2 曲线行驶

曲线行驶的判断依据是：

当车辆转向时，车辆绕瞬时转动中心进行旋转；对于低速泊车，忽略车辆柔性体轮胎侧偏特性导致的车辆瞬时转动中心与后轴延长线不重合特性。假设车辆旋转运动为纯刚体运动，则采样周期内后轴车轮的脉冲差值满足以下关系：

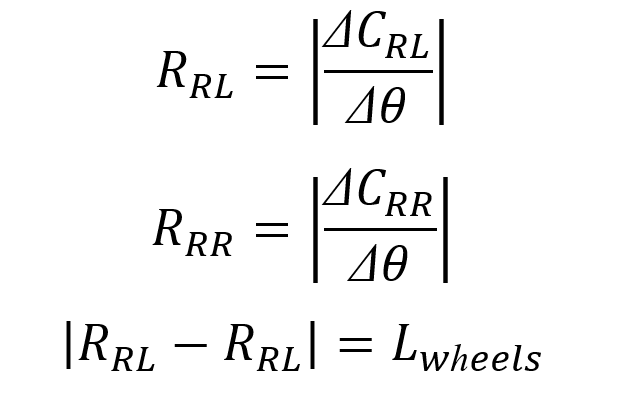
在这里可以看出，公式包含半径参数，由于半径参数会出现较大的计算误差，联立方程组可以减少计算误差；考虑到车辆偏航角变化情况由车辆运动方向和转动方向决定，综合上式可得偏航角变化量为：

可以看出，该公式不涉及半径参数，只包含脉冲差值、车辆轮距和行驶方向，大量实验验证，可以保证较高的偏航角计算精度；车辆后退右转偏航角增大，车辆后退左转偏航角减少，车辆前进右转偏航角减小，车辆前进左转偏航角增大。另外，如图2所示，可以看出当车辆沿着单方向行驶时，车辆初始的偏航角仅与起点和终点车轮脉冲有关。

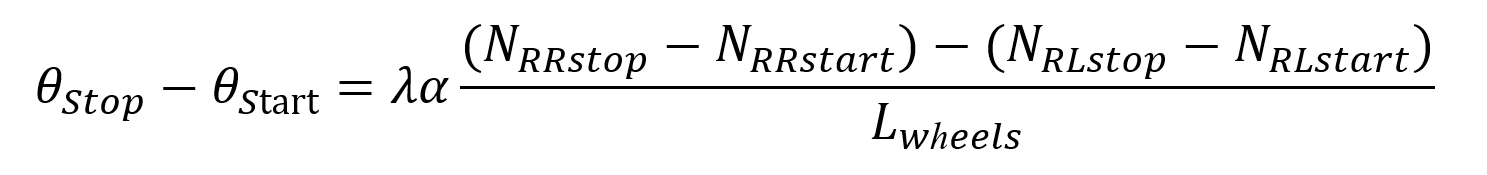
这里N-车轮脉冲个数，α-单个脉冲车轮滚动距离，需标定。

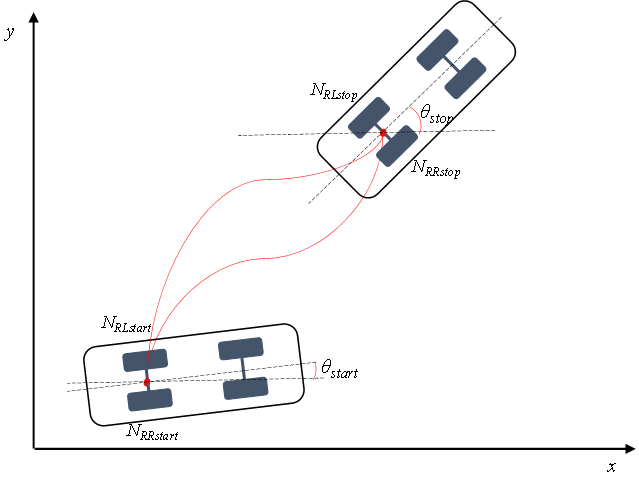
图2 车辆单方向行驶不同路径起点终点位置图

根据图1，后轴右车轮的坐标偏航角为：

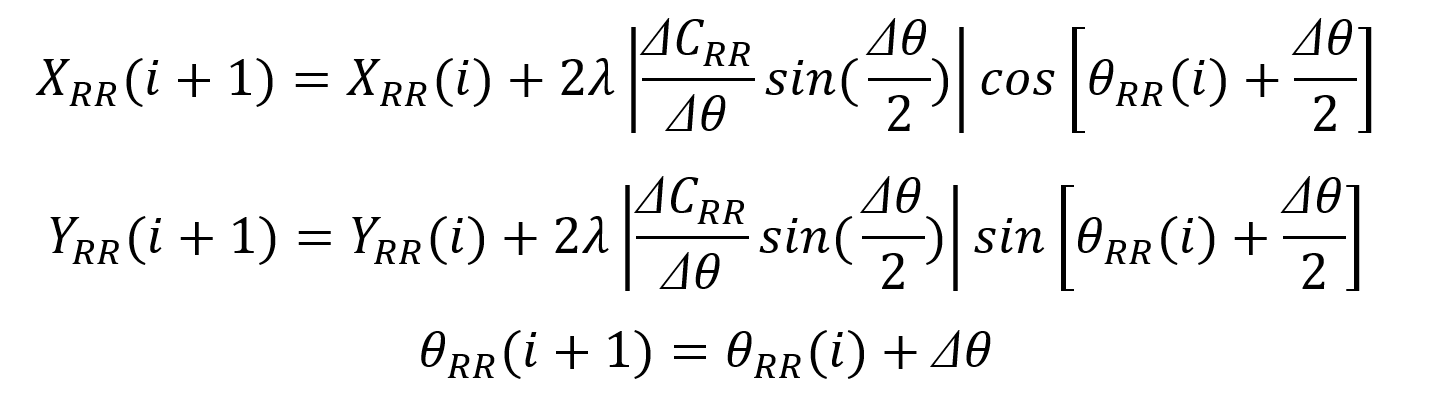
后轴左车轮的坐标偏航角为：

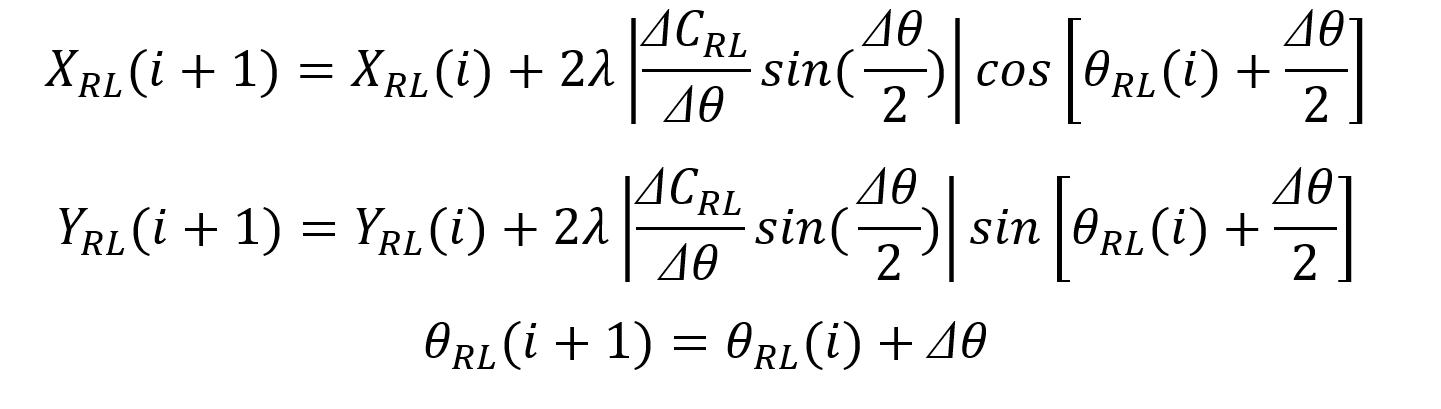
因此后轴中心的坐标偏航角为：

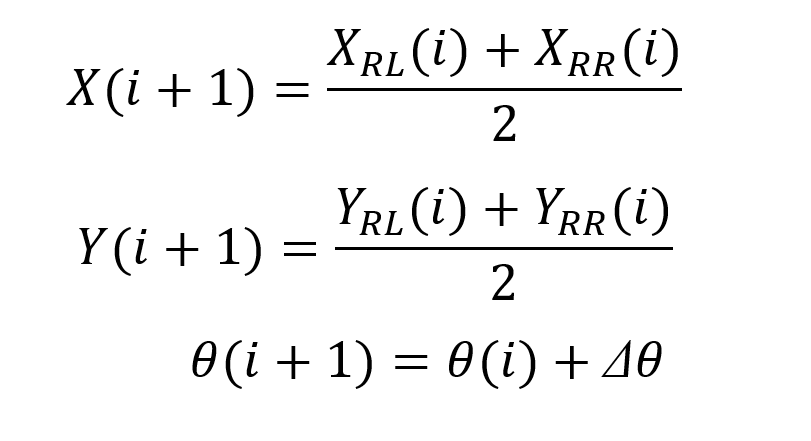
2. 方向盘转角法计算车辆位置

2.1直线行驶

直线行驶的判断依据是：

φ-方向盘转动角度，带正负；直线行驶后轴中心点的迭代算法

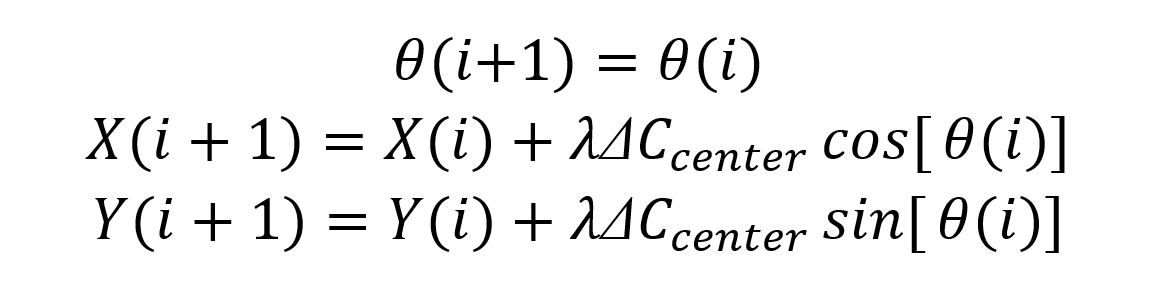
2.2曲线行驶

曲线行驶的判断依据是：

曲线行驶时，车辆后轴中心点迭代类型分为四种：

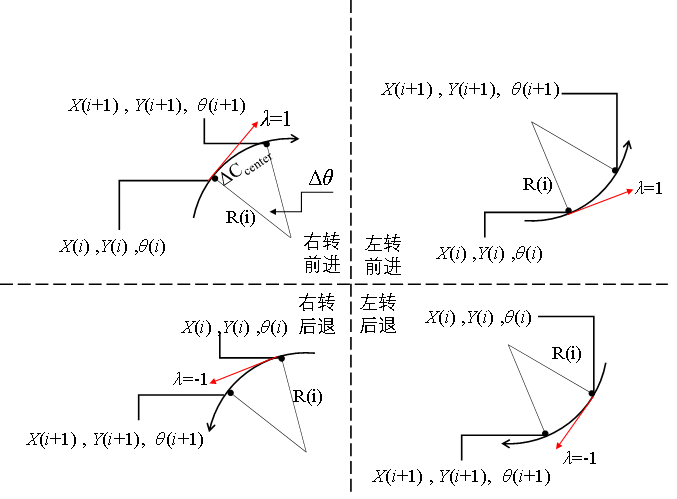
为了对上述四种类型的迭代进行统一化，规定方向盘正中位置顺时针转，角度为负；方向盘正中位置逆时针转，角度为正；车辆前进速度为正；车辆后退速度为负。可以归纳出如下的曲线行驶后轴中心点坐标偏航角的迭代算法：

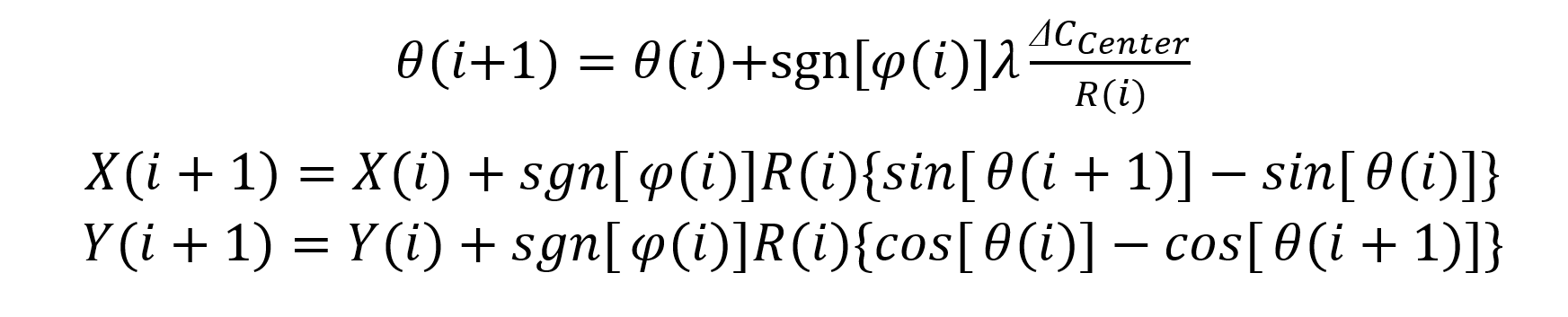
3. 脉冲法和转角法计算的精确度对比

经过大量实验验证，用方向盘转角法计算车辆相应转弯半径，利用后轴中心点行驶距离和转弯半径迭代计算会产生较大误差。原因如下：

•  由于方向盘转动时，机械系统齿轮齿条运动间隙，获得的方向盘转角并不代表此刻的车轮转角。
• 由于方向盘转动时，由于路面摩擦力和方向盘扭矩不同，导致轮胎产生不同转动响应，此时车轮转动角度会有迟滞。

脉冲法计算车辆位置可以避开车辆转弯半径参数，减少由于边走边打方向盘变半径带来的误差，通过脉冲计数计算车辆偏航角和坐标。

经过实车测试，驾驶员边走边打方向行驶7m左右距离，转角法产生40cm-50cm误差；脉冲法误差控制在10cm以内，且偏航角计算控制在1度以内。脉冲法较为准确，但仍需大量测试和改进算法提高鲁棒性，提高准确度。

方向盘转角法计算车辆位置适用于仿真工况，此时无法输入车轮脉冲，显然给仿真系统输入不同的方向盘转角便于计算分析。另外，对于定方向盘转角车辆运动也可以采用转角法。