本文主要是介绍数字IC前端学习笔记：数字乘法器的优化设计（Dadda Tree乘法器），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
相关阅读
数字IC前端
https://blog.csdn.net/weixin_45791458/category_12173698.html?spm=1001.2014.3001.5482
华莱士树仍然是一种比较规则的结构（这使得可以方便地生成树的结构），这导致了它所使用的全加器和半加器个数不是最少的，Dadda提出了一种改良华莱士树的方式，这后来被称为Dadda Tree。他使用了最少数量的全加器以及半加器来重构了树，且能保证树的级数（深度）不变，这就在节省硬件资源的情况下保证了相似的性能。
达达树的压缩策略如下算法所示。
- 令
，
，其中中括号表示向下取整。找到最大的j，使得至少一列部分积的深度大于
。
- 使用全加器或半加器去压缩那些深度超过
- 重复步骤1和2直到部分积变成只有两行或者说
。
根据这个算法，可以得到dadda的树的结构，如图1所示。图中的斜杠/代表一个全加器，连接的分别是右上角的本位和以及左下角给高位的进位，带反斜杠\的/表示是半加器。
具体的压缩过程为，首先按照规则找到最大的j为3，其中第4列（从右到左）有4列部分积，所以使用一个半加器压缩，第5列的部分积加上第4列的进位，一共有4列部分积，所以也需用一个半加器压缩。然后接着重复步骤1，找到最大的j为2，其中第3列有3列部分积，所以使用一个半加器压缩，第4列因为第3列的进位，所以有4列部分积，因此需要全加器压缩，第5、6列同理需要使用全加器压缩，得到最后2行部分积。最后使用向量合并器（可以是传播进位加法器，也可以是超前进位加法器）将部分积累加。
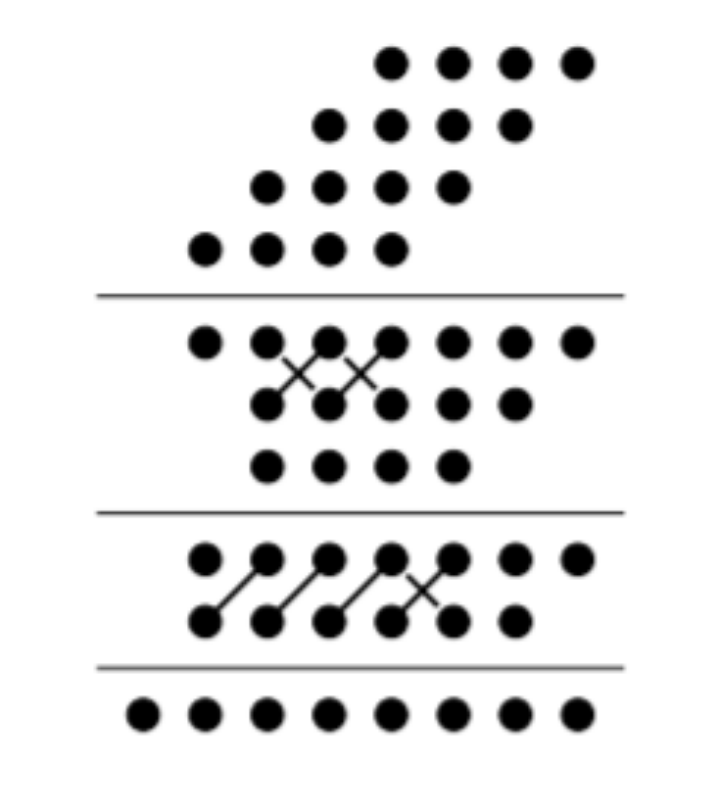
图1 dadda树乘法器的覆盖过程
具体的Verilog代码实现见附录，Modelsim软件仿真截图如图2所示。使用Synopsis的综合工具Design Compiler综合的结果如图3所示，综合使用了0.13μm工艺库。
图2 dadda树乘法器仿真结果
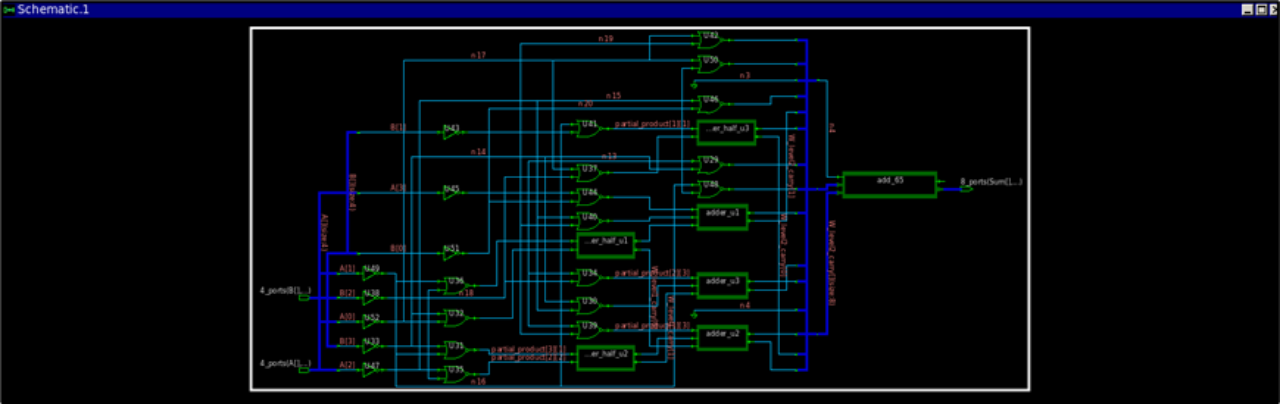图3 dadda树乘法器综合结果
在Design Compiler中使用report_timing命令，可以得到关键路径的延迟，如图4所示，可以看出延迟有1.54ns，略差于华莱士树，这是因为达达树最后的向量合并器的数据位宽较大。
图4 dadda树乘法器关键路径报告
在Design Compiler中使用report_area命令，报告所设计电路的面积占用情况，如图5所示，可以看到这个面积优于华莱士树乘法器，不考虑最后的向量合并器，达达树仅仅使用了三个全加器和三个半加器就完成了四位数据的部分积累加，相比之下，华莱士树使用了五个全加器和三个半加器，当数据位宽增加时，华莱士树乘法器对于加法器的需求增加也比达达树快，因此达达树是华莱士树的优化版，但达达树不具有华莱士树的规则的结构，设计起来会比较消耗时间和人力。
图5 dadda树乘法器面积报告
dadda树乘法器的Verilog代码如下所示。
module Dadda_Multiplier (input [3:0] A ,input [3:0] B ,output [7:0] Sum
);wire [3:0] partial_product [3:0]; wire [1:0] W_level1_c,W_level1_carry;wire [3:0] W_level2_c,W_level2_carry;wire [6:0] W_level3[0:1];//产生部分积assign partial_product[0]=B[0]?A:0;assign partial_product[1]=B[1]?A:0;assign partial_product[2]=B[2]?A:0;assign partial_product[3]=B[3]?A:0;// level1Adder_half adder_half_u1 (.Mult1 (partial_product[2][1]),.Mult2 (partial_product[3][0]),.Res (W_level1_c[0]),.Carry(W_level1_carry[0])); Adder_half adder_half_u2 (.Mult1 (partial_product[3][1]),.Mult2 (partial_product[2][2]),.Res (W_level1_c[1]),.Carry(W_level1_carry[1]));// level2Adder_half adder_half_u3 (.Mult1 (partial_product[1][1]),.Mult2 (partial_product[2][0]),.Res (W_level2_c[0] ),.Carry(W_level2_carry[0]));Adder adder_u1 (.Mult1 (partial_product[0][3]),.Mult2 (partial_product[1][2]),.I_carry (W_level1_c[0] ),.Res (W_level2_c[1] ),.Carry (W_level2_carry[1] ));Adder adder_u2 (.Mult1 (partial_product[1][3]),.Mult2 (W_level1_c[1] ),.I_carry (W_level1_carry[0] ),.Res (W_level2_c[2] ),.Carry (W_level2_carry[2] ));Adder adder_u3 (.Mult1 (partial_product[2][3]),.Mult2 (partial_product[3][2]),.I_carry (W_level1_carry[1] ),.Res (W_level2_c[3] ),.Carry (W_level2_carry[3] ));assign W_level3[0] = {partial_product[3][3], W_level2_c[3:1], partial_product[0][2:0]};assign W_level3[1] = {W_level2_carry[3:0], W_level2_c[0], partial_product[1][0], 1'b0};assign Sum = W_level3[0] + W_level3[1];endmodule这篇关于数字IC前端学习笔记：数字乘法器的优化设计（Dadda Tree乘法器）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
