广西大学东信杯第四届程序设计竞赛（同步赛）部分题解

赛题链接：牛客（NC）广西大学第四届程序设计竞赛（同步赛） 点击传送

借鉴了mrgg等诸位大佬的代码

第一次写题解，希望大佬勿喷，时间有限，错误难以避免，希望各位大佬指正

A题 Antinomy与比赛的含金量（签到题）

 签到题，给n个比赛，每个比赛有三个参数a，b，c如果a,b大于90，c大于60，输出A+，否则输出E+。

#include <iostream>
using namespace std;
int main()
{int T;scanf("%d",&T);while(T--){int a,b,c;scanf("%d%d%d",&a,&b,&c);printf("%s\n",(a>90&&b>90&&c>60)?"A+":"E+");}return 0;
}

B题 Antinomy与取模（数论）

数论入门题

两个知识点：GCD（最大公约数）、LCM（最小公倍数）

1.最大公约数GCD

整数a和b的最大公约数记为gcd（a，b）。在编程时有两种做法

（1）经典的欧几里得算法，用辗转相除法求最大公约数，模板如下：

int gcd(int a,int b){

return b==0? a:gcd(a%b);

}

时间复杂度差不多是O（log2n）的，非常快。

（2）或者直接用c++的内置函数求GCD

包含在头文件algorithm下

std::__gcd(a,b)

2.最小公倍数LCM

整数a和b的最小公倍数记为lcm(a,b),模板如下：

Int lcm(int a,int b){

Return a/gcd(a,b)*b;

}

由题意可知yi是a和b的最小公倍数的整数倍。且yi介于l和r之间。所以我可以先求得a，b的最小公倍数，记为c。由于l<=yi<=r,所以我们可以推得 l/c<=yi/c<=r/c（c=0的情况也满足）

所以让倍数i从l/c遍历到r/c，一旦i*c介于l和r之间，即可输出并跳出循环。如果遍历完还没有输出即不存在答案，输出-1。

#include<iostream>
#include<algorithm>
#define ll long long
using namespace std;
ll gcd(ll a, ll b) {return b == 0 ? a : gcd(b, a % b);
}
ll lcm(ll a, ll b) {return a / gcd(a, b) * b;
}int main() {int t;cin >> t;ll a, b, l, r;while (t--) {int flag = 0;cin >> a >> b >> l >> r;ll c = lcm(a, b);for (int i = l/ c; i <= r / c; i++) {if (l <= i*c && i*c <= r) {cout << i*c << endl;flag = 1;break;}  }if(flag==0)cout << "-1" << endl;}return 0;
}

C题 Antinomy与清理魔法（排序题）

sort函数用于C++中，对给定区间所有元素进行排序，默认为升序，也可进行降序排序。sort函数进行排序的时间复杂度为n*log2n，比冒泡之类的排序算法效率要高，sort函数包含在头文件为#include<algorithm>的c++标准库中。

由于对选择的下标没有要求，为了便于筛选，我们可以通过排序获得一个升序的整齐序列。（这样可以使得任意两个数值相近的数在空间上靠在一起）我们利用贪心的思想，遍历数组，如果前一个数减去后一个数的差值大于k，那么，输出NO并跳出循环，最后如果都满足便输出YES。

#include<bits/stdc++.h>
#define ll long long
using namespace std;const int N=5007;inline  ll read()//快读板子
{ll x=0,ch=getchar(),j=1;while(!isdigit(ch)){if(ch=='-') j=-1;ch=getchar();}while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}return x*j;
}ll n,k;
ll a[N];int main()
{n=read(),k=read();for(int i=1;i<=n;i++){a[i]=read();}  sort(a+1,a+1+n);for(int i=2;i<=n;i++){if(a[i]-a[i-1]>k){cout<<"NO";return 0;}}cout<<"YES";
}

D题 Antinomy学内存对齐

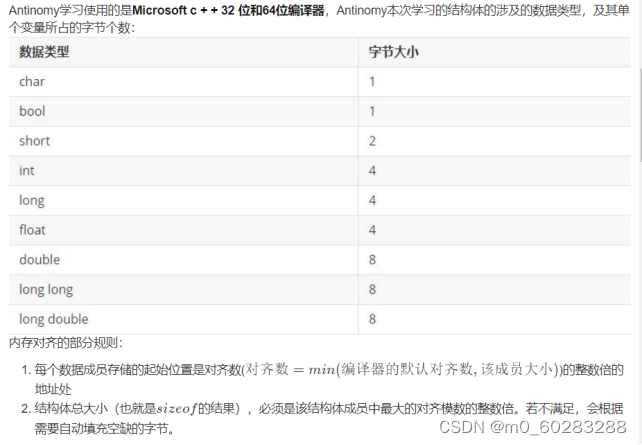
根据内存对齐的部分规则以及备注可知，默认的对齐数是4，也就是说int、long、float这些4字节和double、long long、long double这些8字节的成员可以留在最后输出（因为它们的字节数都是4的倍数）。所以只需要考虑char、bool、short这三个成员的顺序情况

即优先级：char>bool>short

如代码所示，结构体node类型数组s[maxn]中每个元素都存储一个字符串string pa和一个优先级p。每次输入一行字符串，通过判断这行字符串的首字母’c’ ‘b’ ‘s’来对这行字符串赋予优先级：即’c’为首的字符串优先级为1，最高，依次类推。

贴个代码：

#include<algorithm>
#include<iostream>
#include<cstring>
#include<string>
using namespace std;
const int maxn = 1e6 + 10;struct node {string pa;int p;
}s[maxn];
int t = 0;
string st, ed;bool cmp(node a, node b) {return a.p < b.p;
}int main() {getline(cin, st);while (getline(cin, s[++t].pa)) {string str = s[t].pa;int len = str.size();if (str == "};")break;if (str[0] == 'c')s[t].p = 1;else if (str[0] == 'b')s[t].p = 2;else if (str[0] == 's')s[t].p = 3;else s[t].p = 4;}sort(s + 1, s + t, cmp);cout << st;for (int i = 0; i < t; i++) {cout << s[i].pa<<endl;}cout << "};";return 0;
}      

E题 Antinomy慢慢点技能树(01背包)

仔细读题，每个技能最多只能点一次，也就是点或者不点两种情况。可以对应到01背包问题上来

关于01背包问题，可以参考这篇博客：动态规划之01背包问题 - kkbill - 博客园

对于每一个精确到小数点后4位的浮点数，由于不能按int类型直接处理，我们可以将它扩大1w倍，这样它就可以被当作int类型来处理了

But

很多同学发现，为什么扩大1w倍后仍然不能ac呢？这里涉及到一个小小的知识点,也就是说会出现下面这种情况：

 具体解释可以参考：组成原理|为什么计算机中0.3 + 0.6 等于 0.899999999...？ - fishers - 博客园

也就是说我们如果想要使得答案准确，需要给原来的数上加上一点数，使得它可以进位，从而不会发生如上图所示的情况。

解决这些问题后，答案就显然易见了：

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int maxn = 1e5+7;
double x[maxn];
long long w[maxn];
long long v[maxn];
ll dp[maxn];
int main(){int t = 1;while(t--) {ll n ,k;cin >> n;k = 10000;for(int i = 1; i <= n ; i++) {scanf("%lf%lld",&x[i],&v[i]);w[i] = (x[i]+0.000001)*10000;for(int j = k;j>=w[i];j--) {dp[j] = max(dp[j],dp[j - w[i]] + v[i]);}}     cout<<dp[k]<<"\n";}
}

本题解用到了滚动数组:
在处理dp[][]状态数组的时候有一个小技巧：把它变成一维的dp[]，以节省空间。观察二维表dp[][]可以发现，每一行是从上面一行算出来的，只跟上面一行有关系，跟更前面的行没有关系。那么用新的一行覆盖原来的一行就可以了。
滚动数组板子：（hdu2602）
int dp[T];
int ans(){memset(dp,0,sizeof(dp));for(int i=1;i<=N;i++)for(int j=V;j>=bone[i].vol;j--)dp[j]=max(dp[j],dp[j-bone[i].vol]+bone[i].val);return dp[V];
}

F题 Antinomy与金手指（kmp解法）

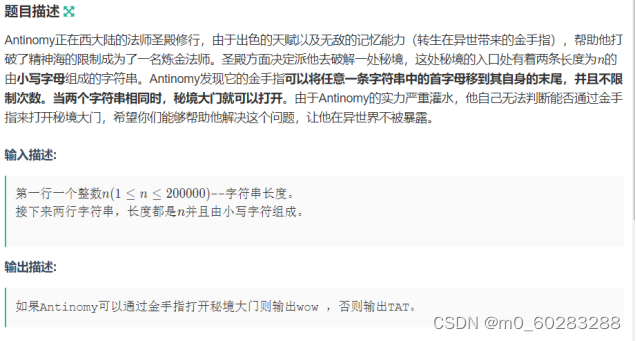
仔细读题，本题可以这样理解：

第一次输入一个字符串str

第二次输入一个字符串pattern

当时做题时，我想到了一个经典问题：石子合并问题

其中处理一段循环石子堆时，它使用了将石子堆重复两遍的方法来进行合并

所以利用这种思想，我们来处理这道题：

如str=abcde pattern=cdeab的情况时，我们可以修改str=abcdeabcde，然后判断str是否存在一段pattern序列，如果存在即满足条件。

当然可以选择暴力搜索，就是算法复杂度会很大（因为n<=2e6）

这里我选择使用kmp算法，当然大佬可以考虑更优的算法AC自动机、后缀树等，这里不做过多讲解。

Kmp算法可以参考下列这篇博客：

（原创）详解KMP算法 - 孤~影 - 博客园

贴个代码：

#include<iostream>
using namespace std;
const int MAXN = 400005;
//char str[MAXN], pattern[MAXN];
string str, pattern;
int Next[MAXN];
int cnt=0;
void getfail(string p, int plen) {Next[0] = 0; Next[1] = 0;for (int i = 1; i < plen; i++) {int j = Next[i];while (j && p[i] != p[j]) j = Next[j];Next[i + 1] = (p[i] == p[j]) ? j + 1 : 0;}
}
void kmp(string s, string p) {int last = -1;int slen = s.length(), plen = p.length();getfail(p, plen);int j = 0;for (int i = 0; i < slen; i++) {while (j && s[i] != p[j])j = Next[j];if (s[i] == p[j]) j++;if (j == plen) {if (i - last >= plen) {cnt++;last = i;}}}}
int main() {int n;cin >> n;cin >> str;str += str;cin >> pattern;kmp(str, pattern);if (cnt != 0) cout << "wow";else cout << "TAT";return 0;
}

 以上就是我对这次比赛部门题目的理解。由于太菜了，只能解释这点题目。不正确的地方希望有大佬能帮忙指正，拜托了拜托了。