本文主要是介绍LOOPS(概率dp),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

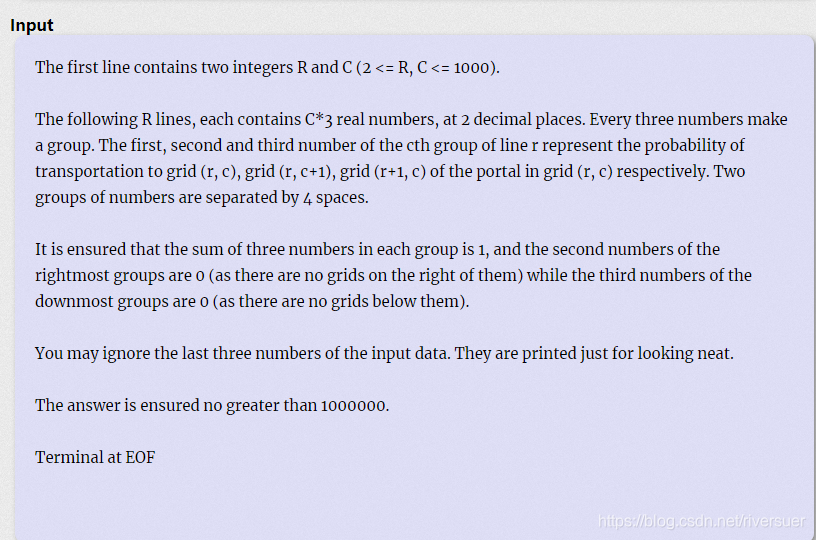

题意:
有一个r*c的迷宫,每一个位置给出向右一步,向下一步,停留原地的概率。每走一步消耗掉2能量,求从(1,1)到(r , c)需要的能量期望
思路:
用一个三维数组记录每格三种行动情况的概率
dp[i][j]来记录期望,表示从(i ,j)到(r,c)的期望值。
转移公式为:
dp[i][j]=m[i][j][1]*dp[i][j+1]+m[i][j][2]*dp[i+1][j]+dp[i][j]*m[i][j][0]+2
移项后得:
dp[i][j]=(m[i][j][1]*dp[i][j+1]+m[i][j][2]*dp[i+1][j]+2)/(1-m[i][j][0]);
+2是指新的一步消耗的能量
代码:
#include<stdio.h>
#include<math.h>
#include<string.h>
#define N 1010
double dp[N][N];
double m[N][N][3];
int main()
{int r,c;while(~scanf("%d%d",&r,&c)){memset(dp,0,sizeof(dp));int i,j,k;for(i=1; i<=r; i++)for(j=1; j<=c; j++)for(k=0; k<3; k++){scanf("%lf",&m[i][j][k]);}for(i=r; i>0; i--)for(j=c; j>0; j--){if((i==r&&j==c)||(1-m[i][j][0]==0))continue;dp[i][j]=(m[i][j][1]*dp[i][j+1]+m[i][j][2]*dp[i+1][j]+2)/(1-m[i][j][0]);}printf("%.3f\n",dp[1][1]);}return 0;
}
这篇关于LOOPS(概率dp)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



