Circuits-Combinational Logic-Arithmetic Circuits

1、Half adder

Create a half adder. A half adder adds two bits (with no carry-in) and produces a sum and carry-out.

module top_module( input a, b,output cout, sum );assign cout = a & b;assign sum 	= a ^ b;
endmodule

2、Full adder

Create a full adder. A full adder adds three bits (including carry-in) and produces a sum and carry-out.

module top_module( input a, b, cin,output cout, sum );assign cout = (a&b) | (a&cin) | (b&cin);assign sum = a ^ b ^ cin;
endmodule

3、3-bit binary adder

Now that you know how to build a full adder, make 3 instances of it to create a 3-bit binary ripple-carry adder. The adder adds two 3-bit numbers and a carry-in to produce a 3-bit sum and carry out. To encourage you to actually instantiate full adders, also output the carry-out from each full adder in the ripple-carry adder. cout[2] is the final carry-out from the last full adder, and is the carry-out you usually see.

module top_module( input [2:0] a, b,input cin,output [2:0] cout,output [2:0] sum );assign {cout[0],sum[0]} = a[0] + b[0] + cin;assign {cout[1],sum[1]} = a[1] + b[1] + cout[0];assign {cout[2],sum[2]} = a[2] + b[2] + cout[1];
endmodule

4、Adder

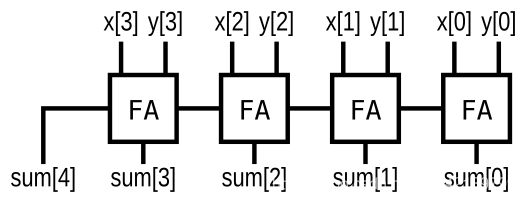
module top_module (input [3:0] x,input [3:0] y, output [4:0] sum);wire cout[2:0];assign {cout[0],sum[0]} 	= 	x[0] + y[0];assign {cout[1],sum[1]} 	= 	x[1] + y[1] + cout[0];assign {cout[2],sum[2]} 	= 	x[2] + y[2] + cout[1];assign {sum[4] ,sum[3]} 	= 	x[3] + y[3] + cout[2];
endmodule

5、Signed addition overflow

Assume that you have two 8-bit 2’s complement numbers, a[7:0] and b[7:0]. These numbers are added to produce s[7:0]. Also compute whether a (signed) overflow has occurred.
A signed overflow occurs when adding two positive numbers produces a negative result, or adding two negative numbers produces a positive result. There are several methods to detect overflow: It could be computed by comparing the signs of the input and output numbers, or derived from the carry-out of bit n and n-1.

a、b分别两个数的符号位,c为运算结果符号位。
当a =b =0（两数同为正）,而c=1(结果为负)时，负溢出；
当a =b =1（两数同为负）,而c=0(结果为正)时，正溢出.

module top_module (input [7:0] a,input [7:0] b,output [7:0] s,output overflow
); //assign s = a + b;assign overflow = (a[7]&b[7]&(~s[7])) | ((~a[7])&(~b[7])&s[7]);endmodule

6、100-bit binary adder

Create a 100-bit binary adder. The adder adds two 100-bit numbers and a carry-in to produce a 100-bit sum and carry out.

module top_module( input [99:0] a, b,input cin,output cout,output [99:0] sum );assign {cout,sum[99:0]} = a + b + cin;
endmodule

7、4-digit BCD adder

You are provided with a BCD (binary-coded decimal) one-digit adder named bcd_fadd that adds two BCD digits and carry-in, and produces a sum and carry-out.
module bcd_fadd {
input [3:0] a,
input [3:0] b,
input cin,
output cout,
output [3:0] sum );
Instantiate 4 copies of bcd_fadd to create a 4-digit BCD ripple-carry adder. Your adder should add two 4-digit BCD numbers (packed into 16-bit vectors) and a carry-in to produce a 4-digit sum and carry out.

module top_module( input [15:0] a, b,input cin,output cout,output [15:0] sum );wire [2:0] cinout;bcd_fadd a1 (a[3:0],		b[3:0],		cin,		cinout[0],	sum[3:0]);bcd_fadd a2 (a[7:4],		b[7:4],		cinout[0],	cinout[1],	sum[7:4]);bcd_fadd a3 (a[11:8],		b[11:8],	cinout[1],	cinout[2],	sum[11:8]);bcd_fadd a4 (a[15:12],		b[15:12],	cinout[2],	cout,		sum[15:12]);
endmodule

参考资料：https://hdlbits.01xz.net/