neo4j路径发现算法（Path finding algorithms）-6.The Yen’s K-shortest paths algorithm

本文主要是介绍neo4j路径发现算法（Path finding algorithms）-6.The Yen’s K-shortest paths algorithm，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一.介绍：
　　k条最短路径算法（KSP）:通常情况下，最短路径问题分为：单源最短路径和所有顶点对之间的最短路径，但两个都有一个问题，两种都只考虑两点之间最短的那一条路径，不考虑次短，再次短等路径。
　　KSP问题是对最短路径问题的推广，它除了要确定最短路径之外，还要确定次短路径、第三短路径，…，知道找到第K短路径。用Pi表示从起点s到终点t的第i短路径，KSP问题是确定路径集合Pk={p1,p2,p3,…,pk}，使得满足以下3个条件：
1）K条路径是按次序产生的，即对于所有的i（i=1,2,…,K-1），pi是在pi+1之前确定；
2）K条路径是按长度从小到大排列的，即对于所有的i（i=1,2,…,K-1），都有c(pi)<c(pi+1)；
3）这K条路径是最短的，即对于所有的p∈Pst-PK，都有c(pk)<c§。

算法思想：算出第一条最短路径p（1），然后在比基础上依次算出其他的k-1条最短路径。在求p（i+1）时，将p（i）上除了终止节点外的所有节点视为偏离节点，并计算每个偏离点到终止节点的最短路径，再与之前的p（i）上起始节点到偏离节点的路径拼接，构成候选路径，进而求得最短偏离路径。

二. neo4j算法：

CALL algo.kShortestPaths(startNode:Node, endNode:Node, k:int, weightProperty:String,
{nodeQuery:'labelName', relationshipQuery:'relationshipName', direction:'OUT',
defaultValue:1.0,
maxDepth:42, write:'true', writePropertyPrefix:'PATH_'})
YIELD resultCount, loadMillis, evalMillis, writeMillis

三 .实例:

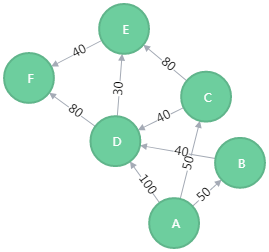
MERGE (a:Loc {name:'A'})
MERGE (b:Loc {name:'B'})
MERGE (c:Loc {name:'C'})
MERGE (d:Loc {name:'D'})
MERGE (e:Loc {name:'E'})
MERGE (f:Loc {name:'F'})
MERGE (a)-[:ROAD {cost:50}]->(b)
MERGE (a)-[:ROAD {cost:50}]->(c)
MERGE (a)-[:ROAD {cost:100}]->(d)
MERGE (b)-[:ROAD {cost:40}]->(d)
MERGE (c)-[:ROAD {cost:40}]->(d)
MERGE (c)-[:ROAD {cost:80}]->(e)
MERGE (d)-[:ROAD {cost:30}]->(e)
MERGE (d)-[:ROAD {cost:80}]->(f)
MERGE (e)-[:ROAD {cost:40}]->(f);

在这里插入图片描述

MATCH (start:Loc{name:'A'}), (end:Loc{name:'F'})
CALL algo.kShortestPaths.stream(start, end, 5, 'cost' ,{})
YIELD index, nodeIds, costs
RETURN [node in algo.getNodesById(nodeIds) | node.name] AS places,
costs,
reduce(acc = 0.0, cost in costs | acc + cost) AS totalCost

根据设置，我们得出了5条从节点A到节点F的最短路径
在这里插入图片描述