最小二乘系统辨识--WT

一、模型辨识

模型辨识就是在输入输出数据的基础上，从一组给定的模型类中，确定一个与所测系统等价的模型。模型辨识有三个要素——数据、模型和准则，辨识就是按照一个准则在一组模型类中选择一个与数据拟合得最好的模型。本文利用输入系统的扭矩信息以及输出的位置信息对系统的模型参数进行辨识。文章参考《A matlab-based identification procedure applied to a two-degrees-offreedom robot manipulator for engineering students
》。

二、模型辨识流程

|

两连杆机器人模型

1、激励轨迹

为了辨识系统的动力学特性，利用的是系统运行时采集出的数据，这些数据应具有丰富的系统特性，辨识出来的参数才能更加准确合理，而系统在一般轨迹下无法携带更多的系统信息，因此需要设计一条特殊的激励轨迹。激励轨迹设计参照《Optimal Robot Excitation and Identification》的一个有限的傅里叶级数和。

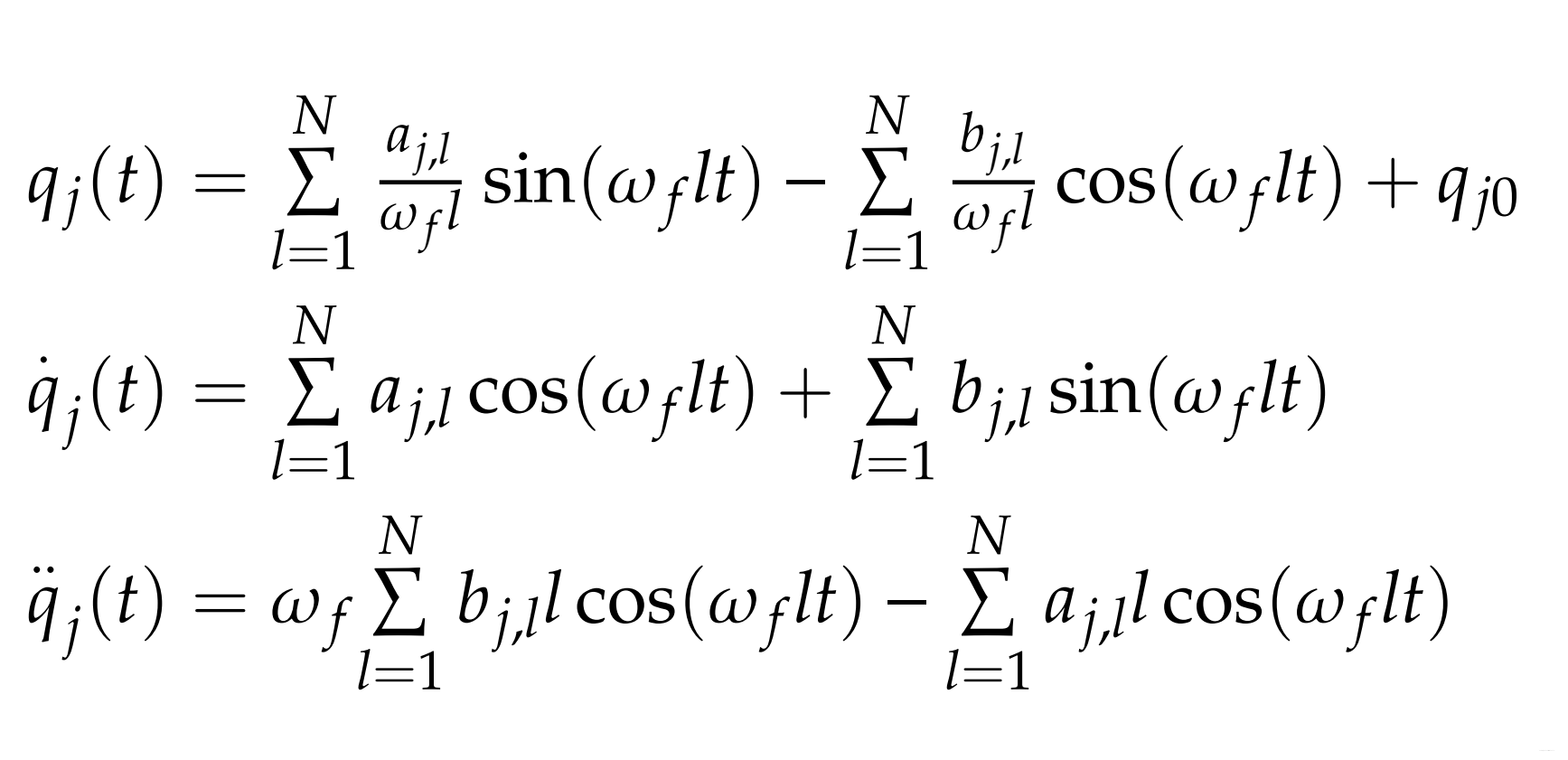
Subject mincond($\varphi$)

Constraint:

$\varphi$为系统的观测矩阵。这里以最小化观测矩阵条件数为优化目标。一般情况希望轨迹平缓且无位置、速度以及加速度的突变、且系统在低速下运行。设计对轨迹 的约束。
以上述图二连杆机器人为例，求一最优轨迹
取基频wf=0.1* pi,步长t=0.01,T=10,采样点1000，设计4次谐波分量，两连杆机器人2*N+1个参数，MATLAN 非线性优化工具箱进行求解，依据模型写出回归矩阵为：

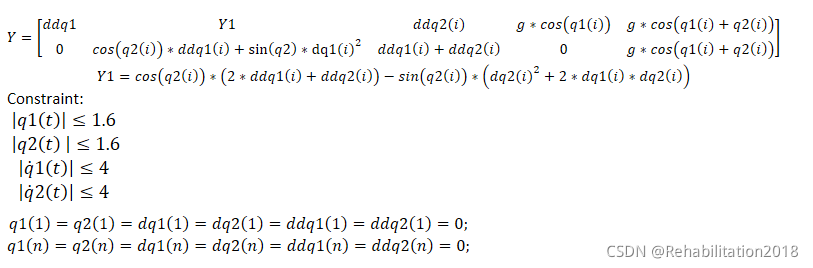
一般利用matlab中的fmincon函数进行求解：

求得多项式参数：

多项式轨迹为：

q1(i)=x(1)+x(2)sin(wft)+x(3)cos(wft)+x(4)sin(2wft)+x(5)cos(2wft)+x(11)sin(3wft)+x(12)cos(3wft)+x(15)sin(4wft)+x(16)cos(4wft);
q2(i)=x(6)+x(7)sin(wft)+x(8)cos(wft)+x(9)sin(2wft)+x(10)cos(2wft)+x(13)sin(3wft)+x(14)cos(3wft)+x(17)sin(4wft)+x(18)cos(4wft);

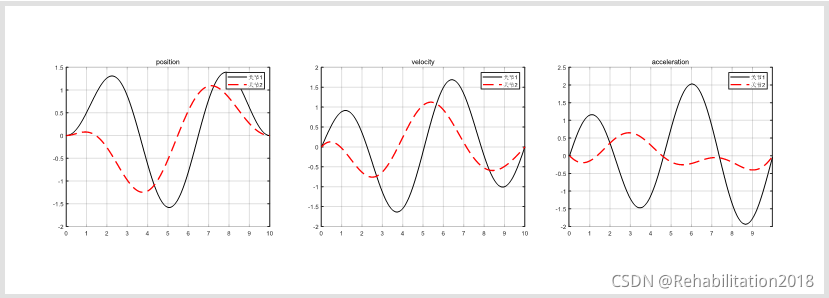
下图分别是位置、速度与加速度：

2、最小二乘法辨识轨迹：

a、最小二乘法是统计学中十分重要的一种方法，而普通最小二乘法(ordinary least squares,OLS)是其中最基础也是最常用的一种,其主要思想是每个点到拟合模型的距离最短(残差最小)时的模型为最优，但是如果使用距离直接计算则会出现正负相抵的情况，而使用绝对值进行计算则会使计算变得十分繁琐，故采用距离的平方和进行计算，故最小二乘法实际上可翻译为最小平方和法。

参考：
https://www.jianshu.com/p/8da4cf5aba5e
https://www.jianshu.com/p/d01882f5d18a
https://www.cnblogs.com/-wenli/p/11846285.html
https://my.oschina.net/keyven/blog/526010
多变量最小二乘：

我们用最后的公式便可以了，$\beta$便是我们需要辨识的参数向量。
b、 机器人动力学方程可线性化为：τ =Yβ+ERR其中Y为系统的回归矩阵、ERR代表过程控制中的误差噪声，Y使用优化轨迹中的回归矩阵，ERR使用0.5db的高斯白噪声（如下第一幅图），优化轨迹使用上述的优化轨迹，建模模型如本文第二图所示。 β=[“0.9; 0.5 ;0.8 ;0.78 ;0.7” ]。

如上图所示，为加入噪声后通过最小二乘法进行辨识的结果。下图时未加入噪声的辨识结果。

3、对《A matlab-based identification procedure applied to a two-degrees-offreedom robot manipulator for engineering students》文章的给出的数据进行了验证。

a、论文中给出的模型为：

b、利用论文中提供的扭矩以及位置信息通过最小二乘法参数辨识的结果：

3、验证：
在simulink中搭建一个PD 闭环控制器，对辨识模型进行控制，取出扭矩输出以及位置信息。

验证结果如下图所示，论文以及论文中的数据在文末给出可自行下载验证。红色虚线表示预测值，黑色虚线为文中给的采集出的位置信息，红色实线为采集与预测的误差。左下与右下方为两关节预测扭矩与论文中给出数据的对比，扭矩输出也是比较接近的。

【1】A matlab-based identification procedure applied to a two-degrees-offreedom robot manipulator for engineering students
【2】data