本文主要是介绍DTW:Dynamic Time Warping,动态时间规整,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
DTW 起源于语音识别领域,目的是衡量两个长度不同的序列的相似性(similarity),并计算两个序列之间的最佳匹配。
对于 两个长度相同的序列,其相似性可以通过一种很直接的方式衡量 —— 依次计算两个序列中各个点之间的距离,最后进行加和。
例1 :将两个序列中的点根据点在序列中的位置一一对应,即 A(1)与B(1),A(2)与B(2),... ,A(i)与B(i),... ,A(6)与B(6)相对应。
Similarity(A, B) = |A(1)-B(1)|+|A(2)-B(2)|+ ... + |A(6)-B(6)|。
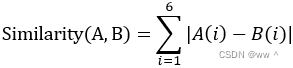

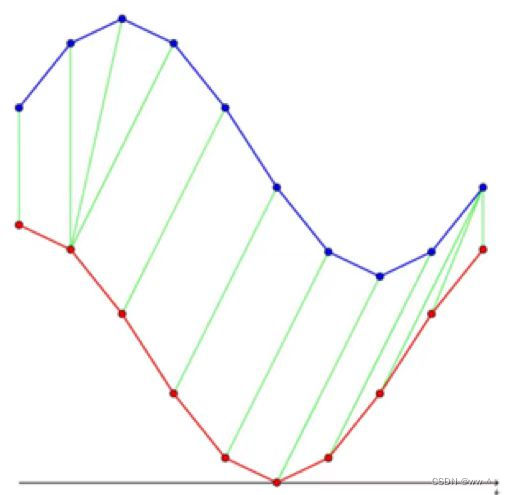
例2 :允许一个序列的点 可以与 另一个序列的多个点 对应。比如下图中,A(1)与B(1),A(2)与B(1),A(3)与B(2),A(4)与B(2),A(5)与B(3)、A(5)与B(4),A(6)与B(5)、A(6)与B(6)相对应。
Similarity(A, B) = |A(1)-B(1)| + |A(2)-B(1)| + |A(3)-B(2)| + |A(4)-B(2)| + |A(5)-B(3)| + |A(5)-B(4)| + |A(6)-B(5)| + |A(6)-B(6)|。

时间规整(Time Warping):允许 一个序列中某个点 与 另一个序列中的多个连续点 相对应。
距离矩阵法
下图用一个矩阵 M,更直观地描述 A 和 B 两个序列之间的距离。横轴表示点在A中的位置,纵轴表示点在B中的位置,格点值 M(i, j) 为两个点之间的距离。
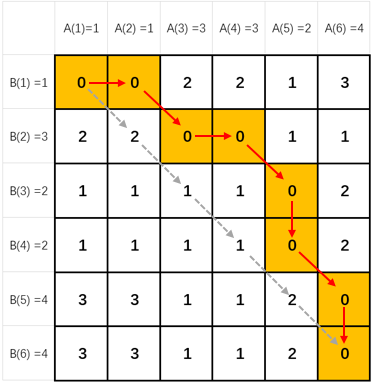
灰色虚线为 例1 所述方法,根据位置相同原则对应序列中的元素,正好是矩阵的对角线。黄格红线为 例2 。
DTW 的目标即为找到一条最短的路径。路径上的格点值之和为路径长度。DTW 的计算步骤为:① 计算两个序列中各点之间的距离矩阵 M ;② 寻找一条从矩阵的左上角到右下角的格点值之和最小的路径。
距离矩阵 M 中,从左上角到右下角的路径,具有以下性质:
① 当前路径长度 = 上一步的路径长度 + 当前格点值
② 路径上的某个格点,它的上一个格点只可能是其 左、上、左上 的某个格点。
综上所述,可以使用 递归算法 求解 最短路径长度。
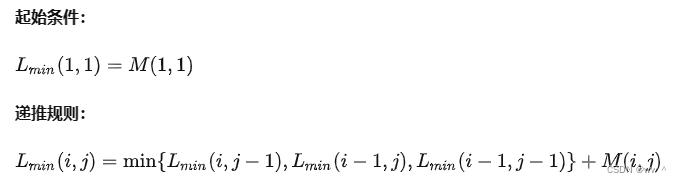
代价矩阵法
用一个矩阵 N 表示序列 A 和 B 的 cost(可以理解为两个序列之间的差异),矩阵的格点 N(i, j) 表示子序列 Ai 和 Bj 之间的cost。最小cost也可以通过递归算法求解,递推规则为:


代价矩阵法的具体算法如上表所示。首先,分别对矩阵的第一行和第一列初始化;然后,从左到右、从上到下,计算矩阵中剩下的元素。整个矩阵都计算完毕后,矩阵的右下角格点值即为这两个序列之间的最小cost。
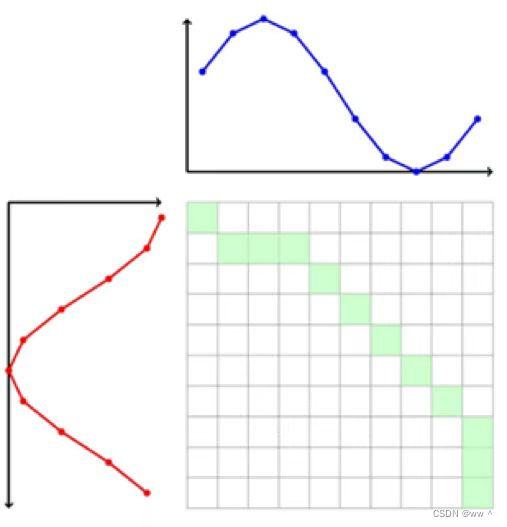
这篇关于DTW:Dynamic Time Warping,动态时间规整的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







