zkw线段树:高效的单点/区间修改+查询（原理+扩展技巧）

本文主要是介绍zkw线段树:高效的单点/区间修改+查询（原理+扩展技巧），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言

出处：清华大学张昆玮(zkw) - ppt 《统计的力量》

重口味线段树不仅比普通线段树速度快、空间小，而且码量小得多，循环结构思路也很清晰，很适合用来优化Dijkstra和套在树剖以及树套树上。

其中最重要的一点是，zkw的常数很小，仅次于树状数组。一个打得很烂的zkw，常数也不会劣于卡常卡得最好的普通线段树。（拿LOJ132为例，我的zkw和树状数组的码量差不多，跑得比所有普通线段树做法和部分树状数组做法快）

原理

重口味线段树的详细解说网上太多了，我只简单说一下，着重讲的是用法技巧（了解过普通线段树的应该很容易懂），以及一些我自己的研究。

它先开一个 MAXN*3 的数组，树形结构，底层为至少 n+2 个点，数组中点 a[i] 在树上对应节点为 tr[p+i] ，

常数 p 求法：

for(p=1;p<n+2;p<<=1);

此时得到这样一棵树：

这是个完全二叉树，tr[p+n+1]以后的点都是不存在的，即使理论探讨时认为它们存在，实际中也不能访问（这样一来空间就省到n*3）。同时由于底层有n+2个点，第一个和最后一个点都为虚点。

得到的p其实就是底层第一个虚点的编号，虚点作用会在下面提及；

树上节点关系：

tr[i]=tr[i<<1]+tr[i<<1|1];
tr[i]=max(tr[i<<1],tr[i<<1|1]);
tr[i]=min(tr[i<<1],tr[i<<1|1]);
//······

此时我们可以在输入的时候直接往 tr[p+i] 里面读入，然后往上更新，不用像某些博客里再搞个建树函数：

for(p=1;p<n+2;p<<=1);
for(int i=1;i<=n;i++)tr[p+i]=read();
for(int i=(p+n)>>1;i>0;i--)tr[i]=tr[i<<1]+tr[i<<1|1];//例如区间加
//不能从p开始更新，因为p是最底层，盲访问会出界

从叶节点往上更新（儿子节点更新父亲），相比普通线段树，省掉了从上往下找儿子节点的时间

如单点修改：

inline void change(int x,int d){for(tr[p+x]=d,x=p+x>>1;x>0;x>>=1)tr[x]=max(tr[x<<1],tr[x<<1|1]);
}

为什么重口味可以不用递归写？因为它的每个节点对应关系是严格规定的，同一深度区间大小严格相等，是一种极规范的满二叉线段树。

如图（一眼明白）：由于叶子节点的存储位置确定，不会出现普通线段树的叶子节点位置过于稀疏而浪费空间的情况（除非线段树写动态开点）。

这样既保证了从下往上搜的准确性，又避免了空间浪费。

较简单的区间修改查询（加减、最大最小）可以用差分来做（这里就不用我多说了），但是稍微复杂一点就不能用差分了，改用普通线段树？不，

永久化懒标记，弥补了重口味结构不方便区间改查的缺点。拿区间加减来说，lazy[i] 就表示 i 代表的区间需要整体加上的值，这样儿子节点就可以在往上遍历时把祖先节点的 lazy 值加上从而得到修改后的值。

关于永久化懒标记的限制，我会在后面单独说；

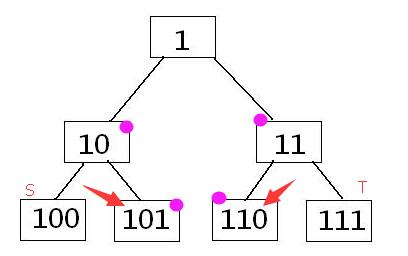
区间修改+查询时，利用到了一个规律：若需要操作的区间为 [B+1,C-1]，我们可以从区间 [A,B]，[C,D] （这里A=B，C=D，只是为了后面方便表示而用字母区分开）两个叶节点（哨兵节点）往上搜，

若 [A,B] 为右儿子，则更新为父亲 [A2,B]，（A左移），若为左儿子，则先把对应右儿子 [B+1,B2] 操作了，然后更新为 [A,B2]，（B右移）

[C,D] 则反过来，为右儿子则操作兄弟左儿子，

这里写图片描述

（骠的别人的图）

这样当更新到 [An,Bn]，[Cn,Dn]有同一父亲时（Bn==Cn-1），肯定区间 [B+1,Bn] 和 [Cn,C-1] 都被操作过了（因为没操作，所以A左移和D右移不管它）。

这里虚点的最大作用就体现出来了：当待操作的区间左端点为1时，可以从虚点0处往上向右更新；区间右端点为n时，可以从虚点n+1处往上向左更新。

板子

以区间最大值和区间求和为例

inline void add(int l,int r,int d){//区间修改for(l=p+l-1,r=p+r+1;l^1^r;){ //互为兄弟节点（有同一父亲）时停止if(~l&1)tr[l^1]+=d,lazy[l^1]+=d;//改值并搭懒标记if(r&1)tr[r^1]+=d,lazy[r^1]+=d;l>>=1,r>>=1,tr[l]=max(tr[l<<1],tr[l<<1|1])+lazy[l];//边修改边更新tr[r]=max(tr[r<<1],tr[r<<1|1])+lazy[r];}for(l>>=1;l>0;l>>=1)tr[l]=max(tr[l<<1],tr[l<<1|1])+lazy[l];//最后更新到根
}
inline int sch(int l,int r){//区间查询最大值int resl=0,resr=0;//左右两边分别记录，因为两边各自遇到的懒标记不一样for(l=p+l-1,r=p+r+1;l^1^r;){if(~l&1)resl=max(resl,tr[l^1]);if(r&1)resr=max(resr,tr[r^1]);l>>=1,r>>=1,resl+=lazy[l],resr+=lazy[r];}resl=max(resl,resr);for(l>>=1;l>0;l>>=1)resl+=lazy[l];//所有祖先的懒标记都要算上return resl;
}

//f[]是主体，lz[]是懒标记
inline void add(int l,int r,ll d){//区间加int siz=1;//维护当前层的区间的大小for(l=p+l-1,r=p+r+1;l^1^r;){if(~l&1)f[l^1]+=d*siz,lz[l^1]+=d;if(r&1)f[r^1]+=d*siz,lz[r^1]+=d;l>>=1,r>>=1,siz<<=1;f[l]=f[l<<1]+f[l<<1|1]+lz[l]*siz;f[r]=f[r<<1]+f[r<<1|1]+lz[r]*siz;}for(l>>=1,siz<<=1;l;l>>=1,siz<<=1)//更新到根f[l]=f[l<<1]+f[l<<1|1]+lz[l]*siz;
}
inline ll query(int l,int r){//查询区间和int sl=0,sr=0,siz=1; ll res=0;//分别维护左右两边查询的区间总长，以便计算懒标记的贡献for(l=p+l-1,r=p+r+1;l^1^r;){if(~l&1)res+=f[l^1],sl+=siz;if(r&1)res+=f[r^1],sr+=siz;l>>=1,r>>=1,siz<<=1;res+=lz[l]*sl+lz[r]*sr;//不是你要找的区间，但因为是祖先，所以懒标记要算入贡献}for(l>>=1,siz<<=1,sl+=sr;l;l>>=1,siz<<=1)res+=lz[l]*sl;return res;
}

上述代码看起来好像比较长，码量优势不大，但是大多数情况下用不着懒标记（包括只有区间修改单点查询的情况，原数组充当懒标记），所以码量一般是这样

inline void add(int l,int r,int d){//区间加for(l=p+l-1,r=p+r+1;l^1^r;l>>=1,r>>=1){if(~l&1)tr[l^1]+=d;if(r&1)tr[r^1]+=d;}
}
inline int schp(int x){//单点查int res=0;for(x=p+x;x>0;x>>=1)res+=tr[x];return res;
}
//又短又快

虽然重口味是从下往上搜，但是依据我使用重口味的经验，当遇到某些问题（如下，求数组中从右往左的第一个正数），也可以从上往下（其实是我懒得打普通线段树了，将就一下重口味，没想到对了！！？？！？解锁新用法！）

inline int sch(){for(int x=1,lz=0;x<=p+n;){//线段树存区间最大值 if(x>p)return tr[x]+lz>0?x-p:-1;//到底层返回lz+=lazy[x];     //累加懒标记 if(tr[x<<1|1]+lz>0)x=(x<<1|1);else x<<=1;}
}

经典优化：当我们在zkw线段树上进行单点修改的时候，如果更新不动了或没必要更新时，就直接退出，不用遍历到根。普通线段树无法实现这个优化，因为从上往下找点，回溯回去总会遍历到根。

在一些特殊的题目中，加上这个优化也许可以实现势能zkw线段树。

关于差分（upd 2021/8/20）

这应该是zkw用法中很重要的一部分，但是讲实话，我打重口味从来没用过它。懒标记板子打得太熟了。还有原数组充当懒标记的技巧，和差分一样可以省下一个数组。

这个原数组充当懒标记，上面可能没有讲清楚，所以这里再提一下。

在讲zkw维护区间加减和单点查询的时候，很多博客都说用差分。要么维护相邻两位置的差，要么维护子节点与父节点的差。维护相邻两节点差分的话，区间加是 $\log *2$ 的复杂度，单点查询变为差分数组的区间查询，也是 $\log *2$ 的复杂度，在同样思想的差分树状数组面前毫无优势。维护子节点与父节点差值，把查询优化到了一次 $\log$ ，但是代码略显繁杂。

既然只需要维护单点的值，不妨就设所有节点初值为0，然后我们只维护一个懒标记数组，相当于把zkw给“去核”。每次把一个区间搭上懒标记过后，不用往上更新，因为你不用做区间查询，所以区间和没有意义，做到两边互为兄弟节点就停止。查询的时候，只需要从叶子节点往上找，把这条链上（包括它自己）的所有懒标记加起来就是单点的值。

同样是修改 $\log *2$ ，查询 $\log$ ，“去核”的zkw和父子节点差分的zkw比较：

//差分，别人的代码
inline void add(int s,int t,int v,int A=0){for(s=s+M-1,t=t+M+1;s^t^1;s>>=1,t>>=1){if(~s&1) d[s^1]+=v;if(t&1) d[t^1]+=v;A=min(d[s],d[s^1]);d[s]-=A,d[s^1]-=A,d[s>>1]+=A;A=min(d[t],d[t^1]);d[t]-=A,d[t^1]-=A,d[t>>1]+=A;}while(s) A=min(d[s],d[s^1]),d[s]-=A,d[s^1]-=A,d[s>>=1]+=A;
}
inline int Sum(int x,int res=0){while(x) res+=d[x],x>>=1;return res;
}

//“去核”
inline void add(int l,int r,int d){for(l=p+l-1,r=p+r+1;l^1^r;l>>=1,r>>=1){if(~l&1)tr[l^1]+=d;if(r&1)tr[r^1]+=d;}
}
inline int schp(int x){int res=0;for(x=p+x;x>0;x>>=1)res+=tr[x];return res;
}
//甚至没有压行

~~（同是重口味，为何优劣如此明显）~~

这个“去核”技巧不止适用于区间加减，还可适用于各种区间操作，但是只能单点查询。

“去核”后的数组本质上是懒标记数组，所以使用时也有zkw懒标记的限制↓。

注意

重口味线段树虽然好用，但是遇到懒标记顺序不可调换的题就没办法（因为永久化懒标记是按深度从大到小依次操作，而非输入顺序），如 CodeForces 817F。

重口味还有什么限制？没有了。从整体分析，zkw线段树有且仅有这一个限制：懒标记顺序必须可任意调换。

因为这个限制，很多人觉得zkw没什么用，这显然是以偏盖全了。

标记可下传（Upd 2022.3.24）

好久没更新这篇文章了，顺便改了一些BUG。

我们知道使用永久化懒标记的zkw线段树无法处理懒标记顺序不可调换的问题，那么在思考zkw线段树应用的扩展的时候，重点肯定是想办法处理这个问题。

首先我发现，顺序不可调换的懒标记分两种：一种是完全覆盖型的，比如区间赋值，而另一种是合并型的，就是前一个和后一个合并为一个等价的懒标记。

对于第一种，我们可以记录每一步修改的内容，然后把修改的时间标号放到线段树上，就转化为了一个区间取max问题。单点查询的时候，我们只需要求出覆盖节点的时间最靠后的一个标记，这是可以永久化的。

但是第二种呢？无论如何都没办法永久化懒标记。

我知道有人会说，“zkw线段树要强制使用可下传的懒标记，那当然是理论可行的，但是太麻烦还不如普通线段树，而且常数肯定不优了吧。”

担心是合理的，但是不用想得这么悲观。事实上我们要把可下传懒标记搬到zkw线段树上，肯定不能傻傻地完全照着普通线段树这么写，要结合一下zkw线段树的性质。

zkw线段树不仅叶子节点的位置是直接可得的，而且每个叶子节点的所有祖先标号也是直接可得的。

我们知道，一个节点的父亲节点是通过节点标号除以2获得，所以叶子节点除以2的深度次方一定可以得到根节点1，而每少除以一个2就往下走一步。利用zkw线段树的性质：所有叶子结点深度相同，所以我们如果额外记录一个dep表示叶子结点的深度的话，那么把一个叶子结点x到根的一条链依次pushdown的代码就长这样：

for(int i=dep;i>0;i--)pushdown(x>>i);

是不是非常简洁？

事实上，我们只需要下传根到叶子的一条链的标记这样一个操作即可，因为我们区间修改所需要用到的懒标记只有哨兵到根的链上的。所以当我们需要区间操作的时候，我们可以先把哨兵到根的链上的标记下传，然后直接做：

inline void add(int l,int r,node tag){//区间修改 l=p+l-1,r=p+r+1;for(int i=dep;i>0;i--)pushdown(l>>i),pushdown(r>>i);//下传标记 while(l^1^r){if(~l&1)cover(l^1,tag);//覆盖懒标记 if(r&1)cover(r^1,tag);l>>=1,r>>=1,update(l),update(r);}for(l>>=1;l;l>>=1)update(l);//更新祖先 
}

这个时候就不需要考虑路径上的懒标记了，因为它们都已经被下传了。由于懒标记去永久化，所以我们的更新函数也不需要考虑懒标记。

标记可下传的zkw线段树，完成！

成功利用了zkw线段树的性质，不仅代码精简，而且速度仍然远超普通的懒标记线段树。

至此，所有一般性线段树问题，都可以用zkw线段树解决，请大家放心使用。