本文主要是介绍参数连续性与几何连续性的区别,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
曲线间连接的光滑度的度量:
- 参数连续性:组合参数曲线在连接处具有直到n阶连续导矢,即n阶连续可微,称为n阶参数连续性 C n C^n Cn
- 几何连续性:组合曲线在连接处满足不同于 C n C^n Cn的某一组约束条件,称为具有n阶几何连续性 G n G^n Gn。
对于参数 t ∈ [ 0 , 1 ] t\in[0,1] t∈[0,1]的两条曲线P(t)和Q(t)
-
若要求在结合处达到 C 0 C^0 C0连续或 G 0 G^0 G0连续,即两曲线在结合处位置连续: P ( 1 ) = Q ( 0 ) P(1)=Q(0) P(1)=Q(0)
-
若要求在结合处达到 G 1 G^1 G1连续,就是说两条曲线在结合处在满足 G 0 G^0 G0连续的条件下,并有公共的切矢: Q ′ ( 0 ) = α P ′ ( 1 ) ( α > 0 ) Q'(0)=\alpha P'(1) \ \ \ (\alpha>0) Q′(0)=αP′(1) (α>0)
- 当a=1时, G 1 G^1 G1连续就成为 C 1 C^1 C1连续
- 若P 和Q 在连接处已有 C 0 , C 1 C^0,C^1 C0,C1连续性且曲率的大小和方向均相等,即 P ′ ′ ( 1 ) = Q ′ ′ ( 0 ) P''(1)=Q''(0) P′′(1)=Q′′(0)则P 和Q 在连接处具有 C 2 C^2 C2连续
- 若P 和Q 在连接处已有 C 0 , C 1 C^0,C^1 C0,C1连续性且曲率的大小不相等但方向相等,则P 和Q 在连接处具有 G 2 G^2 G2连续。
- 当a=1时, G 1 G^1 G1连续就成为 C 1 C^1 C1连续
-
若要求在结合处达到 G 2 G^2 G2连续,就是说两条曲线在结合处在满足 G 1 G^1 G1连续的条件下,并有公共的曲率矢:
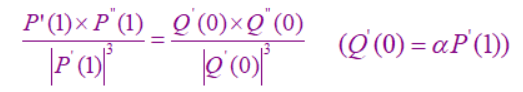
- 这个关系可写为: Q ′ ′ ( 0 ) = α 2 P ′ ′ ( 1 ) + β P ′ ( 1 ) Q''(0)=\alpha^2P''(1)+\beta P'(1) Q′′(0)=α2P′′(1)+βP′(1)
- β \beta β为任意常数,当 α = 1 , β = 0 \alpha=1,\beta=0 α=1,β=0时, G 2 G^2 G2连续就成为 C 2 C^2 C2连续
这篇关于参数连续性与几何连续性的区别的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





