[置顶] 2014训练计划

2024-09-07 19:08
文章标签 训练 计划 2014 置顶

本文主要是介绍[置顶] 2014训练计划，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

每个专题结束后会有5小时的专题赛~

1、hustOJ目前支持谷歌、火狐浏览器等部分浏览器。

2、欢迎吐槽~

3、推荐该阶段用书（以下具体算法实现多数可在此书中找到详解）：算法竞赛入门经典之训练指南(刘汝佳)

4、题解报告：专题中的题目多是经典题目，百度搜索即有详细解答~

5、专题相关知识点红字标出，建议先百度红字部分，有助于专题学习~

6、专题时间会在"ACM 今天你AC了吗？"(126270450)群中消息提醒~

7、过去的恋情和专题不要再留恋啦~，time waits no man !

8、对于图论入门：可以先记忆屈婉婷的《离散数学》图论部分（页数不是很多）了解图论，然后转跳第三步

=================================


BFS+DFS 搜索

专题链接：http://acm.hust.edu.cn/vjudge/contest/view.action?cid=39334#overview  （前5题难度稍有增强，N题是八数码推荐跳过）

（注意知识点：二进制状态压缩，队列，形参，debug，时间复杂度）

专题资料推荐：刷几个题就OK啦~(白书的入门经典)

专题赛：http://acm.hust.edu.cn/vjudge/contest/view.action?cid=39493#overview

专题概述：大家还是很热情的嘛~

-------------------------------------------------------

 

并查集、最小生成树、递推、同余

（注意知识点：树的概念、图的概念（非常重要，请自行百度））

关于图：图由点和边组成，对于n个点m条边的图（此专题下边都是无向的）我们把点标号由1-n（或0-n-1），边则通过相连的两个端点[u,v] 来区分。

关于树：对于n个点的图，我们最少需要n-1条边相连，当且仅当n个点用n-1条边相连时称为树。

显然对于树上的任意两点u、v，都有一条唯一确定的路径。

有根的称为有根树，无根的称为无根树

我们在绘制树时让根在最高处，依次向下延伸。


简述一下并查集：

并查集有2件东西：点和点所属的集合。 我们用Father[i] 表示 i 点所属的集合 为 Father[i]，（即为了区别所有的集合，我们给集合标号从1-n，在最开始时 i点属于i集合）

我们初始化每个点都不在一个集合（即相互独立） --- Father[i] = i

我们用函数(查找)：

[cpp] view plain copy print ? 在CODE上查看代码片 派生到我的代码片
  1. int find(int x){return x == Father[x] ? x : Father[x] = find(Father[x]) ; }   
int find(int x){return x == Father[x] ? x : Father[x] = find(Father[x]) ; }

来寻找 x 的最终父亲 FA， 并把路径上所有的点都归入 FA。

合并：

[cpp] view plain copy print ? 在CODE上查看代码片 派生到我的代码片
  1. void Union(int x,int y){  
  2.     int fx = find(x), fy = find(y);  
  3.     if(fx == fy)return ;  
  4.     Father[fx] = fy;  
  5. }  
void Union(int x,int y){
int fx = find(x), fy = find(y);
if(fx == fy)return ;
Father[fx] = fy;
}

对于合并过程可以用路径压缩进行优化：正确姿势是用一个rank数组（就是集合的秩"即集合元素个数"）把个数少的集合归并到集合多的集合下。

 

简述一下最小生成树：

最小生成树可以先学习kruskal (需用到并查集)

简述一下kruskal：我们先对边按权值小到大排序，然后从小到大对边判断是否选择（当且仅当边 E 所连接的端点[u,v] 不在同一集合中就说明[u,v]不相连，我们才选 E，并把 [u,v] 所在的集合归并，显然当所有点都在一个集合中，说明他们都已经被连接，则最小生成树完成）

专题链接：http://acm.hust.edu.cn/vjudge/contest/view.action?cid=39621#overview

 专题赛：http://acm.hust.edu.cn/vjudge/contest/view.action?cid=39794#overview

 专题概述：专题赛里的几个题还是很给力的~

-------------------------------------------------------

 

背包、矩阵快速幂、素数、二分查找

专题资料推荐：背包九讲，素数表的三种打发(给出一种，另一种常有的是prime[i] = true表示i为素数)，矩阵快速幂模版。

1、注意对于素数的处理，预先打出素数表这种方式我们称预处理，可以避免回答问题时对相同的结果进行重复计算。

2、若快速幂尚不理解，可转百度百科。

3、这里拓展一个分段法，可以在数据量很大但询问数很少的一类题中使用（非正规解法）相关题目及题解

专题链接：http://acm.hust.edu.cn/vjudge/contest/view.action?cid=39850#overview

专题赛：http://acm.hust.edu.cn/vjudge/contest/view.action?cid=39949#overview

 专题概述：背包是一类基础的动态规划，注意状态转移时只能从已知到未知。


-------------------------------------------------------


优先队列（最小堆）、状态压缩、单源最短路

最短路建议先学习spfa算法. 重要专题请耐心AK, 若有任何疑问可以在群里提出！

简单给出一个spfa的形式：

[cpp] view plain copy print ? 在CODE上查看代码片 派生到我的代码片
  1. int dis[N];//N个点 此处给出邻接表写法（若不熟悉可以下拉查看邻接表的示意图）   
  2. int spfa(int start, int end, int n){//最短路的起点，终点，图的下标[1,n]   
  3.     for(int i = 1; i <= n; i++)dis[i] = 100000000;  
  4.     dis[start] = 0;  
  5.     queue<int>q; q.push(start);   
  6.     while(!q.empty()){  
  7.         int u = q.front(); q.pop();  
  8.         if(u == end)continue;  
  9.         for(int i = head[u]; i!=-1; i = edge[i].next){  
  10.             int v = edge[i].to;        //遍历 以u为起点的边 的终点   
  11.             if(dis[v] > dis[u]+edge[i].dis)  {  
  12.                 dis[v] = dis[u]+edge[i].dis;  
  13.                 q.push(v);  
  14.             }  
  15.         }  
  16.     }  
  17.     return dis[end];  
  18. }  
int dis[N];//N个点 此处给出邻接表写法（若不熟悉可以下拉查看邻接表的示意图）
int spfa(int start, int end, int n){//最短路的起点，终点，图的下标[1,n]
for(int i = 1; i <= n; i++)dis[i] = 100000000;
dis[start] = 0;
queue<int>q; q.push(start); 
while(!q.empty()){
int u = q.front(); q.pop();
if(u == end)continue;
for(int i = head[u]; i!=-1; i = edge[i].next){
int v = edge[i].to;        //遍历 以u为起点的边 的终点
if(dis[v] > dis[u]+edge[i].dis)	{
dis[v] = dis[u]+edge[i].dis;
q.push(v);
}
}
}
return dis[end];
}

1、注意对于最短路中存在负环判定：对于spfa算法，当某个点入队列（入队列的意义就是该点被松弛了(更新)）次数>n次，就说明该点在负环上（可以简单证明一个点至多被更新n次(n为图中的顶点数)）。

2、优先队列：类似于堆，出队的元素不是在队尾的元素，而是队列中最小的元素（我们有时可以在队列中存储结构体元素，只需重载运算符即可）。

示例：

[cpp] view plain copy print ? 在CODE上查看代码片 派生到我的代码片
  1. struct node{  
  2.     int x, y;  
  3.     bool operator<(const node&a) const  
  4.     { if(a.x==x) return a.y<y;  return a.x<x; } //根据x,y值比较node结构体的大小   
  5. };  
struct node{
int x, y;
bool operator<(const node&a) const
{ if(a.x==x) return a.y<y;  return a.x<x; } //根据x,y值比较node结构体的大小
};

3、状态压缩：当某些状态只有true or false,时我们可以用一个整数来表示这个状态。

示例：

有3块不同的蛋糕编号1、2、3, 被老鼠啃过, 那么蛋糕只有2种状态, 我们用0表示没有被啃过, 1表示被啃过。

显然我们可以得到所有状态：000、001、010、011、100、101、110、111.

而上述二进制数对应的整数为 [0, 2^3) . （如二进制011 = 整数3表示 第2、3块蛋糕被啃过，第一块蛋糕没有被啃过）

我们可以用 for(int i = 0; i < (1<<3); i++) 来遍历所有的状态。

把多个事物的状态利用二进制含义压缩为一个整数称为状态压缩。

4、利用优先队列优化最短路时, 我们可以先出队距离起点最近的点, 则若出队的为终点显然我们已经得到了一条最短路了。

专题链接：http://acm.hust.edu.cn/vjudge/contest/view.action?cid=40014#overview

专题赛：http://acm.hust.edu.cn/vjudge/contest/view.action?cid=40141#overview

 专题概述：过年了，祝大家新年快乐~


-------------------------------------------------------

 

树的遍历、简单博弈、欧拉路径、Floyd算法

1、树的遍历分先序、中序、后序，由dfs完成（主要区别在于遍历左右子树的优先顺序和输出语句位置）

2、Floyd求传递闭包。给定邻接矩阵通过对每个点的松弛求出任意点间的距离(复杂度为O(n^3))。

3、取石子类的简单博弈可以参看此处。

简单描述一下Floyd：首先我们需要一个邻接矩阵（所谓邻接矩阵是一个 n*n 的矩阵, 第i行第j列的值为value 表示i点到j点的距离为value.若i到j点不可达时我们可以使value=inf）

注意传递闭包的概念, 得到一个传递闭包至多将任意两点松弛n次。第一层for是用k点去松弛, 第二层和第三层for是对于任意两点i、j。

Floyd代码：

[cpp] view plain copy print ? 在CODE上查看代码片 派生到我的代码片
  1. #define inf 1000000000   
  2. // init***************   
  3. for(int i = 1; i <= n; i++)  
  4.     for(int j = 1; j <= n; j++)  
  5.         dp[i][j] = inf;  
  6. //****************   
  7. //--------------Floyd:    
  8. for(int k = 1; k <= n; k++)  
  9.     for(int i = 1; i <= n; i++)if(i!=k && dp[i][k] != inf)  
  10.         for(int j = 1; j <= n; j++)if(j!=i && j!=k)  
  11.             dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j]);  
  12. //--------------   
  13. for(int i = 1; i <= n; i++) dp[i][i] = 0;  
#define inf 1000000000
// init***************
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
dp[i][j] = inf;
//****************
//--------------Floyd: 
for(int k = 1; k <= n; k++)
for(int i = 1; i <= n; i++)if(i!=k && dp[i][k] != inf)
for(int j = 1; j <= n; j++)if(j!=i && j!=k)
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j]);
//--------------
for(int i = 1; i <= n; i++) dp[i][i] = 0;

 

专题链接：http://acm.hust.edu.cn/vjudge/contest/view.action?cid=40505#overview

 

-------------------------------------------------------

（注意知识点：STL的vector容器，常用方法不多请自行百度）

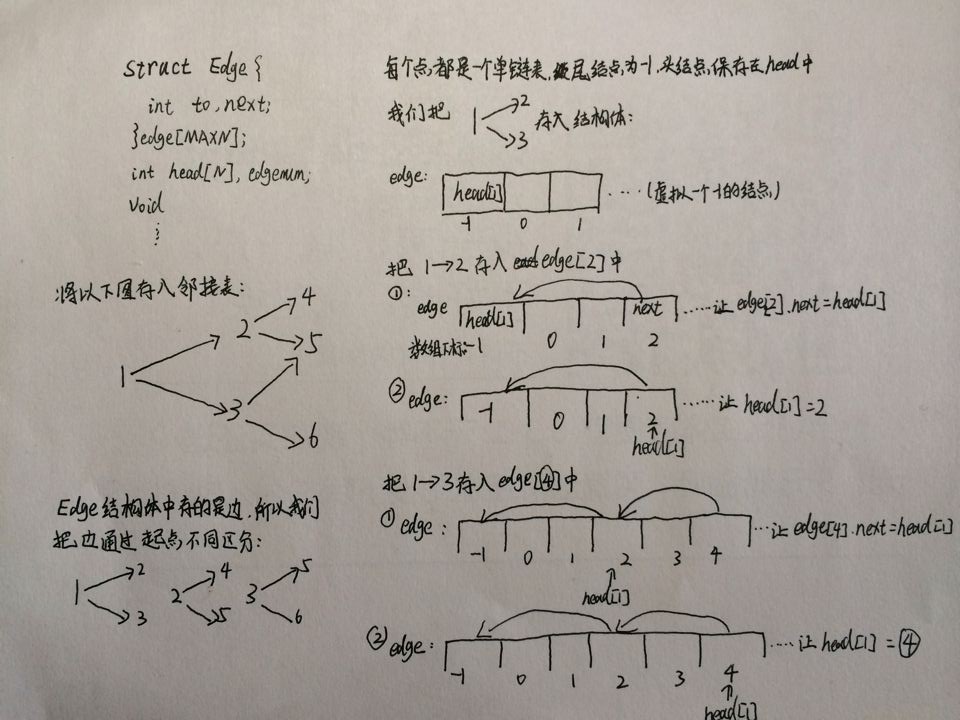
建议自学掌握基础知识：对于图的储存（邻接表、邻接矩阵）

简述下邻接表：

[cpp] view plain copy print ? 在CODE上查看代码片 派生到我的代码片
  1. struct Edge{  
  2.     int to, next;  
  3. }edge[MAXN];//MAXN为边数   
  4. int head[N], edgenum;//N为点数   
  5. void addedge(int u, int v){  
  6.     Edge E={v,head[u]};  
  7.     edge[edgenum] = E;  
  8.     head[u] = edgenum++;  
  9. }  
  10. void init(){ memset(head, -1, sizeof(head)); edgenum = 0; }//注意表头的初始化  
struct Edge{
int to, next;
}edge[MAXN];//MAXN为边数
int head[N], edgenum;//N为点数
void addedge(int u, int v){
Edge E={v,head[u]};
edge[edgenum] = E;
head[u] = edgenum++;
}
void init(){ memset(head, -1, sizeof(head)); edgenum = 0; }//注意表头的初始化

网络流、网络流求最小割、最小割定理

1、简述一下最小割：对于一个图，我们要删除一些边使得 1点与n点不连通。

删边的费用为边权值，则总边权和就是 一个可行解的割边集的权值

当费用最小时，我们称为最小割。

 

最小割 = 最大流 做一个简要证明：

我们要找一个 1点和n点的最小割 边权和（这个答案是 1点到n点的最大流）

首先我们把1、n作为源点和汇点，跑一次网络流

那么对于某条流， 显然说明了这条流是 连接着1点和n点的一条路径。

这条路径我们必须去掉，当然删除这条路径上的任意一条边就可以认为去掉了这条路径。

而这条路径上的任意边 边内的流量就是 这条路径的流量

因此为了得到删除这条路径的最小费用，我们选择这条路径上满流的边（这样不会有多余的费用产生）

此时删边的费用=边权值=流量

 

对于每条连接着1-n的路径都这样操作， 就能得到：最大流 = 最小割

 

（注意以上1点和n点只是举例，可以替换为任意两点或者任意两个点集，而非具体的定义）

补充：对于上述所说的某条路径：路径上的边必然有一条或者多条是满流的。

我们可以用反证法：假设所有边都是不满流的，此时我们还可以再在这条边上增加流量直到某条边满流为止。

 

2、网络流的建图是重点。

1）可以通过虚拟一个源点（汇点）来限制流入（流出）整个网络的流量

比如：当源点为1时，我们用 0 作为源点 并建一条 0->1 边权为C的边，这样就能限制流入流量为C。

2）当有很多个源点时，我们也可以建一个虚拟源点来连接所有源点，这样就只有1个源点了。

3）对于某个点 i ，我们可能只允许流过C流量，则此时我们把i点拆开（就是用两个点来表示i点（比如 i 和 i+N ）） 然后 i 与 i+N 中间建一条边权为C的边 来对i点限流。

3、可先学习白书的递归版dinic，然后手敲过题。

白书模版请点我。←边板子的水题请点我。

各类网络流模板：http://www.notonlysuccess.com/index.php/algorithm-of-network/

专题链接：http://acm.hust.edu.cn/vjudge/contest/view.action?cid=41551#overview

专题概述：熟悉网络流算法后可以百度下载pdf：[网络流建模汇总][Edelweiss]了解各式网络流建图方法。

-------------------------------------------------------


完全二叉树、线段树、线段树的Lazy操作

线段树资料：http://blog.csdn.net/metalseed/article/details/8039326

胡浩线段树题集及代码模式：http://www.notonlysuccess.com/index.php/segment-tree-complete/

一个木有模板的专题，请多仔细阅读资料（然后刷题）

线段树学习：

0、04年国家队论文、白书

1、建议学习胡浩版的线段树（即一个节点用一个结构体来表示

[cpp] view plain copy print ? 在CODE上查看代码片 派生到我的代码片
  1. struct node{  
  2.     int l, r;  
  3.     int val;  
  4. }tree[N*4];  
struct node{
int l, r;
int val;
}tree[N*4];
这样容易理解线段树的结构（如果不熟悉线段树的结构，可以在单步调试中watch tree这个东西，会比较清楚地看到线段树的酷炫结构，这是帮助理解的 重要一步）

本博客的线段树也是hh牛那里学习的，较容易形成模版化减少出错。

2、线段树的另一个重要功能：延迟操作

比如我们对一个数组a有2种操作

  一、区间[l,r] 每个数+ val

 二、单点求值

[cpp] view plain copy print ? 在CODE上查看代码片 派生到我的代码片
  1. struct node{  
  2.     int l, r;  
  3.     int sum, lazy;  
  4. }tree[N*4];  
struct node{
int l, r;
int sum, lazy;
}tree[N*4];

那么其实如果我们修改了1000次[1,n]区间，而在第1001次才求某点的值，那么我们不用急着把每个点更新了

而是在[1,n]这个区间做一个标记，表示这整个区间的数都被加上了一个值，那么前1000次操作都只需要对lazy修改即可。

等询问时再把这个lazy标记传到下面的区间去。

这种操作就叫延迟操作
3、线段树的延迟操作，建议写成当前区间最新，即当这个区间有lazy的标记时，这个区间也要保持最新


 专题链接：http://acm.hust.edu.cn/vjudge/contest/view.action?cid=41967#overview


-------------------------------------------------------


2-SAT、简单博弈

（注意知识点：对STL的set集合学习）

set用法简介：wenku.baidu.com/view/b71a8b524431b90d6c85c746.html

2-sat的简要在↓前面，一般可以用dfs或者tarjan缩点判断，这里暂且推荐dfs版本，较容易理解且编程复杂度不会太高。

2-sat 白书模版

专题链接：http://acm.hust.edu.cn/vjudge/contest/view.action?cid=42657#overview


-------------------------------------------------------


字典树、KMP

字典树：一个重要特色就是省内存, 多个前缀相同的字符串只需要记录一次（言外之意：对于某节点的所有子树，他们的字符串都是有公共前缀的）

字典树资料：百度百科

字典树模版：blog.csdn.net/acmmmm/article/details/12250267

字典树的代码建议先学习白书的版本。

简述一下字典树：

对于以下的5个字符串，我们用普通的方法需要16个字节储存。

********************************************************

1、abcd

2、abd

3、bcd

4、efg

5、hij

********************************************************

我们观察字符串 1、2，发现他们有公共的前缀 "ab", 所以我们可以用一个"ab"来表示所有公共前缀为"ab"的字符串。（这样我们只需要用14个字节储存）

想象一下，那么对于某一个节点u来说，u的所有子节点都是有相同的公共前缀。

对于u这个节点，我们需要记录的是u的26个子节点（因为有26个字母嘛）

对于每个节点，为了区别他们，用一个整数表示一个节点。

数组：int ch[u][26]; 表示u节点 的26个指针。例如：我们要查找 （u 接下来的字母为a）则 用 ch[u][ 0 ] 表示即可。（而接下来的字母为 z 则用ch[u][25]表示。）

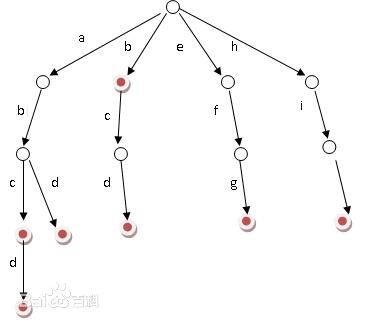
注意：因为每个字符串的第一个字母都不一定相同，所以我们虚拟一个根节点来连接所有字符串的第一个字母（下图中空白点就是虚拟节点）

（注：字母是表示箭头下方的节点）

对于某个节点，我们都能直接确定一个序列（则对于一个整数（上面提到一个节点用一个整数来表示）就能直接确定一个序列）



此时我们用 int Have_word[u]; 表示 u 这个（整数）序列的单词有多少个。

则每次插入单词时，在单词最后一个字母所在的整数 v ，Have_word[v] ++;

（如上例子在每个节点记录信息来实现字典树上的各种功能）

注意：对于任意一个节点，都是确定的一个字符串序列。


KMP：推荐先围观白书的211页

KMP个人简介（纯粹广告）：blog.csdn.net/acmmmm/article/details/9863495

KMP其他资料：blog.csdn.net/yaochunnian/article/details/7059486

KMP的复杂度是线性的，即O(n+m);

关于KMP的2个版本:普通KMP的失配数组 next[0] = 0, 滑步函数优化的失配数组 next[0] = -1;

这里推荐先学习普通版本KMP，滑步函数据说速度稍快，但失去了KMP本身的含义，且普通KMP的速度对于比赛已经足够快了。


专题链接：http://acm.hust.edu.cn/vjudge/contest/view.action?cid=43273#overview


-------------------------------------------------------


有向图的强连通分量、缩点

 强连通是对有向图求环的算法，tarjan（相当于dfs）

主要是环具有些特性，因此把环视为一个点，对图中环进行缩点，并给图重新标号

模版性较强。

强连通算法可参考白书319页 或 这里

更高端的在这里：www.byvoid.com/blog/scc-tarjan/

强连通模版

专题链接：http://acm.hust.edu.cn/vjudge/contest/view.action?cid=44430#overview

-------------------------------------------------------

 
Current： 

RMQ问题、LCA转RMQ、树状数组

RMQ问题：区间求最值，可以用线段树等解决; 详见白书197页

LCA：最近公共祖先，可以用离线的tarjan，在线的LCA转RMQ（预处理O(nlogn),询问O(1)，LCA倍增法（预处理O(nlogn),询问O(logn)）

模版变动不大，主要多做题。


树状数组：对于一个数组，可以区间求和，支持单点更新，复杂度均为O(logn); 详见白书194页

简述一下树状数组：

int c[N], maxn; //maxn的值为区间的最大值

树状数组中调用的lowbit(x) = x的二进制下后面0的个数 +1 lowbit(1)=1; lowbit(2)=2;lowbit(3)=1; 

第二个函数 void change(int pos, int val){} //给数组下标为pos的 a[pos]+=val;

第三个函数 int sum(int pos){} //[1,pos]区间的和 等价于 int ans = 0; for(int i = 1; i <= pos; i++) ans += a[i]; return ans;

注意初始化 void init(){memset(c, 0, sizeof c); maxn = n;}

树状数组的代码量较小，且有点模版化，模版改动不大，可以先试着套模版多过题再了解。

注意：若要求区间[0,pos]的和，0 这个点特殊处理一下就好。

LCA题集 

LCA倍增法模版

LCA转RMQ解法示意

专题链接：http://acm.hust.edu.cn/vjudge/contest/view.action?cid=44921#overview

-------------------------------------------------------



·数位dp、单调队列、滚动数组、费用流


简述一下费用流：

对于一个网络流，其实我们满流有多种不同的方法，如下图我们有两种方法使得满流。

有时流过一些边需要一定的费用，则我们希望在满流的情况下费用最少，就是最小费用最大流。

我们只需把白书上的dinic的BFS找一条可行流的代码改成spfa（最短路，源汇点为起末点，费用为边权，找一条费用最小的（就是最短路）进行增广）

 边的总费用=边费用*边流量。

-------------------------------------------------------

乘法逆元：

(a / b)%mod  =  a * (b^(mod-2))

b^(mod-2)套个快速幂，复杂度是log(mod), 基本是一个常数。



-------------------------------------------------------

·无向图的割顶和桥、树的重心

 

-------------------------------------------------------

 

·无向图的双连通分量


-------------------------------------------------------

 

·拓展欧几里德、AC自动机

 

-------------------------------------------------------

 

·二分匹配、基数排序

二分匹配的图论相关：（1）（2）

 二分匹配的定义：（1）

-------------------------------------------------------

 

·后缀数组

 

-------------------------------------------------------

 

 ·次小生成树、区间dp

 

-------------------------------------------------------

 当current走到这里时，再往前看，看以前的题和以前的自己，一定会惊讶自己走了这么远~

这篇关于[置顶] 2014训练计划的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/1145900。

相关文章

ZOJ Monthly, August 2014小记

ZOJ Monthly, August 2014小记

最近太忙太忙，只能抽时间写几道简单题。不过我倒是明白要想水平提高不看题解是最好的了。 A  我只能死找规律了，无法证明 int a[50002][2] ;vector< vector<int> > gmax , gmin ;int main(){int n , i , j , k , cmax , cmin ;while(cin>>n){/* g
阅读更多...
2014 Multi-University Training Contest 8小记

2014 Multi-University Training Contest 8小记

1002 计算几何 最大的速度才可能拥有无限的面积。 最大的速度的点 求凸包， 凸包上的点（ 注意不是端点 ） 才拥有无限的面积 注意 ：  凸包上如果有重点则不满足。 另外最大的速度为0也不行的。 int cmp(double x){if(fabs(x) < 1e-8) return 0 ;if(x > 0) return 1 ;return -1 ;}struct poin
阅读更多...
2014 Multi-University Training Contest 7小记

2014 Multi-University Training Contest 7小记

1003   数学 ， 先暴力再解方程。 在b进制下是个2 ， 3 位数的 大概是10000进制以上 。这部分解方程 2-10000 直接暴力 typedef long long LL ;LL n ;int ok(int b){LL m = n ;int c ;while(m){c = m % b ;if(c == 3 || c == 4 || c == 5 ||
阅读更多...
2014 Multi-University Training Contest 6小记

2014 Multi-University Training Contest 6小记

1003  贪心 对于111...10....000 这样的序列，  a 为1的个数，b为0的个数，易得当 x= a / (a + b) 时 f最小。 讲串分成若干段  1..10..0   ,  1..10..0 ,  要满足x非递减 。  对于 xi > xi+1  这样的合并 即可。 const int maxn = 100008 ;struct Node{int
阅读更多...
MiniGPT-3D, 首个高效的3D点云大语言模型，仅需一张RTX3090显卡，训练一天时间，已开源

MiniGPT-3D, 首个高效的3D点云大语言模型，仅需一张RTX3090显卡，训练一天时间，已开源

项目主页：https://tangyuan96.github.io/minigpt_3d_project_page/ 代码：https://github.com/TangYuan96/MiniGPT-3D 论文：https://arxiv.org/pdf/2405.01413 MiniGPT-3D在多个任务上取得了SoTA，被ACM MM2024接收，只拥有47.8M的可训练参数，在一张RTX
阅读更多...
Spark MLlib模型训练—聚类算法 PIC(Power Iteration Clustering)

Spark MLlib模型训练—聚类算法 PIC(Power Iteration Clustering)

Spark MLlib模型训练—聚类算法 PIC(Power Iteration Clustering) Power Iteration Clustering (PIC) 是一种基于图的聚类算法，用于在大规模数据集上进行高效的社区检测。PIC 算法的核心思想是通过迭代图的幂运算来发现数据中的潜在簇。该算法适用于处理大规模图数据，特别是在社交网络分析、推荐系统和生物信息学等领域具有广泛应用。Spa
阅读更多...
SigLIP——采用sigmoid损失的图文预训练方式

SigLIP——采用sigmoid损失的图文预训练方式

SigLIP——采用sigmoid损失的图文预训练方式 FesianXu 20240825 at Wechat Search Team 前言 CLIP中的infoNCE损失是一种对比性损失，在SigLIP这个工作中，作者提出采用非对比性的sigmoid损失，能够更高效地进行图文预训练，本文进行介绍。如有谬误请见谅并联系指出，本文遵守CC 4.0 BY-SA版权协议，转载请联系作者并注
阅读更多...
Detectorn2预训练模型复现：数据准备、训练命令、日志分析与输出目录

Detectorn2预训练模型复现：数据准备、训练命令、日志分析与输出目录

Detectorn2预训练模型复现：数据准备、训练命令、日志分析与输出目录 在深度学习项目中，目标检测是一项重要的任务。本文将详细介绍如何使用Detectron2进行目标检测模型的复现训练，涵盖训练数据准备、训练命令、训练日志分析、训练指标以及训练输出目录的各个文件及其作用。特别地，我们将演示在训练过程中出现中断后，如何使用 resume 功能继续训练，并将我们复现的模型与Model Zoo中的
阅读更多...
《计算机视觉工程师养成计划》 ·数字图像处理·数字图像处理特征·概述~

《计算机视觉工程师养成计划》 ·数字图像处理·数字图像处理特征·概述~

1 定义         从哲学角度看：特征是从事物当中抽象出来用于区别其他类别事物的属性集合，图像特征则是从图像中抽取出来用于区别其他类别图像的属性集合。         从获取方式看：图像特征是通过对图像进行测量或借助算法计算得到的一组表达特性集合的向量。 2 认识         有些特征是视觉直观感受到的自然特征，例如亮度、边缘轮廓、纹理、色彩等。         有些特征需要通
阅读更多...
多云架构下大模型训练的存储稳定性探索

多云架构下大模型训练的存储稳定性探索

一、多云架构与大模型训练的融合 （一）多云架构的优势与挑战 多云架构为大模型训练带来了诸多优势。首先，资源灵活性显著提高，不同的云平台可以提供不同类型的计算资源和存储服务，满足大模型训练在不同阶段的需求。例如，某些云平台可能在 GPU 计算资源上具有优势，而另一些则在存储成本或性能上表现出色，企业可以根据实际情况进行选择和组合。其次，扩展性得以增强，当大模型的规模不断扩大时，单一云平
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2