本文主要是介绍【算法思想·二叉树】思路篇,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本文参考labuladong算法笔记[东哥带你刷二叉树(思路篇) | labuladong 的算法笔记]
本文承接 【算法思想·二叉树】纲领篇,先复述一下前文总结的二叉树解题总纲:
二叉树解题的思维模式分两类:
1、是否可以通过遍历一遍二叉树得到答案?如果可以,用一个 traverse 函数配合外部变量来实现,这叫「遍历」的思维模式。
2、是否可以定义一个递归函数,通过子问题(子树)的答案推导出原问题的答案?如果可以,写出这个递归函数的定义,并充分利用这个函数的返回值,这叫「分解问题」的思维模式。
无论使用哪种思维模式,你都需要思考:
如果单独抽出一个二叉树节点,它需要做什么事情?需要在什么时候(前/中/后序位置)做?其他的节点不用你操心,递归函数会帮你在所有节点上执行相同的操作。
1、翻转二叉树
输入一个二叉树根节点 root,让你把整棵树镜像翻转,比如输入的二叉树如下:
4
/ \
2 7
/ \ / \
1 3 6 9
算法原地翻转二叉树,使得以 root 为根的树变成:
4
/ \
7 2
/ \ / \
9 6 3 1
【思路】
不难发现,只要把二叉树上的每一个节点的左右子节点进行交换,最后的结果就是完全翻转之后的二叉树。
那么现在开始在心中默念二叉树解题总纲:
1、这题能不能用「遍历」的思维模式解决?
可以,我写一个 traverse 函数遍历每个节点,让每个节点的左右子节点颠倒过来就行了。
单独抽出一个节点,需要让它做什么?让它把自己的左右子节点交换一下。
需要在什么时候做?好像前中后序位置都可以。
综上,可以写出如下[遍历]解法代码:
class Solution:# 主函数def invertTree(self, root):# 遍历二叉树,交换每个节点的子节点self.traverse(root)return root# 二叉树遍历函数def traverse(self, root):if not root:return # *** 前序位置 ***# 每一个节点需要做的事就是交换它的左右子节点tmp = root.leftroot.left = root.rightroot.right = tmp# 遍历框架,去遍历左右子树的节点self.traverse(root.left)self.traverse(root.right)你把前序位置的代码移到后序位置也可以,但是直接移到中序位置是不行的,需要稍作修改,这应该很容易看出来吧,我就不说了。
按理说,这道题已经解决了,不过为了对比,我们再继续思考下去。
2、这题能不能用「分解问题」的思维模式解决?
我们尝试给 invertTree 函数赋予一个定义:
# 定义:将以 root 为根的这棵二叉树翻转,返回翻转后的二叉树的根节点
def invertTree(root: TreeNode)然后思考,对于某一个二叉树节点 x 执行 invertTree(x),你能利用这个递归函数的定义做点啥?
我可以用 invertTree(x.left) 先把 x 的左子树翻转,再用 invertTree(x.right) 把 x 的右子树翻转,最后把 x 的左右子树交换,这恰好完成了以 x 为根的整棵二叉树的翻转,即完成了 invertTree(x) 的定义。
直接写出[分解]思路代码:
class Solution:# 定义:将以 root 为根的这棵二叉树翻转,返回翻转后的二叉树的根节点def invertTree(self, root):if root is None:return None# 利用函数定义,先翻转左右子树left = self.invertTree(root.left)right = self.invertTree(root.right)# 然后交换左右子节点root.left, root.right = right, left# 和定义逻辑自恰:以 root 为根的这棵二叉树已经被翻转,返回 rootreturn root这种「分解问题」的思路,核心在于你要给递归函数一个合适的定义,然后用函数的定义来解释你的代码;如果你的逻辑成功自恰,那么说明你这个算法是正确的。
好了,这道题就分析到这,「遍历」和「分解问题」的思路都可以解决,看下一道题。
2、填充节点的右侧指针
116. 填充每个节点的下一个右侧节点指针 | 力扣 | LeetCode |
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {int val;Node *left;Node *right;Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
示例 1:

输入:root = [1,2,3,4,5,6,7] 输出:[1,#,2,3,#,4,5,6,7,#] 解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化的输出按层序遍历排列,同一层节点由 next 指针连接,'#' 标志着每一层的结束。
示例 2:
输入:root = [] 输出:[]
提示:
- 树中节点的数量在
[0, 212 - 1]范围内 -1000 <= node.val <= 1000
进阶:
- 你只能使用常量级额外空间。
- 使用递归解题也符合要求,本题中递归程序占用的栈空间不算做额外的空间复杂度。
【思路】
题目的意思就是把二叉树的每一层节点都用 next 指针连接起来:
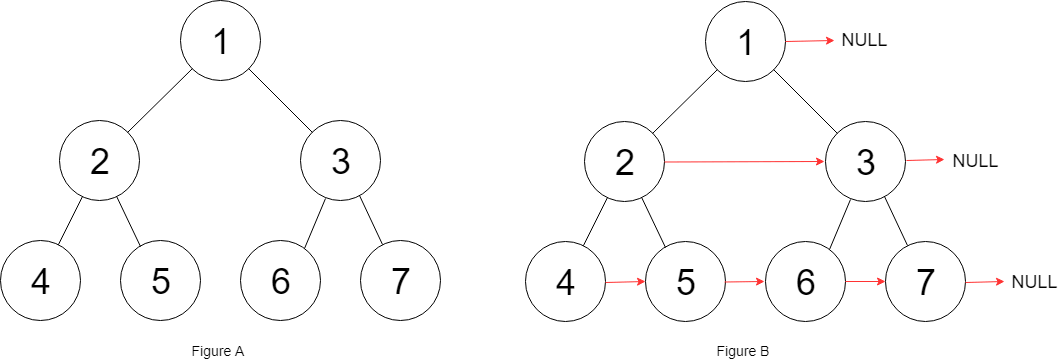
而且题目说了,输入是一棵「完美二叉树」,形象地说整棵二叉树是一个正三角形,除了最右侧的节点 next 指针会指向 null,其他节点的右侧一定有相邻的节点。
这道题怎么做呢?来默念二叉树解题总纲:
1、这题能不能用「遍历」的思维模式解决?
很显然,一定可以。
每个节点要做的事也很简单,把自己的 next 指针指向右侧节点就行了。
也许你会模仿上一道题,直接写出如下代码:
# 二叉树遍历函数
def traverse(root):if root is None or root.left is None:return# 把左子节点的 next 指针指向右子节点root.left.next = root.righttraverse(root.left)traverse(root.right)但是,这段代码其实有很大问题,因为它只能把相同父节点的两个节点穿起来,再看看这张图:

节点 5 和节点 6 不属于同一个父节点,那么按照这段代码的逻辑,它俩就没办法被穿起来,这是不符合题意的,但是问题出在哪里?
传统的 traverse 函数是遍历二叉树的所有节点,但现在我们想遍历的其实是两个相邻节点之间的「空隙」。
所以我们可以在二叉树的基础上进行抽象,你把图中的每一个方框看做一个节点:

这样,一棵二叉树被抽象成了一棵三叉树,三叉树上的每个节点就是原先二叉树的两个相邻节点。
现在,我们只要实现一个 traverse 函数来遍历这棵三叉树,每个「三叉树节点」需要做的事就是把自己内部的两个二叉树节点穿起来:
class Solution:# 主函数def connect(self, root: 'Node') -> 'Node':if not root:return None# 遍历「三叉树」,连接相邻节点self.traverse(root.left, root.right)return root# 三叉树遍历框架def traverse(self, node1: 'Node', node2: 'Node') -> None:if not node1 or not node2:return# 前序位置 # 将传入的两个节点穿起来node1.next = node2 # 连接相同父节点的两个子节点self.traverse(node1.left, node1.right)self.traverse(node2.left, node2.right)# 连接跨越父节点的两个子节点self.traverse(node1.right, node2.left)这样,traverse 函数遍历整棵「三叉树」,将所有相邻节的二叉树节点都连接起来,也就避免了我们之前出现的问题,把这道题完美解决。
2、这题能不能用「分解问题」的思维模式解决?
嗯,好像没有什么特别好的思路,所以这道题无法使用「分解问题」的思维来解决
3、将二叉树展开为链表
114. 二叉树展开为链表 | 力扣 | LeetCode |
给你二叉树的根结点 root ,请你将它展开为一个单链表:
- 展开后的单链表应该同样使用
TreeNode,其中right子指针指向链表中下一个结点,而左子指针始终为null。 - 展开后的单链表应该与二叉树 先序遍历 顺序相同。
示例 1:

输入:root = [1,2,5,3,4,null,6] 输出:[1,null,2,null,3,null,4,null,5,null,6]
示例 2:
输入:root = [] 输出:[]
示例 3:
输入:root = [0] 输出:[0]
提示:
- 树中结点数在范围
[0, 2000]内 -100 <= Node.val <= 100
进阶:你可以使用原地算法(O(1) 额外空间)展开这棵树吗?
【思路】
# 函数签名如下
def flatten(root: TreeNode)1、这题能不能用「遍历」的思维模式解决?
乍一看感觉是可以的:对整棵树进行前序遍历,一边遍历一边构造出一条「链表」就行了:
# 虚拟头节点,dummy.right 就是结果
dummy = TreeNode(-1)
# 用来构建链表的指针
p = dummydef traverse(root: TreeNode):if root is None:return# 前序位置p.right = TreeNode(root.val)p = p.righttraverse(root.left)traverse(root.right)但是注意 flatten 函数的签名,返回类型为 void,也就是说题目希望我们在原地把二叉树拉平成链表。
这样一来,没办法通过简单的二叉树遍历来解决这道题了
2、这题能不能用「分解问题」的思维模式解决?
我们尝试给出 flatten 函数的定义:
# 定义:输入节点 root,然后 root 为根的二叉树就会被拉平为一条链表
def flatten(self, root: TreeNode) -> None:有了这个函数定义,如何按题目要求把一棵树拉平成一条链表?
对于一个节点 x,可以执行以下流程:
1、先利用 flatten(x.left) 和 flatten(x.right) 将 x 的左右子树拉平。
2、将 x 的右子树接到左子树下方,然后将整个左子树作为右子树。

这样,以 x 为根的整棵二叉树就被拉平了,恰好完成了 flatten(x) 的定义。
直接看[分解]思路代码实现:
class Solution:# 定义:将以 root 为根的树拉平为链表def flatten(self, root) -> None:# base caseif root is None:return# 利用定义,把左右子树拉平self.flatten(root.left)self.flatten(root.right)# 后序遍历位置# 1、左右子树已经被拉平成一条链表left = root.leftright = root.right# 2、将左子树作为右子树root.left = Noneroot.right = left# 3、将原先的右子树接到当前右子树的末端p = rootwhile p.right is not None:p = p.rightp.right = right 你看,这就是递归的魅力,你说 flatten 函数是怎么把左右子树拉平的?
不容易说清楚,但是只要知道 flatten 的定义如此并利用这个定义,让每一个节点做它该做的事情,然后 flatten 函数就会按照定义工作。
至此,这道题也解决了,我们前文 k个一组翻转链表 的递归思路和本题也有一些类似。
最后,首尾呼应,再次默写二叉树解题总纲。
二叉树解题的思维模式分两类:
1、是否可以通过遍历一遍二叉树得到答案?如果可以,用一个 traverse 函数配合外部变量来实现,这叫「遍历」的思维模式。
2、是否可以定义一个递归函数,通过子问题(子树)的答案推导出原问题的答案?如果可以,写出这个递归函数的定义,并充分利用这个函数的返回值,这叫「分解问题」的思维模式。
无论使用哪种思维模式,你都需要思考:
如果单独抽出一个二叉树节点,它需要做什么事情?需要在什么时候(前/中/后序位置)做?其他的节点不用你操心,递归函数会帮你在所有节点上执行相同的操作。
希望你能仔细体会,并运用到所有二叉树题目上。
这篇关于【算法思想·二叉树】思路篇的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







