本文主要是介绍不容错过!最简单的Cursor无限注册攻略!,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 前言
- 具体用法
- 下载程序
- 登陆授权
- 查看支持的模型
- 如何使用
- 引用
前言
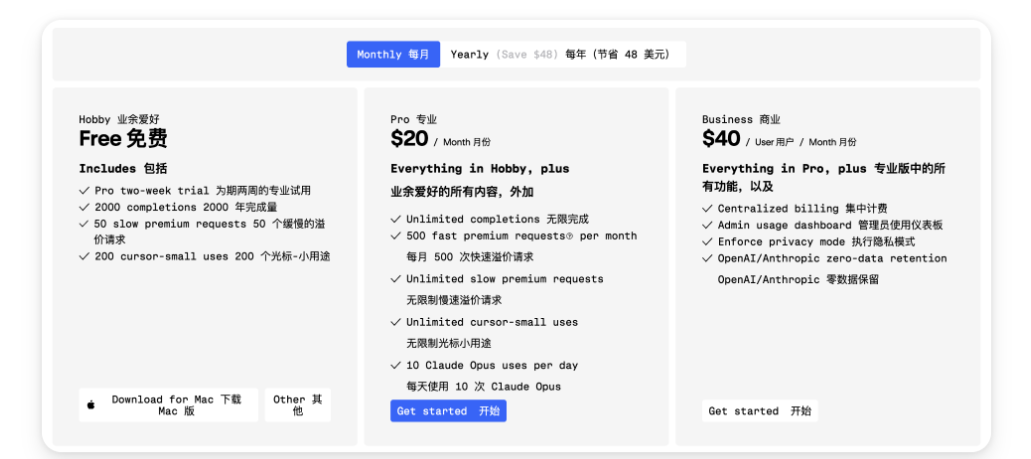
Cursor 是一个编程软件,就像Vscode一样,可以让你轻松地编写、调试和运行代码。不一样的是它内置了8个热门AI模型,什么GPT4、Claude3最新模型,都能免费试用14天,我们只需要任意邮箱注册账号,然后下载程序即可。
具体用法
下载程序
进入Cursor官网,在右上角点击下载并安装
登陆授权
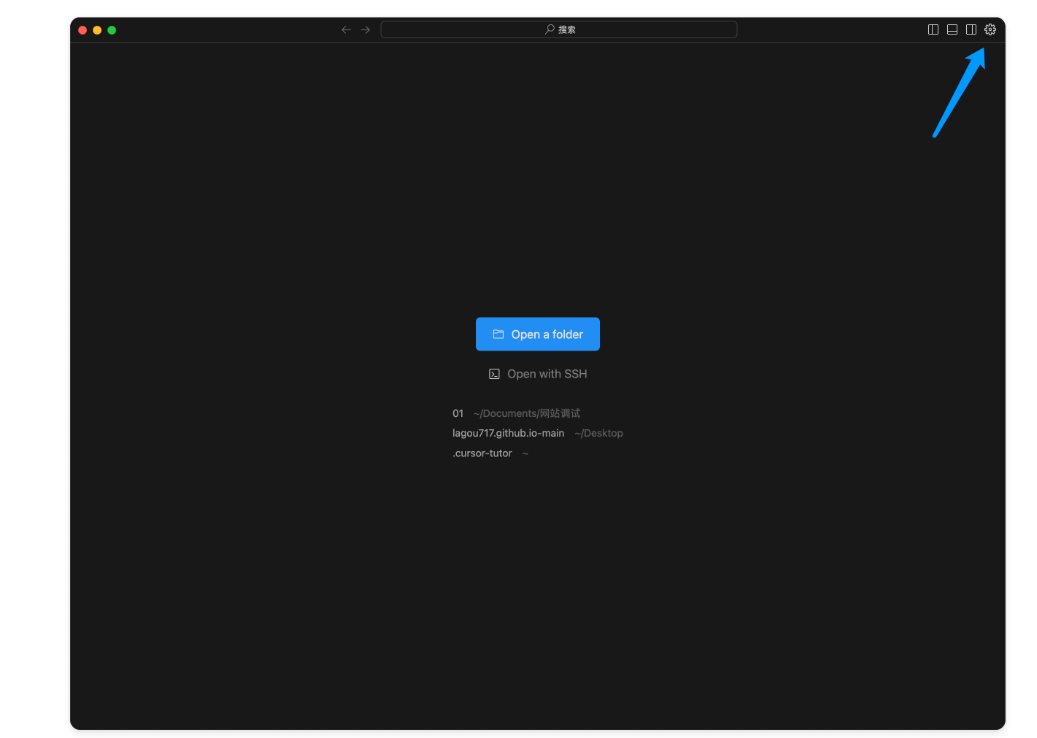
安装后打开软件,点击右上角的设置按钮
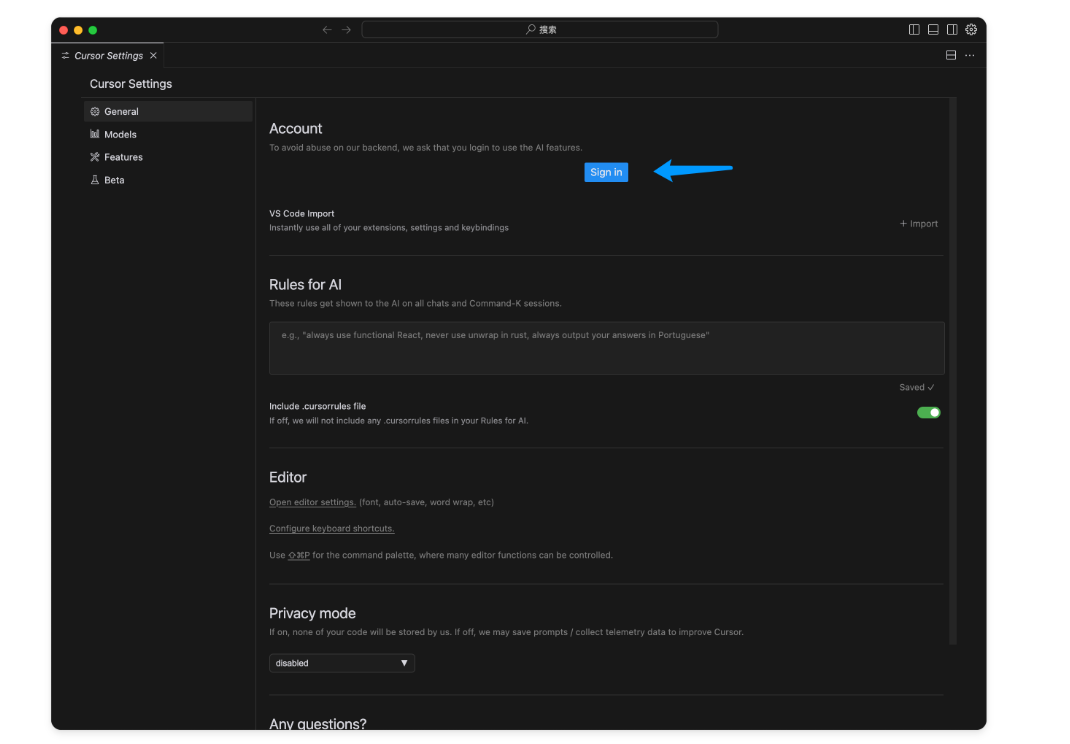
然后点击登陆,不出意外应该会弹出授权窗口
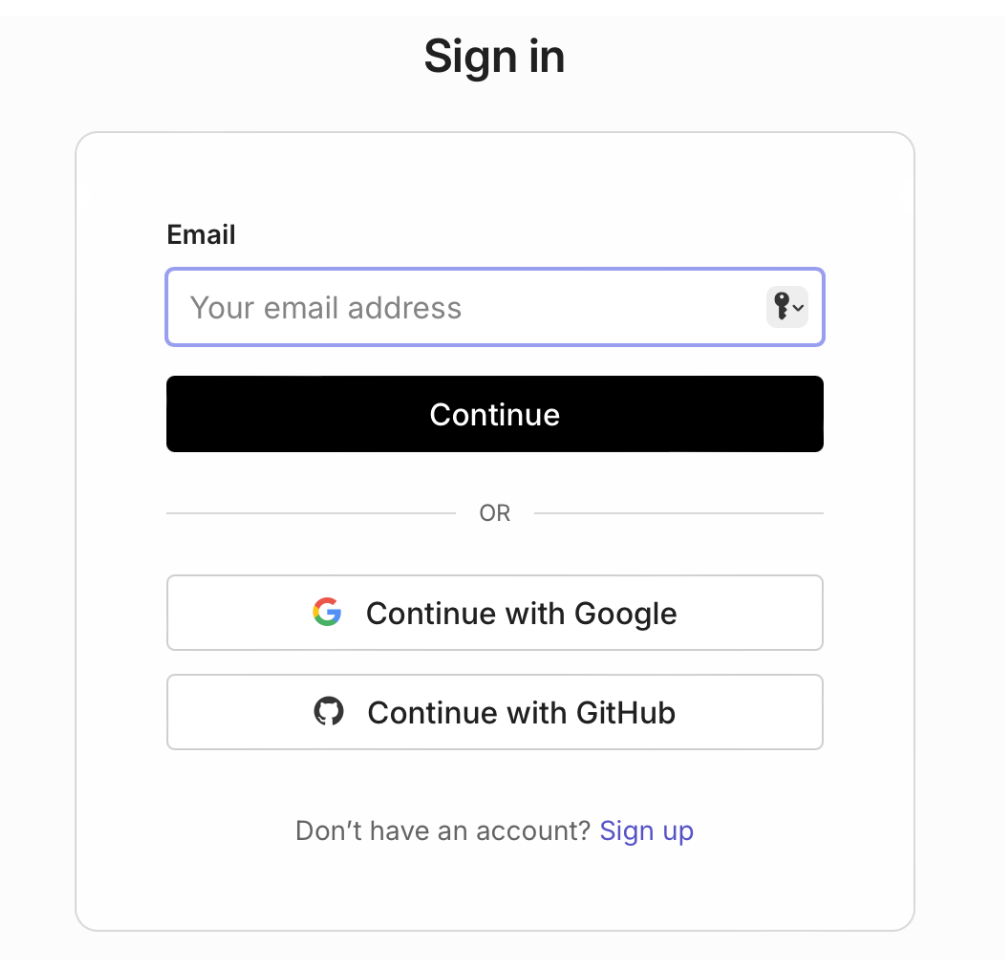
可以选择用GitHub或Google账号进行登陆,也可以直接点击注册,输入邮箱进行注册登陆,我这里以网易邮箱举例
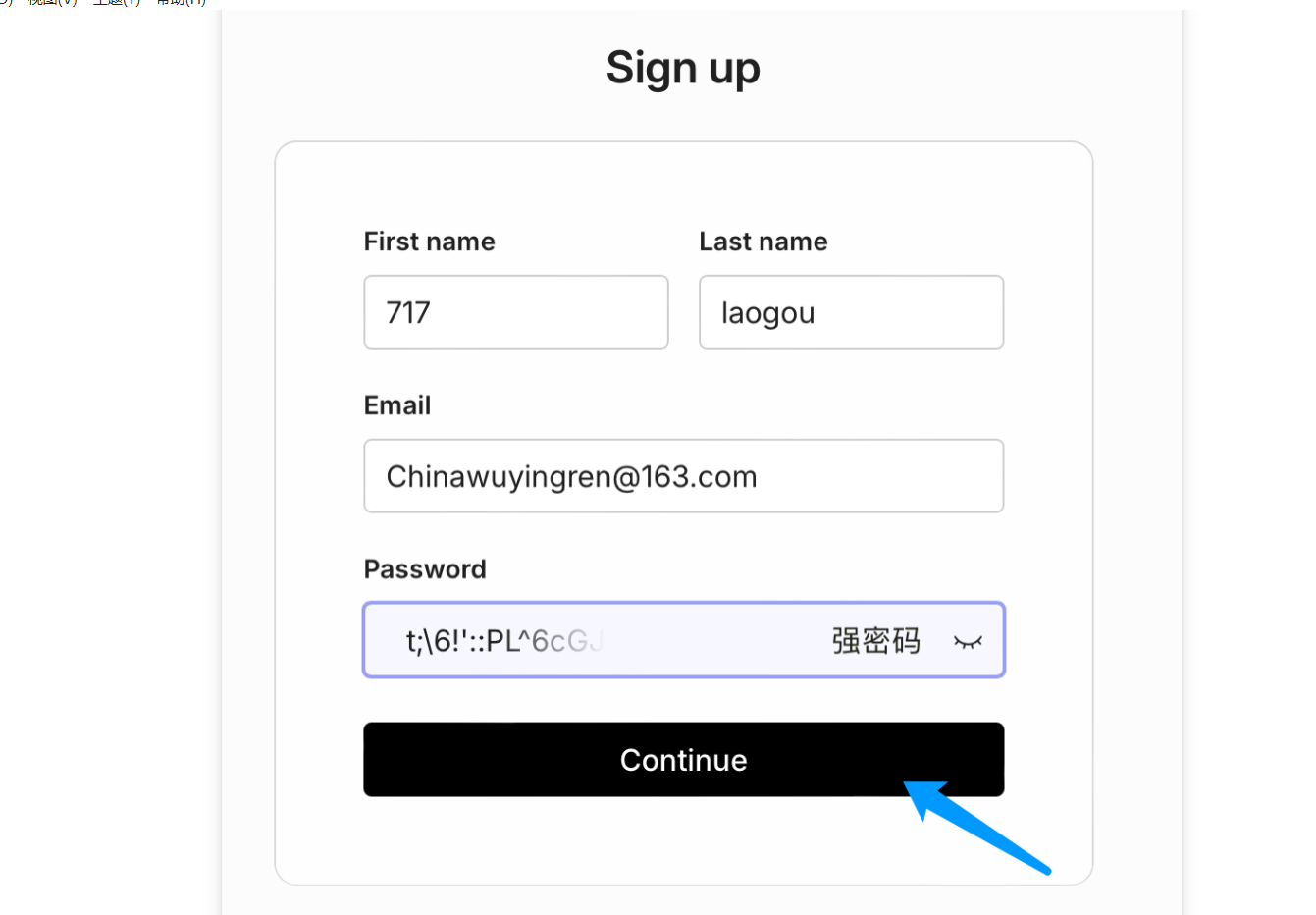
这里有概率提示验证失败,可以重试一般就会提示我们填入“邮箱验证码”
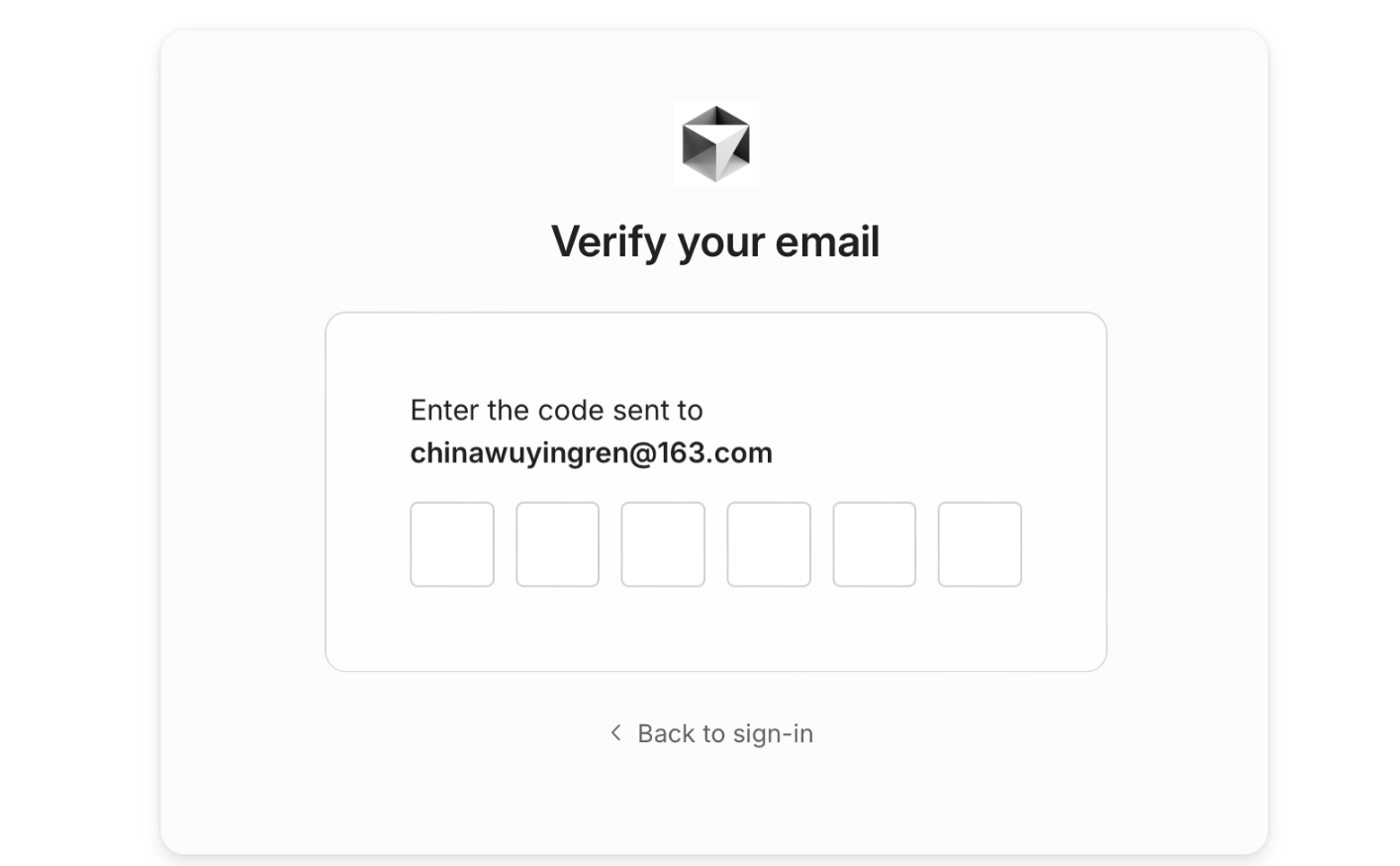
填入验证码进入下一步后,询问我们是否允许打开Cursor软件,这里点允许
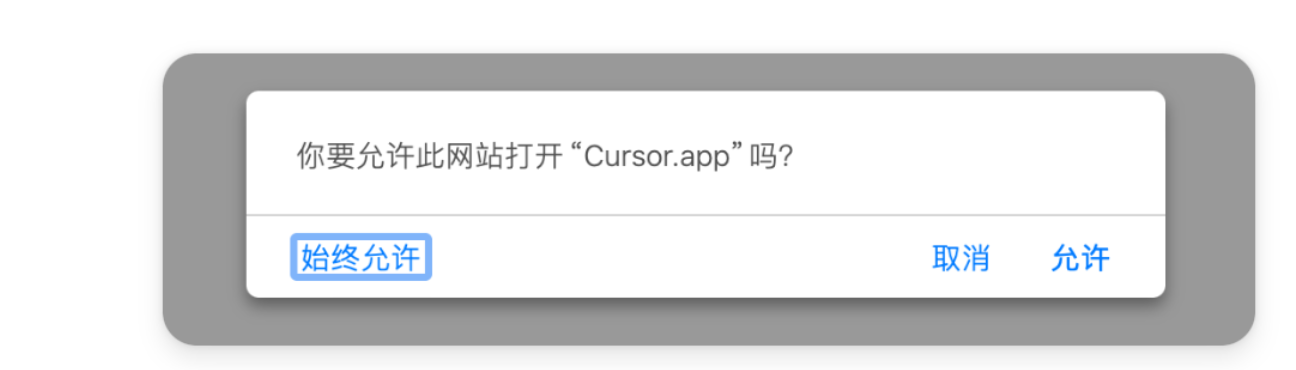
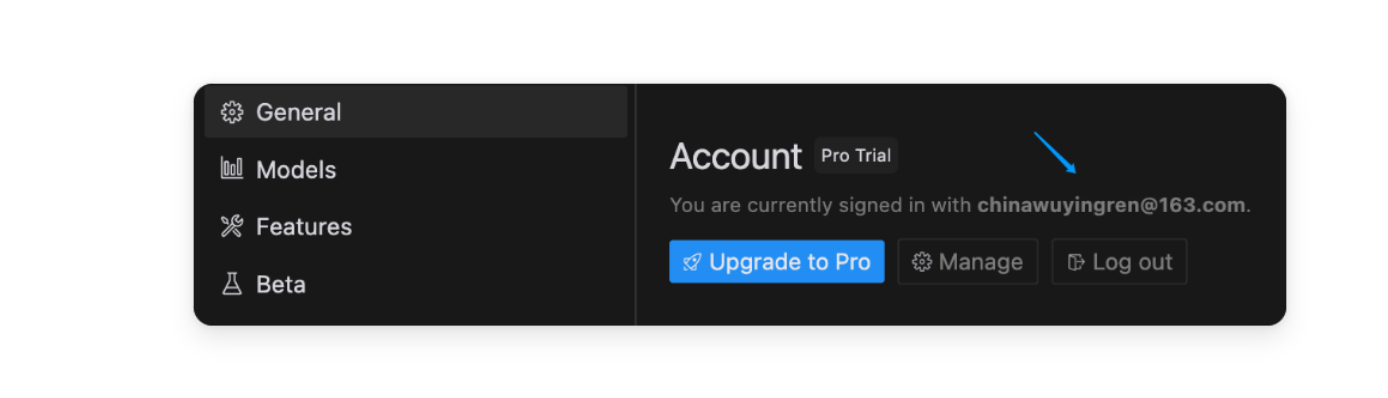
允许后就我们的软件后台就会显示这样的页面,如果没有显示就重新再点一次登陆进行重新授权
查看支持的模型
点击左侧的Models,可以看到支持的模型,勾选的模型就是我们可以使用的模型
[
如何使用
点击右上角的分屏图标
[
这时我们看到了一个分屏窗口,在这里可以直接与AI进行沟通
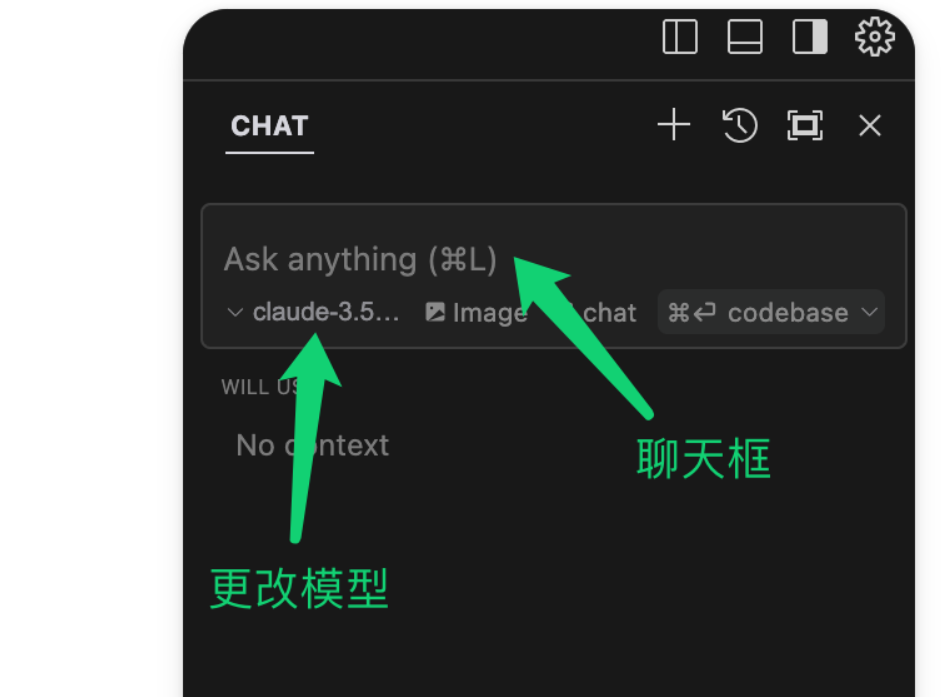
引用
-
Cursor官网
-
laogou717.com
这篇关于不容错过!最简单的Cursor无限注册攻略!的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





