本文主要是介绍2014.3树形动规练习2,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1、 树的重量
| 源程序名 weight.???(pas, c, cpp) 可执行文件名 weight.exe 输入文件名 weight.in 输出文件名 weight.out |
【问题描述】
树可以用来表示物种之间的进化关系。一棵“进化树”是一个带边权的树,其叶节点表示一个物种,两个叶节点之间的距离表示两个物种的差异。现在,一个重要的问题是,根据物种之间的距离,重构相应的“进化树”。
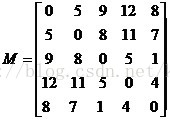
令N={1..n},用一个N上的矩阵M来定义树T。其中,矩阵M满足:对于任意的i,j,k,有M[i,j]+M[j,k]<=M[i,k]。树T满足:
1.叶节点属于集合N;
2.边权均为非负整数;
3.dT(i,j)=M[i,j],其中dT(i,j)表示树上i到j的最短路径长度。
如下图,矩阵M描述了一棵树。
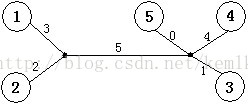
树的重量是指树上所有边权之和。对于任意给出的合法矩阵M,它所能表示树的重量是惟一确定的,不可能找到两棵不同重量的树,它们都符合矩阵M。你的任务就是,根据给出的矩阵M,计算M所表示树的重量。下图是上面给出的矩阵M所能表示的一棵树,这棵树的总重量为15。
【输入】
输入数据包含若干组数据。每组数据的第一行是一个整数n(2<n<30)。其后n-l行,给出的是矩阵M的一个上三角(不包含对角线),矩阵中所有元素是不超过100的非负整数 。输入数据保证合法。
输入数据以n=0结尾。
【输出】
对于每组输入,输出一行,一个整数,表示树的重量。
【样例】
weight.in weight.out
5 15
59 12 8 71
811 7
51
4
4
1536 60
3155
36
0
【题解】
【知识准备】
树的基本特征。
【算法分析】
本题是一道涉及树性质的算法题,所以我们应该以树的性质为突破口,来讨论本题的算法。
首先来看一下简单的实例,就以题目中给出的例子来说明。下图所示的树,有5个叶子节点,两个内点,6条边。我们已知的信息是任意两个叶子节点之间的距离,所以我们讨论的必然是叶子节点之间的关系,不可能涉及内点。
从图中我们可以看出,有些叶子结点是连在同一个内点上的,如①和②;也有些连在不同的内点上,如①和④。我们来看连在同一内点上的叶子节点有什么特殊的性质。就以①和②为例,①到③、④、⑤的距离分别为9、12、8,②到③、④、⑤的距离分别为8、11、7,正好都相差l。这个“1”差在哪里呢?①连到内点的边长为3,②连到内点的边长为2,两者相差为1。所以,相差的“1”正好就是两节点连到内点上的边长的差。再看①到②的距离,由于两叶子节点都是连在同一个内点上的,所以他们之间的距离,就是两者到内点的边长和。知道的边长和以及边长差,求出两边长就不难做到了。(注意:两叶子节点连到内点的边长是未知的)
再看一下不连在同一内点上的节点,①和④。①到②、③、⑤的距离分别为5、9、8,④到②、③、⑤的距离分别为11、5、4,没有一个统一的“差”。
其实,前面的结论都是非常直观而显然的,只不过关键是如何去利用。我们先来总结一下前面的结论:
(1)如果两叶子节点连在同一个内点上,则它们到其他叶子节点的距离有一个统一的“差”;
(2)如果两叶子节点连在不同的内点上,则它们到其他叶子节点的距离没有一个统一的“差”;
○
/
○────●────●
a \
○
值得注意的是,图6-3中的a点不能算内点。我们所指的内点是至少连接两个叶子节点的点,像a这样的点完全可以去掉,不会影响树的权值和,如下图。
○
/
○─────────●
\
○
(3)如果两叶子节点连在同一个内点上,则它们之间的距离等于它们各自到内点的边长的和。
根据(1)和(2)两条性质,很容易得到判断连接相同内点的两个叶子节点的方法,即必须满足它们到其他所有叶子节点有统一的距离差(充分且必要)。
找到两个连接相同内点的叶子节点并计算出它们各自到内点的边长(不妨设为l1和l2)以后,我们可以作这样的操作:删去一个节点,令另一个节点到内点的边长为l1+l2。这样得到的新树,权值和与原树相同,但叶子节点少了一个,如下图。
反复利用上述操作,最后会得到一棵只有两个叶子节点的树,这两个节点之间的边长就是原树的权值和。
算法需要反复执行n-2次删除节点的操作。每次操作中,需要枚举两个叶子节点,并且还要有一个一维的判断,时间复杂度是O(n3)的。所以,整个算法的时间复杂度是O(n4)的。对于一个规模仅有30的题目来说,O(n4)的算法足以解决问题了。当然,算法本身应该还是有改进的余地的,不过这里就不加以讨论了。
【代码】
#include<cstdio>int deleted[31];
int del,n,map[31][31];bool check(int x,int y)
{del=0; bool mark=true; //不能用DEL=某个数 代替MARK 会出错 for (int a=1;a<=n;a++)if (a!=x && a!=y && deleted[a] ) {if (mark) { del=map[x][a]-map[y][a]; mark=false; }else if (del!=map[x][a]-map[y][a]) return 0;}return 1;
}void merge(int x,int y)
{deleted[y]=0;int ty=(map[x][y]-del)>>1; //计算删去一条边权值for (int i=1;i<=n;i++) if (deleted[i]) { map[x][i]+=ty; map[i][x]+=ty; } //增加距离,相当于点合成} void work( ){for (int i=1;i<=n;i++)for (int j=1;j<=n;j++)if (i!=j && deleted[i] && deleted[j] ) if (check(i,j)){ merge(i,j);return;}
}int main()
{freopen("weight.in","r",stdin);freopen("weight.out","w",stdout);while ( scanf("%d",&n) && n) { for (int i=1;i<n;i++) {deleted[i]=1;for (int j=i+1;j<=n;j++) { scanf("%d",&map[i][j]); map[j][i]=map[i][j]; }}deleted[n]=1;for (int i=1;i<=n-2;i++) work(); //一共进行N-2次int n1,n2;for (n1=1;n1<=n;n1++) if (deleted[n1]) break;for (n2=n1+1;n2<=n;n2++) if (deleted[n2]) break;printf("%d\n",map[n1][n2]);}
} 这篇关于2014.3树形动规练习2的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!