本文主要是介绍贪婪大陆(线段树题解),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
P2184 贪婪大陆
用线段树维护一个区间的sum和tag(懒标记)
我的第一打,没用上容斥原理
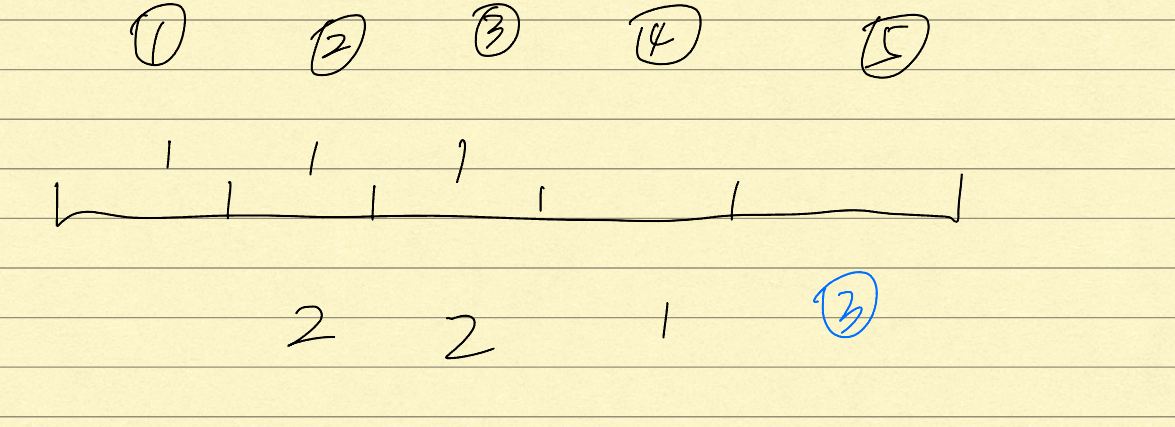
显然如果第五个区间也加入第三种,我们再访问3-5有多少种用我下面的代码只能是2种
#include<bits/stdc++.h>using namespace std;
typedef long long ll;
const int N=1e5+10;
#define ls (u<<1)
#define rs (u<<1|1)
#define mid (l+r>>1)
int L,R;struct Node
{ll maxn[N<<2];ll add[N<<2];ll sum[N<<2];void pushup(int u){maxn[u]=max(maxn[ls],maxn[rs]);}void pushdown(int u,int l,int r){if(add[u]){maxn[ls]=max(maxn[ls],maxn[ls]+add[u]);maxn[rs]=max(maxn[rs],maxn[rs]+add[u]);add[ls]+=add[u];add[rs]+=add[u];add[u]=0;}}void modify(int u,int l,int r){if(L<=l&&r<=R){maxn[u]+=1;add[u]+=1;return ;}pushdown(u,l,r);if(L<=mid) modify(ls,l,mid);if(R>mid) modify(rs,mid+1,r);pushup(u);}ll query(int u,int l,int r){if(L<=l&&r<=R) return maxn[u];pushdown(u,l,r);ll res=0;if(L<=mid) res=max(res,query(ls,l,mid));if(R>mid) res=max(res,query(rs,mid+1,r));return res;}}tr[1];signed main()
{int n,m;cin>>n>>m;//tr[0].build(1,1,n);int op;while(m--){cin>>op>>L>>R;if(op==1) tr[0].modify(1,1,n);else cout<<tr[0].query(1,1,n)<<endl;}return 0;
}
关于二维差分的理解,我好像一直都有问题
今天看了这篇讲解懂了,之前一直把二维差分和一维差分搞混,二维差分实际是用于求子矩阵的,而不是说从 a [ i ] [ j ] a[i][j] a[i][j]一直到 a [ 0 ] [ 0 ] a[0][0] a[0][0]的所有坐标点所代表的y值的和,那这样为什么不直接用一维矩阵去存差分,我真的,两年了,才懂😂
那其实贪婪大陆这道题更像是一维差分+线段树
“R之前的所有区间开头数(包括R)-L之前的所有区间结尾数(不包括L)”
仔细在脑中想一想这句话,会发现:记录 1 − r 1-r 1−r中的所有开头,减去 1 − l − 1 1-l-1 1−l−1中的所有结尾就是 l − r l-r l−r中的所有种类数目
放在线段树里维护什么呢
可以维护开头和结尾,用公式一减就是答案了,单点查询(变相的区间查询)
考察线段树查找不同种类的区间的个数,下次如果碰到了这类型的题目可以用上面的思想
这篇题解的图更加好理解
#include<bits/stdc++.h>using namespace std;
typedef long long ll;
const int N=1e5+10;
#define ls (u<<1)
#define rs (u<<1|1)
#define mid (l+r>>1)
int L,R;
int x;struct Node
{ll sum[N<<2];ll hl[N<<2]; //在l左边结尾ll hr[N<<2]; //在r左边开头void pushup(int u,int op){if(op==1) hl[u]=hl[ls]+hl[rs];else hr[u]=hr[ls]+hr[rs];}void pushdown(int u,int l,int r){if(hr[u]){hr[ls]+=hr[u];hr[rs]+=hr[u];hr[u]=0;}if(hl[u]){hl[ls]+=hl[u];hl[rs]+=hl[u];hl[u]=0;}}void modify(int u,int l,int r,int op){if(l==x&&r==x){if(op==1) hl[u]+=1;else hr[u]+=1;return ;}//不用懒标记,因为单点修改就是对叶子节点的修改了//只用统计区间和即可//pushdown(u,l,r);if(x<=mid) modify(ls,l,mid,op);if(x>mid) modify(rs,mid+1,r,op);pushup(u,op);}ll query(int u,int l,int r,int op){if(L<=l&&r<=R){if(op==1) return hl[u];else return hr[u];}//pushdown(u,l,r);ll res=0;if(L<=mid) res+=query(ls,l,mid,op);if(R>mid) res+=query(rs,mid+1,r,op);return res;}}tr[1];signed main()
{int n,m;cin>>n>>m;//tr[0].build(1,1,n);int op;while(m--){cin>>op>>L>>R;if(op==1){//一定要牢记hr和hl的定义分别是开头的个数,结尾的个数x=L;tr[0].modify(1,1,n,2);x=R;tr[0].modify(1,1,n,1);}else{int a=L,b=R;L=1,R=a-1;ll resl=tr[0].query(1,1,n,1);R=b;ll resr=tr[0].query(1,1,n,2);cout<<resr-resl<<endl;//cout<<resr<<endl;//cout<<resl<<endl;}}return 0;
}
这篇关于贪婪大陆(线段树题解)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!