【数据结构与算法】深入理解归并排序（Merge Sort）

本文主要是介绍【数据结构与算法】深入理解归并排序（Merge Sort），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

问题背景与引入

排序问题是计算机科学中的基础问题之一，几乎在所有的数据处理过程中都会遇到。例如，在数据库查询中，我们通常需要按某个字段对数据进行排序，以便快速检索。在图形处理和数据分析中，排序也是一项关键操作。

归并排序（Merge Sort）是计算机科学中最经典的排序算法之一，它以其稳定的时间复杂度和良好的排序性能在各种应用场景中得到广泛应用。

归并排序的算法原理

归并排序是一种基于“分治法”的排序算法。分治法是一种递归分解问题、解决子问题并将其合并的策略。归并排序正是通过递归地将一个序列分割成若干子序列，将每个子序列排序后再将其合并，从而达到对整个序列排序的目的。

分割阶段

在分割阶段，归并排序通过递归地将待排序序列从中间分成两部分，直到每个子序列只有一个元素或为空。对于一个长度为 n 的序列，这个分割过程大约会进行 log₂(n) 次。

合并阶段

在合并阶段，归并排序将之前分割出的子序列逐一合并。每次合并时，两个有序的子序列通过比较元素大小，依次合并成一个新的有序序列。

示例

我们用一个简单的例子来说明这个过程

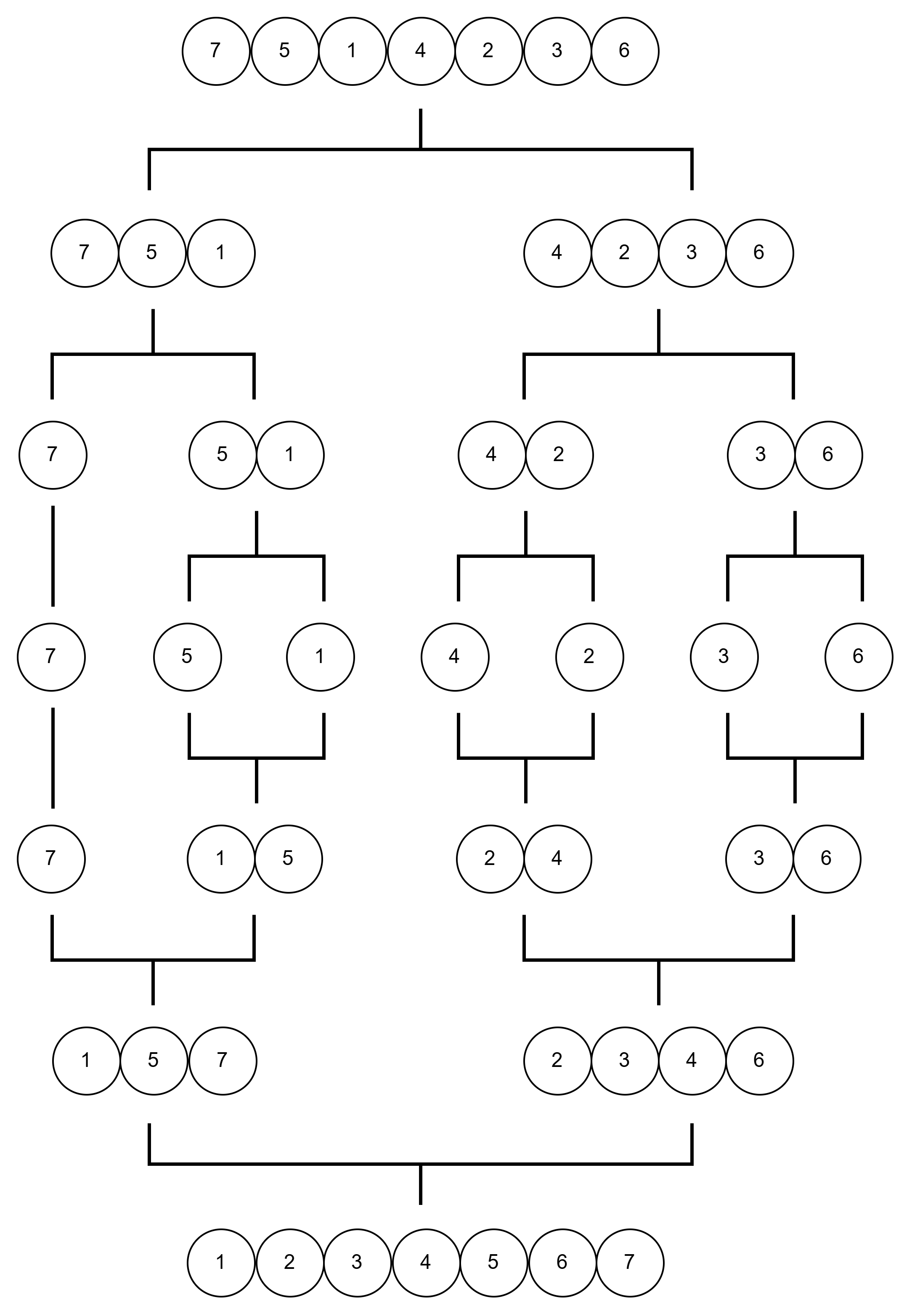
如上图，我们先将完整的序列划分到不能再分为止，即子序列长度为1

然后将其合并，合并时的操作是将两个有序序列合并成一个新的有序序列。合并后的新序列与另一个新序列合并，直到得到最终排序结果

在这个过程中，最主要的操作就是将两个有序序列合并成一个有序序列，这个操作其实是很简单的，我们只需要比较两个元素大小，将较小的元素插入到新数组中，然后继续比较下一个元素，直到其中一个数组被完全遍历，然后将另一个数组剩余的元素插入到新数组中。

归并排序的实现细节

以下是我实现的一个归并排序的 Python 代码：

def mergesort(arr, i, j):"""使用归并排序算法对数组进行排序。参数:arr -- 待排序的数组i -- 排序的起始索引j -- 排序的结束索引"""# 当数组只有一个元素时，不需要排序if j - i == 1:return# 计算中间索引，将数组分成两半mid = (i + j) // 2# 递归调用mergesort，对左半部分进行排序mergesort(arr, i, mid)# 递归调用mergesort，对右半部分进行排序mergesort(arr, mid, j)# 将排序好的左右两部分合并arr[i:j] = merge(arr[i:mid], arr[mid:j])def merge(arr1, arr2):"""将两个已排序的数组合并为一个排序的数组。参数:arr1 -- 第一个已排序数组arr2 -- 第二个已排序数组返回:合并后的排序数组"""# 初始化一个新的数组用于存储合并后的排序数组arr = []# 初始化第二个数组的索引j = 0# 遍历第一个数组for i in range(len(arr1)):# 当第二个数组还有元素且其元素小于第一个数组当前元素时，将第二个数组的元素添加到新数组中while j < len(arr2) and arr1[i] > arr2[j]:arr.append(arr2[j])j += 1# 否则，将第一个数组当前元素添加到新数组中else:arr.append(arr1[i])else:# 将第二个数组剩余的元素添加到新数组中arr.extend(arr2[j:])# 返回合并后的排序数组return arr

代码解析

1. mergesort 函数首先判断数组是否已经不能再分割（即长度小于等于 1），如果是，直接返回。

2. 否则，将数组分为左右两部分，分别递归调用 mergesort 进行排序。

3. 排序后的两个子数组通过 merge 函数合并成一个有序数组。

   merge 函数是合并两个有序数组的关键部分。它通过两个指针 i 和 j 分别遍历 arr1 和 arr2 数组，并将较小的元素插入到结果数组 arr 中。最后，将剩余未处理的元素直接添加到 arr 中。

运行示例

这里给出一个测试用例确认排序结果是否正确

arr = [38, 27, 43, 3, 9, 82, 10]
mergesort(arr, 0, len(arr))
print(arr)

运行结果为：

[3, 9, 10, 27, 38, 43, 82]

复杂度分析

时间复杂度

归并排序的时间复杂度为 O(n log n)，其中 n 是数组的长度，log n 是由于分割数组的递归层数。在每一层递归中，合并操作的时间复杂度为 O(n)，因此总体时间复杂度为 O(n log n)。

这种复杂度在所有情况下（最坏、最好、平均）都是相同的，这使得归并排序在处理大型数据集时表现非常稳定。

我们可以与最简单的冒泡排序还有内置的timsort排序进行一个对比

def bubble_sort(arr):for i in range(len(arr)):for j in range(len(arr) - i - 1):if arr[j] > arr[j + 1]:arr[j], arr[j + 1] = arr[j + 1], arr[j]arr = [random.randint(-9999, 9999) for _ in range(10000)]
arr1 = arr.copy()
arr2 = arr.copy()
arr3 = arr.copy()
print('归并排序')
t = time.time()
mergesort(arr1, 0, len(arr1))
print(time.time() - t)
print('冒泡排序')
t = time.time()
bubble_sort(arr2)
print(time.time() - t)
print('内置排序')
t = time.time()
arr3.sort()
print(time.time() - t)print(f'正确性检验arr1==arr2==arr3:{arr1 == arr2 == arr3}')

运行结果如下

归并排序
0.016516447067260742
冒泡排序
4.049731254577637
内置排序
0.0010013580322265625
正确性检验arr1==arr2==arr3:True

可以很直观的看到，归并排序的速度要远快于冒泡排序。当然，跟内置的timsort排序相比，归并排序还是要慢许多

空间复杂度

归并排序的空间复杂度为 O(n)。这是因为在合并两个子序列时，需要额外的存储空间来保存中间结果。这也是归并排序的一个主要缺点，相比于一些就地排序算法，如快速排序，它需要更多的内存。

归并排序的优缺点

优点

1. 稳定性：归并排序是稳定排序算法，即相同元素在排序后的相对顺序保持不变。这对于某些应用场景非常重要，如在多关键字排序中。

2. 性能稳定：归并排序在最坏情况下的时间复杂度为 O(n log n)，这使得它在处理各种情况下表现都很出色，尤其是在处理大规模数据时。

3. 适合外部排序：由于归并排序的分割和合并特性，它可以很好地用于外部排序，即当数据量大到无法全部加载到内存时，归并排序可以与磁盘存储相结合进行排序。

缺点

1. 空间复杂度较高：由于需要额外的存储空间来保存合并结果，归并排序在空间使用上不如一些原地排序算法（如快速排序）高效。

2. 较高的常数因素：尽管归并排序的时间复杂度为 O(n log n)，与快速排序相同，但其递归结构和额外的合并操作使得其实际运行时间往往比快速排序稍长，尤其是在处理小规模数据时。

归并排序的应用场景

归并排序因其稳定性和良好的性能，适用于许多实际应用场景：

1. 大规模数据排序：当数据集非常庞大时，归并排序的 O(n log n) 时间复杂度使其非常适合。

2. 外部排序：在处理超过内存容量的数据集时，归并排序可以与外部存储（如磁盘）结合使用，进行高效排序。

3. 合并有序文件：归并排序的合并过程可以直接应用于将多个有序文件合并为一个有序文件

结语

归并排序是一种经典且强大的排序算法，通过分治策略和递归实现，能够在各种情况下提供稳定的性能表现。尽管它在空间使用上存在不足，但其稳定性和适应大规模数据的能力使其在许多应用场景中占据重要地位。

这篇关于【数据结构与算法】深入理解归并排序（Merge Sort）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---