本文主要是介绍【数学建模】层次分析法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
在数学建模问题求解中什么时候用到层次分析法
在数学建模问题求解中,层次分析法(Analytic Hierarchy Process, AHP)通常用于解决评价类问题,特别是在需要从多个备选方案中选择最佳方案时。以下是一些典型的应用场景:
- 方案选择:
-
- 当需要从多个备选方案中选择最佳方案时,可以使用层次分析法。例如,在选择最佳旅游目的地时,需要根据不同的评价指标(如景色、花费、居住条件等)来评估备选方案(如苏杭、北戴河、桂林)。
- 资源分配:
-
- 当需要根据不同的评价标准来分配有限资源时,可以使用层次分析法。例如,高校奖学金的分配、项目资金的分配等。
- 决策支持:
-
- 当决策者需要在多个维度上评估和比较不同的选项时,层次分析法可以作为一种决策支持工具。例如,在选择最佳投资项目时,需要综合考虑投资回报率、风险、市场潜力等多个因素。
- 质量评估:
-
- 当需要评估产品的质量或服务的水平时,可以使用层次分析法。例如,评估不同型号汽车的安全性、燃油经济性、舒适性等。
- 优先级排序:
-
- 当需要确定任务或项目的优先级时,层次分析法可以帮助确定各项任务的重要程度。例如,在项目管理中,确定不同任务的优先级。
应用实例
选择最佳旅游目的地
- 目标:为小明同学选择最佳的旅游景点。
- 备选方案:苏杭、北戴河、桂林。
- 评价指标:景色、花费、居住、饮食、交通。
步骤详解
- 构建层次结构:
-
- 目标层:选择最佳旅游地。
- 准则层:景色、花费、居住、饮食、交通。
- 方案层:苏杭、北戴河、桂林。
- 构造判断矩阵:
-
- 对于目标层与准则层的判断矩阵,需要比较景色、花费、居住、饮食和交通之间的相对重要性。
- 对于准则层与方案层的判断矩阵,需要比较苏杭、北戴河和桂林之间的相对重要性。
- 计算权重:
-
- 使用算术平均法、几何平均法或特征值法计算每个准则或方案的权重。
- 例如,特征值法计算出的权重矩阵如下:
||指标权重|苏杭|北戴河|桂林|
|-|-|-|-|-|
|景色|0.2636|0.5954|0.2764|0.1283|
|花费|0.4758|0.0819|0.2363|0.6817|
|居住|0.0538|0.4286|0.4286|0.1429|
|饮食|0.0981|0.6337|0.1919|0.1744|
|交通|0.1087|0.1667|0.1667|0.6667|- 一致性检验:
-
- 计算一致性指标CI和一致性比率CR。
- 如果CR小于0.1,则认为判断矩阵的一致性可以接受。
- 计算综合得分:
-
- 根据权重矩阵计算得分,并进行排序。
- 例如,最终计算出的得分如下:
-
-
- 苏杭得分:0.299
- 北戴河得分:0.245
- 桂林得分:0.455
-
- 决策:
-
- 根据综合得分,桂林是最佳的旅游目的地。
注意事项
- 数据来源:确保评价指标的数据来源可靠且全面。
- 专家意见:在构造判断矩阵时,可以参考专家的意见或行业标准。
- 一致性检验:确保判断矩阵的一致性,以提高决策的准确性。
- 多方法验证:使用多种方法计算权重,以增加结果的稳健性。
通过以上步骤,层次分析法可以有效地应用于评价类问题的解决,帮助决策者在复杂多变的环境中做出合理的选择。
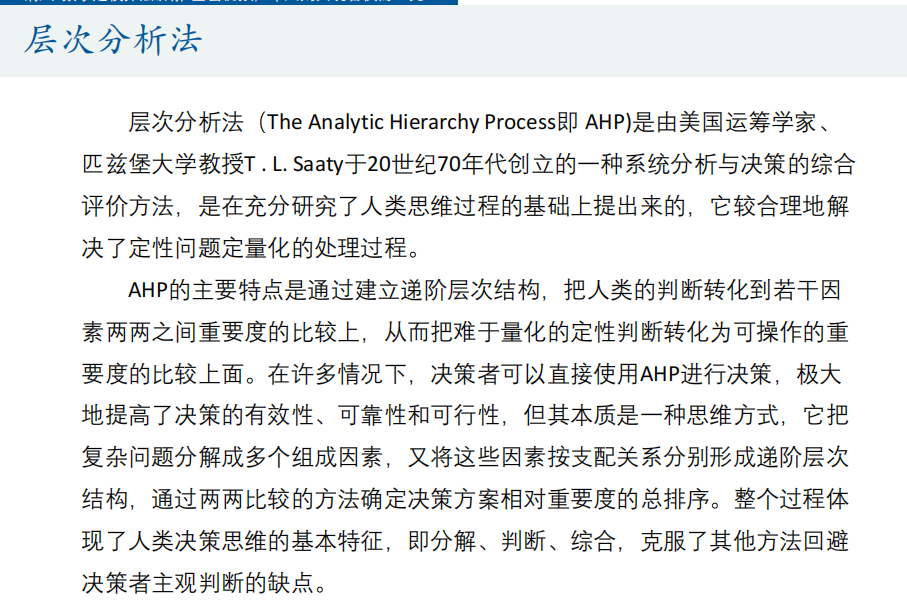
在视频课程的第一讲中,层次分析法(Analytic Hierarchy Process, AHP)被介绍为一种解决评价类问题的有效方法。这种方法由美国运筹学家T.L. Saaty教授在20世纪70年代提出,主要用于帮助决策者在面对多标准决策问题时做出合理的选择。
主要分析思路概括如下:
- 问题背景:
-
- 使用层次分析法解决的问题通常涉及多种选择方案及多个评价标准。
- 例如,视频中举了一个例子,即高考结束后学生需要选择大学(华科或武大),以及另一个例子,即选择最佳旅游地点(苏杭、北戴河或桂林)。
- 基本步骤:
-
- 确定目标:明确决策的目标是什么。
- 识别备选方案:列出所有可能的选择方案。
- 确定评价指标:基于问题背景,确定评价各个方案的标准或准则。
-
-
- 例如,选择大学时的指标可能是学习氛围、就业前景、男女比例和校园景色等。
- 选择旅游地点时的指标可能是景色、花费、居住、饮食和交通等。
-
- 构建层次结构:
-
- 建立一个层次结构图,将目标、评价指标和备选方案组织起来。
-
-
- 目标层(最高层):决策目标。
- 准则层(中间层):评价指标。
- 方案层(最低层):备选方案。
-
- 构造判断矩阵:
-
- 对于同一层次的元素,按照其相对于上一层某个准则的重要性,进行两两比较。
- 判断矩阵中元素的值表示两个因素相比的重要程度,一般采用1-9标度。
- 计算权重:
-
- 通过判断矩阵计算出每个指标的权重,可以采用算术平均法、几何平均法或特征值法。
- 例如,对于选择旅游地点的例子,给出了不同指标下的权重矩阵。
- 方案得分计算:
-
- 根据权重矩阵和备选方案在各个指标下的得分,计算每个方案的总得分。
- 最终得分最高的方案被视为最优选择。
- 决策:
-
- 根据计算得出的总得分,选出最佳方案。
- 注意事项:
-
- 在确定指标权重时,避免直接询问决策者对所有指标的权重,因为这样可能导致考虑不周全。
- 使用层次分析法时,应该注意确保判断的一致性,以提高决策的可靠性。
通过这样的步骤,层次分析法能够帮助人们在复杂的多标准决策问题中,系统化地评估各个选项并作出合理的选择。
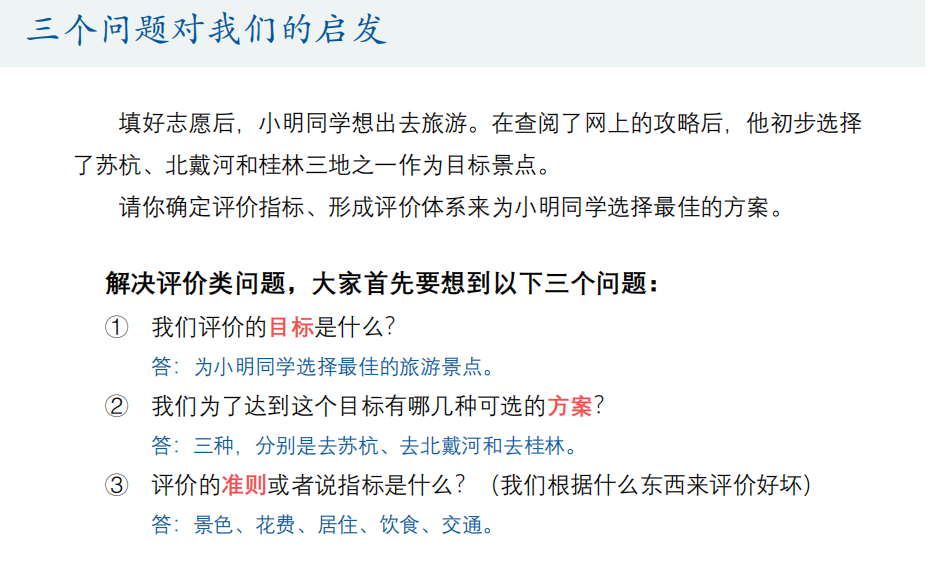
问题背景如下:
小明已经完成了高考志愿的填报,现在他计划出去旅游放松一下。在浏览了网上的旅游攻略之后,他初步选定了三个旅游目的地:苏杭、北戴河和桂林。为了确定哪个地方最适合他,需要建立一个评价体系,对这三个地点进行评估。
首先,需要解决三个核心问题:
- 评价的目标是什么?
-
- 答:为小明选择最佳的旅游景点。
- 为了达到这个目标有哪些可选方案?
-
- 答:三个方案,分别是去苏杭、去北戴河和去桂林。
- 评价的准则或者说指标是什么?
-
- 答:题目没有提供具体的指标数据,需要我们来确定。
为了确定评价指标,可以通过以下途径:
- 优先在学术数据库如知网、万方、百度学术、谷歌学术等平台搜索相关文献,这样显得更为专业,也可以借鉴别人的研究方法。
- 如果找不到相关文献,可以组织小组讨论,或者在网络上搜索专家的意见。
- 推荐使用虫部落-快搜网站来搜索信息,如果在国内无法访问谷歌,可以使用百度搜索。
- 搜索的关键字可以包括:“旅游选择因素”、“根据什么因素选择旅游景点”、“旅游景点评价指标”等。
假设经过资料搜集,选择了以下五个评价指标:
- 景点景色
- 旅游花费
- 居住环境
- 饮食情况
- 交通便利程度
接下来,需要通过层次分析法来确定这些指标的权重,并据此为每个旅游目的地评分,从而帮助小明做出最佳选择。层次分析法的步骤包括:
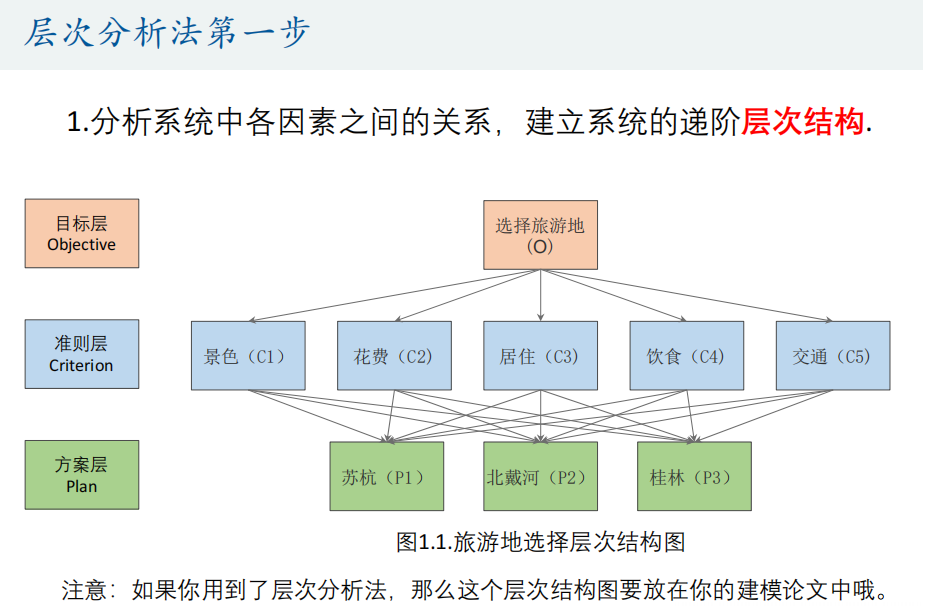
- 分析系统中各因素之间的关系,建立系统的递阶层次结构。
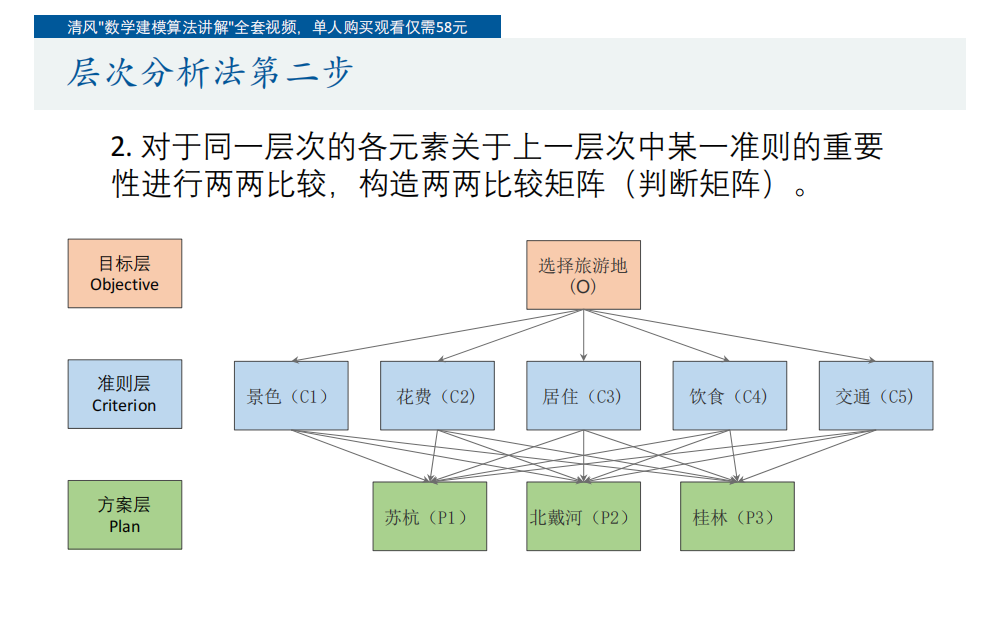
- 构造两两比较矩阵(判断矩阵)。
- 计算被比较元素对于该准则的相对权重,并进行一致性检验。
- 根据权重矩阵计算得分,并进行排序。
最终目的是根据以上指标和权重,为每个旅游地点打分,选出最适合小明的目的地。
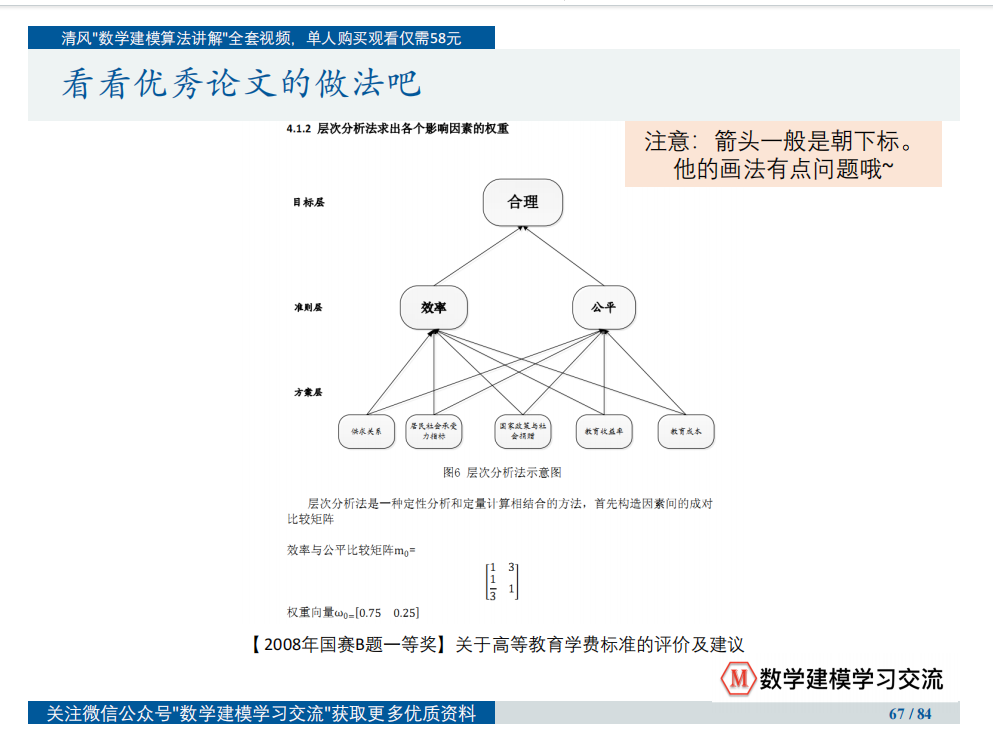
层次分析法的基本步骤
层次分析法(Analytic Hierarchy Process, AHP)是一种常用的多准则决策分析工具,它可以帮助我们在面临复杂决策问题时,系统地评估各种选项。以下是使用层次分析法的基本步骤:
- 构建层次结构:
-
- 目标层: 明确决策目标,例如选择最佳旅游目的地。
- 准则层: 确定评价标准或指标,比如景色、花费、居住、饮食和交通等。
- 方案层: 列出所有备选方案,如苏杭、北戴河、桂林等。
- 构造判断矩阵:
-
- 对于每一组相互比较的要素(如不同旅游地点的景色),构造一个判断矩阵。
- 矩阵中的元素代表两个要素之间相对重要性的标度,标度范围通常为1至9,其中1表示两者同等重要,9表示一个要素极端重要。
- 例如,在比较苏杭、北戴河和桂林的景色时,苏杭与北戴河相比的标度为2,表示苏杭的景色比北戴河稍微重要一些。
- 计算权重:
-
- 使用算术平均法、几何平均法或特征值法来计算每个准则或方案的权重。
- 算术平均法是通过将判断矩阵按列归一化,然后按行求和并除以矩阵的阶数来计算权重。
- 几何平均法是通过计算每行元素的几何平均数,然后对结果进行归一化来得到权重。
- 特征值法是通过求解判断矩阵的最大特征值及其对应的特征向量,然后对特征向量进行归一化来得到权重。
- 一致性检验:
-
- 为了确保判断矩阵的合理性,需要进行一致性检验。
- 一致性检验通过计算一致性指标(CI)和一致性比率(CR)来进行。
- CI通过比较最大特征值与矩阵阶数的差值来衡量矩阵的一致性程度。
- RI是随机一致性指标,根据矩阵阶数的不同而变化。
- CR通过CI与RI的比值来计算,如果CR小于0.1,则认为判断矩阵的一致性是可以接受的。
- 计算综合权重:
-
- 根据准则层的权重和方案层的权重,计算出每个方案的综合权重。
- 决策:
-
- 根据综合权重,对备选方案进行排序,从而选择最佳方案。
举例来说,如果我们正在评估苏杭、北戴河和桂林作为旅游目的地的优劣,可以按照以下步骤操作:
- 构建层次结构:
-
- 目标层:选择最佳旅游目的地
- 准则层:景色、花费、居住、饮食、交通
- 方案层:苏杭、北戴河、桂林
- 构造判断矩阵:
-
- 比较苏杭、北戴河和桂林的景色,构造相应的判断矩阵。
- 计算权重:
-
- 使用算术平均法、几何平均法或特征值法计算出景色这一准则下,苏杭、北戴河和桂林的权重。
- 例如,使用算术平均法计算得出苏杭的权重为0.5949,北戴河的权重为0.2766,桂林的权重为0.1285。
- 一致性检验:
-
- 对景色的判断矩阵进行一致性检验,确保一致性比率CR小于0.1。
- 计算综合权重:
-
- 同样计算出花费、居住、饮食和交通的权重,并结合准则层的权重,计算出苏杭、北戴河和桂林的综合权重。
- 决策:
-
- 根据综合权重,选择综合评分最高的地点作为旅游目的地。
这样,层次分析法通过一系列的量化步骤帮助我们做出更加客观和合理的决策。构建层次结构是层次分析法(AHP)中的一个重要步骤,它帮助我们清晰地组织问题和解决方案。以下是构建层次结构的具体步骤:

构建层次结构的步骤
- 确定目标层:
-
- 明确决策的目标,也就是最终要解决的问题。
- 例如,在选择旅游目的地的情况下,目标就是为小明同学选择最佳的旅游景点。
- 识别准则层:
-
- 确定评价标准或准则,即根据哪些方面来评价备选方案。
- 例如,在旅游地选择中,准则可能包括景色、花费、居住条件、饮食质量和交通便利程度等。
- 列举方案层:
-
- 列出所有备选方案。
- 在这个例子中,备选方案为苏杭、北戴河和桂林。
- 绘制层次结构图:
-
- 使用图表的形式将上述层级结构可视化,以便于理解和沟通。
- 图表中,目标层位于顶部,准则层居中,方案层位于底部。
示例
旅游目的地选择层次结构
- 目标层:
-
- 选择最佳旅游地 (O)
- 准则层:
-
- 景色(C1)
- 花费(C2)
- 居住(C3)
- 饮食(C4)
- 交通(C5)
- 方案层:
-
- 苏杭(P1)
- 北戴河(P2)
- 桂林(P3)
层次结构图
使用图形工具,如Microsoft Office中的SmartArt、专业的绘图软件如亿图图示或Visio,甚至在线工具如ProcessOn,可以创建如下图所示的层次结构图:
选择最佳旅游地 (O)/ | \景色(C1) 花费(C2) 居住(C3)| | |
苏杭(P1) 北戴河(P2) 桂林(P3)或者更详细的结构图:
选择最佳旅游地 (O)/ \ \ \ \
景色(C1) 花费(C2) 居住(C3) 饮食(C4) 交通(C5)/ \ / \ / \ / \ / \
苏杭(P1) 北戴河(P2) 桂林(P3) 苏杭(P1) 北戴河(P2) 桂林(P3) 苏杭(P1) 北戴河(P2) 桂林(P3) 苏杭(P1) 北戴河(P2) 桂林(P3) 苏杭(P1) 北戴河(P2) 桂林(P3)使用工具创建层次结构图
- SmartArt:
-
- 在Microsoft Office中,可以选择SmartArt图形来快速创建层次结构图。
- 专业绘图软件:
-
- 使用亿图图示等专业绘图软件,通过简单的拖拽和编辑功能创建层次结构图。
- 创建步骤包括:新建组织结构图、绘制矩形、调整布局、添加文本和连接线等。
- 在线工具:
-
- 如果不想下载软件,可以使用在线工具如ProcessOn来绘制层次结构图。
注意事项
- 图示要求:
-
- 如果你在建模论文中使用了层次分析法,记得将层次结构图放在论文中,并附上适当的标题说明。
通过以上步骤,你可以构建出一个清晰的层次结构图,为后续的分析工作奠定坚实的基础。
构造判断矩阵是层次分析法(Analytic Hierarchy Process, AHP)中的关键步骤之一。判断矩阵用于量化不同准则或方案之间的相对重要性,进而计算出各个准则或方案的权重。下面是详细的构造判断矩阵的过程:
构造判断矩阵的步骤
- 明确层次结构:
-
- 确定目标层、准则层以及方案层的元素。
- 例如,选择最佳旅游地的目标,考虑的准则包括景色、花费、居住、饮食和交通,备选方案为苏杭、北戴河和桂林。
- 定义判断尺度:
-
- 定义一个标度系统,用于衡量不同准则或方案之间的相对重要性。
- 标度通常为1, 3, 5, 7, 9及其倒数,其中1表示同等重要,3表示稍微重要,5表示明显重要,7表示强烈重要,9表示极端重要。
- 中间值如2, 4, 6, 8可以用来表示介于两个相邻标度之间的相对重要性。
- 构造判断矩阵:
-
- 对于每一层次中的各元素相对于上一层中某一准则的重要性进行两两比较。
- 例如,对于目标层“选择最佳旅游地”,需要构造一个准则层的判断矩阵,即景色、花费、居住、饮食和交通之间的相对重要性。
- 对于准则层中的每一个准则,还需要构造一个方案层的判断矩阵,即苏杭、北戴河和桂林之间的相对重要性。
示例
假设我们有以下层次结构:
- 目标层:选择最佳旅游地 (O)
- 准则层:景色(C1)、花费(C2)、居住(C3)、饮食(C4)、交通(C5)
- 方案层:苏杭(P1)、北戴河(P2)、桂林(P3)
构造准则层的判断矩阵
- 目标层到准则层的判断矩阵:
| O | C1 | C2 | C3 | C4 | C5 |
|----|----|----|----|----|----|
| C1 | 1 | 1/2| 4 | 3 | 3 |
| C2 | 2 | 1 | 7 | 5 | 5 |
| C3 | 1/4| 1/7| 1 | 1/2| 1/3|
| C4 | 1/3| 1/5| 2 | 1 | 1 |
| C5 | 1/3| 1/5| 3 | 1 | 1 |-
- 例如,对于目标层与准则层的判断矩阵,我们需要比较景色、花费、居住、饮食和交通之间的相对重要性。
- 准则层到方案层的判断矩阵:
| C1 | P1 | P2 | P3 |
|----|----|----|----|
| P1 | 1 | 2 | 4 |
| P2 | 1/2| 1 | 2 |
| P3 | 1/4| 1/2| 1 || C2 | P1 | P2 | P3 |
|----|----|----|----|
| P1 | 1 | 1/3| 1/8|
| P2 | 3 | 1 | 1/3|
| P3 | 8 | 3 | 1 || C3 | P1 | P2 | P3 |
|----|----|----|----|
| P1 | 1 | 1 | 3 |
| P2 | 1 | 1 | 3 |
| P3 | 1/3| 1/3| 1 || C4 | P1 | P2 | P3 |
|----|----|----|----|
| P1 | 1 | 3 | 4 |
| P2 | 1/3| 1 | 1 |
| P3 | 1/4| 1 | 1 || C5 | P1 | P2 | P3 |
|----|----|----|----|
| P1 | 1 | 1 | 1/4|
| P2 | 1 | 1 | 1/4|
| P3 | 4 | 4 | 1 |-
- 对于每个准则,我们需要构造一个方案层的判断矩阵,即比较苏杭、北戴河和桂林之间的相对重要性。
注意事项
- 判断矩阵是正互反矩阵,即满足 (a_{ij} \cdot a_{ji} = 1),其中 (a_{ij}) 表示与准则 (j) 相比准则 (i) 的重要性。
- 判断矩阵中的数值需要符合标度系统的定义,即只能是1到9以及它们的倒数。
- 判断矩阵中的元素代表了两两比较的结果,需要确保逻辑上的一致性。
- 如果发现矩阵存在不一致性(即某些比较之间存在矛盾),可以通过调整数值来提高一致性,或者使用一致性比率(CR)来评估和修正不一致性。
- 一旦判断矩阵构造完成,接下来可以进行一致性检验,并计算出各准则或方案的权重。
通过这样的步骤,我们可以系统地构造出层次分析法所需的判断矩阵,为进一步的分析和决策提供依据。
层次分析法(Analytic Hierarchy Process, AHP)是一种结构化的多准则决策分析方法,用于解决涉及多个评价标准和多个备选方案的决策问题。以下是层次分析法的其他步骤的详细介绍:
第三步:计算权重
方法1:算术平均法
- 步骤1:将判断矩阵按列归一化,即每个元素除以该列的总和。
- 步骤2:将归一化后的每列相加(按行求和)。
- 步骤3:将相加后得到的向量中每个元素除以判断矩阵的阶数n,得到权重向量。
例如,对于判断矩阵:
| 景色 | 苏杭 | 北戴河 | 桂林 |
|------|------|--------|------|
| 苏杭 | 1 | 2 | 5 |
| 北戴河| 1/2 | 1 | 2 |
| 桂林 | 1/5 | 1/2 | 1 |- 归一化后的矩阵为:
| 苏杭 | 北戴河 | 桂林 |
|-------|--------|-------|
| 0.5882| 0.5714 | 0.625 |
| 0.2941| 0.2857 | 0.25 |
| 0.1177| 0.1429 | 0.125 |- 未归一化的权重为:
| 苏杭 | 北戴河 | 桂林 |
|-------|--------|-------|
| 1.7846| 0.8298 | 0.3856|- 权重为:
| 苏杭 | 北戴河 | 桂林 |
|-------|--------|-------|
| 0.5949| 0.2766 | 0.1285|方法2:几何平均法
- 步骤1:将判断矩阵的元素按行相乘得到一个新的列向量。
- 步骤2:将新向量的每个元素开n次方根。
- 步骤3:将得到的向量进行归一化处理,即每个元素除以向量的总和。
例如,对于上面的判断矩阵,计算得到的几何平均法权重为:
| 苏杭 | 北戴河 | 桂林 |
|-------|--------|-------|
| 0.5954| 0.2764 | 0.1283|方法3:特征值法
- 步骤1:求出判断矩阵的最大特征值以及其对应的特征向量。
- 步骤2:将特征向量进行归一化处理。
例如,对于判断矩阵:
| 景色 | 苏杭 | 北戴河 | 桂林 |
|------|------|--------|------|
| 苏杭 | 1 | 2 | 5 |
| 北戴河| 1/2 | 1 | 2 |
| 桂林 | 1/5 | 1/2 | 1 |- 最大特征值为3.0055,一致性比例CR=0.0053。
- 归一化后的特征向量(权重)为:
| 苏杭 | 北戴河 | 桂林 |
|-------|--------|-------|
| 0.5954| 0.2764 | 0.1283|第四步:一致性检验
- 步骤1:计算一致性指标CI。
- 步骤2:查找对应的平均随机一致性指标RI。
- 步骤3:计算一致性比例CR,如果CR < 0.1,则认为判断矩阵的一致性可以接受;否则需要对判断矩阵进行修正。
一致性检验是确保判断矩阵的一致性,以保证权重计算的合理性。如果CR大于0.1,则需要修正判断矩阵以提高一致性。例如,可以通过调整矩阵中的数值使其更接近一致矩阵,即使矩阵中的行成倍数关系。
第五步:计算综合得分
- 根据准则层的权重和方案层的权重,计算出每个方案的综合得分,并进行排序。
例如,综合权重矩阵如下:
| 准则 | 苏杭 | 北戴河 | 桂林 |
|-------|------|--------|------|
| 景色 | 0.5954| 0.2764 | 0.1283|
| 花费 | 0.0819| 0.2363 | 0.6817|
| 居住 | 0.4286| 0.4286 | 0.1429|
| 饮食 | 0.6337| 0.1919 | 0.1744|
| 交通 | 0.1667| 0.1667 | 0.6667|- 根据准则权重和方案权重,可以计算出每个方案的总得分。
局限性
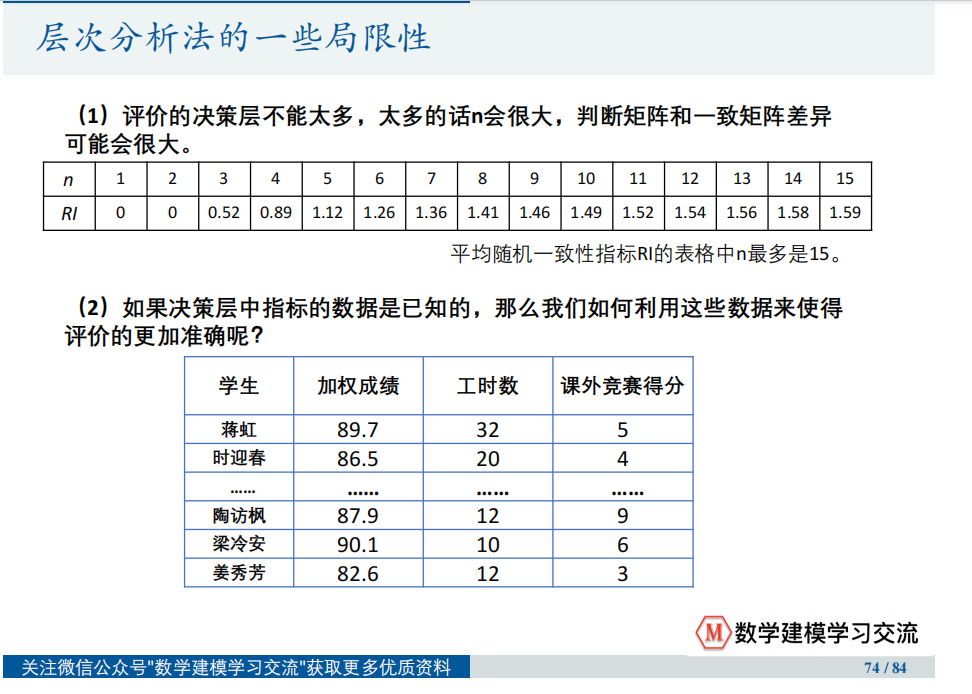
- 评价的决策层不宜过多:决策层过多会导致n很大,判断矩阵与一致矩阵差异可能增大。
- 利用已有数据:如果决策层中的指标数据是已知的,如何利用这些数据以提高评价准确性是一个挑战。
总结
通过以上步骤,层次分析法提供了一种系统的方法来处理多准则决策问题。在实际应用中,需要确保判断矩阵的一致性,并采用多种方法计算权重以提高结果的稳健性。
这篇关于【数学建模】层次分析法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








