聚类：k-Means 和 k-Medoid

2024-08-25 04:12
文章标签 聚类 means medoid

本文主要是介绍聚类：k-Means 和 k-Medoid，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1. 前言

在《对静态分析缺陷报告进行聚类，以降低维护成本》 提到使用 k-Medoid 通过相似缺陷的聚类，来减少程序员对大量缺陷分析的工作量。

k-Medoid 和传统的 k-Means 聚类算法有什么差别呢？

简单的说，K-Medoid 算法是一种基于 K-Means 算法的聚类方法，它通过选择数据集中的点作为中心（medoid），而不是计算均值来代表聚类中心。这种方法对异常值和噪声更加鲁棒，因为它使用的是实际的数据点作为聚类中心，而不是计算出的均值点。

于是将先前的 K-Means 算法做了改进，实现了 K-Medoid 算法。

2. 聚类算法

  • 聚类基本算法步骤
  1. 初始化：选择K个数据点作为初始的质心。可以使用随机选取，也有很多改进的选取方法，以降低迭代的次数；
  2. 分配：将每个数据点分配给最近的质心，形成K个聚类。
  3. 重新计算新的质心：对于每个聚类，找到一个新的质心。
  4. 迭代：重复步骤2和3，直到满足停止条件，如质心不再改变或达到预设的迭代次数。
  5. 终止：当聚类结果稳定或达到迭代次数后，算法终止。

2.1. K-Means 聚类

K-Means 聚类, 在计算每个簇的质心时, 是使用簇的中心点（均值）。

  • K-Means 聚类的质心计算公式
    对于K-Means聚类，每个簇的质心是该簇内所有点的均值。
    假设第( i )个簇包含 N_i个数据点，每个数据点有( d )个特征。
    第( i )个簇的质心 \mu_i​ 的计算公式为：
    \mu_i = \frac{1}{N_i} \sum_{j \in C_i} x_j

其中：

  • \mu_i​ 是第( i )个簇的质心。
  • N_i 是第( i )个簇中的点的数量。
  • C_i是第( i )个簇中的点的集合。
  • x_j 是第( j )个点的坐标。

  • 特点：
    • 简单，易于实现。
    • 对于大规模数据集效率较高。
    • 对初始中心点的选择敏感，可能导致局部最优解。
    • 对异常值和噪声敏感。

  • 适用场景：
    • 数据分布近似为高斯分布。
    • 需要快速聚类结果的场景。

2.2. K-Medoid 聚类

K-Medoid 聚类, 在计算每个簇的质心时, 由一个实际的数据点（Medoid）代表。

  • K-Medoid 聚类的质心计算公式
    K-Medoid聚类不使用质心的概念，而是使用Medoid。Medoid是簇中与其他点距离之和最小的点。
    因此，K-Medoid算法中没有直接计算质心的公式，而是通过以下步骤确定Medoid：
  1. 对于每个簇，计算每个点到该簇内其他所有点的总距离。
  2. 选择总距离最小的点作为Medoid。

这个过程可以表示为：

\text{medoid}_i = \arg \min_{x_j \in C_i} \sum_{x_k \in C_i} d(x_j, x_k)

其中：

  • \text{medoid}_i 是第 i 个簇的 Medoid。

  • d(x_j, x_k)  是点 x_j和x_k 之间的距离。

  • C_i​ 是第( i )个簇中的点的集合。

  • 特点：

    • 对异常值和噪声具有较好的鲁棒性。
    • 计算复杂度较高，因为需要重新计算所有点到 Medoid 的距离。
    • 可以处理非凸形状的聚类。
    • 可能找到全局最优解，因为每次迭代都可能改变 Medoid。

  • 适用场景：

    • 数据分布不规则或包含异常值。
    • 需要更鲁棒的聚类结果。

2.3. K-Means vs K-Medoid

在 K-Medoid 算法中，Medoid 的确定是一个优化问题，需要评估簇内所有点作为 Medoid 时的总距离，并选择使这个总距离最小的点。这个过程通常比 K-Means 中的质心计算更为复杂，因为它涉及到对每个簇内所有点的两两距离计算。

比较项K-MeansK-Medoid
中心点K-Means使用计算出的中心点K-Medoid使用实际的数据点作为中心
鲁棒性K-Means容易受到这些因素的影响K-Medoid对异常值和噪声更鲁棒
计算复杂度K-Means通常更快，因为它只需要计算均值K-Medoid需要计算每个点到Medoid的距离，计算量更大
聚类形状K-Means倾向于创建圆形或球形的簇K-Medoid可以适应更复杂的形状
全局最优对初始中心点的选择敏感，可能导致局部最优解K-Medoid更可能找到全局最优解，因为它在每次迭代中都重新评估所有点作为Medoid的可能性

3. 基础定义

3.1. 距离计算类型

用于测试不同的距离计算公式对聚类结果的影响。

public enum DistanceEnum {EUCLIDEAN("欧氏距离"),MANHATTAN("曼哈顿距离"),MINKOWSKI("闵可夫斯基距离"),CHEBYSHEV("切比雪夫距离"),COSINE("余弦距离"),OTHERS("其他");private String distance;private DistanceEnum(String distance) {this.distance = distance;}
}

3.2. 用例和质心定义

用于存放用例数据或质心。

/*** 用例和质心的定义*/
public class CaseRecord {// 用例 idprivate String id;// 用例的特征键值private Map<String, String> attributeMap;// 用例的向量private double[] vector;// 用例所属的质心private CaseRecord center;// 距离计算类型private DistanceEnum distanceType;// 距离值private double distance;// 聚类用例的数量private int clusterSize;// F-measure rateprivate Rate rate;
}

3.3. 定义算法接口

根据上面的算法流程，定义算法接口

/*** cluster interface* */
public interface Cluster {/*** 聚类过程* * @param k number of cluseter* @param distanceType distance calculate type* @param recordList record list* @return cluster center and cluster records* @throws SdongException module exception*/Map<CaseRecord, List<CaseRecord>> cluster(int k, DistanceEnum distanceType, List<CaseRecord> recordList)throws SdongException;/*** 初始化聚类中心* * @param k number of cluseter* @param recordList record list* @return cluster center*/Map<CaseRecord, List<CaseRecord>> initialCenter(int k, List<CaseRecord> recordList);/*** 将数据分配给最近的质心* * @param k number of cluseter* @param distanceType distance calculate type* @param centerMap cluster center map<center, records list>* @param recordList record list* @throws SdongException module exception*/void putRecordToCenter(int k, DistanceEnum distanceType, Map<CaseRecord, List<CaseRecord>> centerMap,List<CaseRecord> recordList) throws SdongException;/*** 重新计算质心，并判断质心是否变化* * @param k number of cluseter* @param distanceType distance calculate type* @param centerMap current cluster map<center, records list>* @return center changed return true, else returen false* @throws SdongException module exception*/boolean newCenter(int k, DistanceEnum distanceType, Map<CaseRecord, List<CaseRecord>> centerMap)throws SdongException;
}

4. 聚类算法的实现

K-Means 和 K-Medoid 算法都使用相同的聚类过程、初始化聚类中心 和 分配数据到最近的质心 三个方法相同，所以将这些方法放到抽象类：ClusterAbstract 中减少重复代码。

4.1. 聚类过程

对应聚类过程定义，实现聚类过程函数(cluster)。
为了观察和统计需要，增加打印每次质心的变化，同时统计运算过程耗时。

@Override
public Map<CaseRecord, List<CaseRecord>> cluster(int k, DistanceEnum distanceType, List<CaseRecord> recordList)throws SdongException {Stopwatch stopwatch = Stopwatch.createStarted();LOG.info("Cluster process start.");// step 1: 初始化聚类中心Map<CaseRecord, List<CaseRecord>> centers = initialCenter(k, recordList);int loop = 0;boolean change = true;do {loop = loop + 1;AlgorithmUtil.printCenter(loop, centers, false);// step 2: 将数据分配给最近的质心putRecordToCenter(k, distanceType, centers, recordList);AlgorithmUtil.printCenter(loop, centers, false);// step 3: 重新计算质心，并判断质心是否变化change = newCenter(k, distanceType, centers);} while (change);AlgorithmUtil.printCenter(loop, centers, true);stopwatch.stop();LOG.info("Cluster process loop:{}, use: {} ns", loop, stopwatch.elapsed(TimeUnit.NANOSECONDS));return centers;
}

4.2. 初始化聚类中心

为了避免结果的随机性，这里没有使用随机生成初始质心。而先统计了数据中各向量的最小值和最大值。并按 K 均分。得到初始的质心。

后面的 K-Means 和 K-Medoid 都是采用这个方法。

@Override
public Map<CaseRecord, List<CaseRecord>> initialCenter(int k, List<CaseRecord> caseList) {Map<CaseRecord, List<CaseRecord>> centers = new HashMap<>(k);int verctorSize = caseList.get(0).getVector().length;// keep vector value range: min and maxdouble[] min = new double[verctorSize];double[] max = new double[verctorSize];double[] vector;int ind = 0;for (CaseRecord useCase : caseList) {vector = useCase.getVector();for (int i = 0; i < verctorSize; i++) {if (ind == 0) {min[i] = vector[i];max[i] = vector[i];continue;}if (vector[i] < min[i]) {min[i] = vector[i];}if (vector[i] > max[i]) {max[i] = vector[i];}}ind = ind + 1;}for (int j = 0; j < verctorSize; j++) {LOG.info("ind={},min={}, max={}", j, min[j], max[j]);}// initial center per each vector min and max and kdouble distance;CaseRecord center;for (int c = 0; c < k; c++) {center = new CaseRecord();double[] centerVector = new double[verctorSize];center.setVector(centerVector);for (int i = 0; i < verctorSize; i++) {distance = max[i] - min[i];centerVector[i] = min[i] + distance * c / (k - 1);}centers.computeIfAbsent(center, key -> new ArrayList<>());}return centers;
}

4.3. 分配数据到最近的质心

这个也是公共部分，

@Override
public void putRecordToCenter(int k, DistanceEnum distanceType, Map<CaseRecord, List<CaseRecord>> centers,List<CaseRecord> recordList) throws SdongException {CaseRecord nearCenter = null;double minDistance = 0.0;double distance;CaseRecord center;int ind = 0;// clear center related recordsfor (CaseRecord entry : centers.keySet()) {centers.put(entry, new ArrayList<>());}// put record to the nearest centerfor (CaseRecord caseRecord : recordList) {ind = 0;for (Map.Entry<CaseRecord, List<CaseRecord>> entry : centers.entrySet()) {center = entry.getKey();distance = Distance.getDistance(distanceType, caseRecord.getVector(), center.getVector(), 0.0);if (ind == 0) {minDistance = distance;nearCenter = center;ind = ind + 1;continue;}// 余弦相似度 是越大越好if (distanceType == DistanceEnum.COSINE) {if (distance > minDistance) {minDistance = distance;nearCenter = center;}} else {if (distance < minDistance) {minDistance = distance;nearCenter = center;}}}caseRecord.setDistance(minDistance);centers.get(nearCenter).add(caseRecord);}
}

4.4. 重新计算质心

4.4.1. K-Means

public class Kmeans extends ClusterAbstract {private static final Logger LOG = LogManager.getLogger(Kmeans.class);@Overridepublic boolean newCenter(int k, DistanceEnum distanceType, Map<CaseRecord, List<CaseRecord>> centerMap) {boolean change = false;CaseRecord newCenter;int size;int vectorSize;double[] vector;double[] caseVector;// save new centerMap<CaseRecord, List<CaseRecord>> newCenterMap = new HashMap<>(k);Iterator<Map.Entry<CaseRecord, List<CaseRecord>>> iterator = centerMap.entrySet().iterator();Map.Entry<CaseRecord, List<CaseRecord>> entry;while (iterator.hasNext()) {entry = iterator.next();newCenter = new CaseRecord();vectorSize = entry.getKey().getVector().length;// sum vector for centervector = new double[vectorSize];newCenter.setVector(vector);            for (CaseRecord useCase : entry.getValue()) {caseVector = useCase.getVector();for (int i = 0; i < vectorSize; i++) {vector[i] = vector[i] + caseVector[i];}}// avrage vector for centersize = entry.getValue().size();for (int i = 0; i < vectorSize; i++) {vector[i] = vector[i] / size;}// if center change, remove old center and add to new CenterMapif (checkCenterChange(entry.getKey().getVector(), newCenter.getVector())) {iterator.remove();newCenterMap.put(newCenter, new ArrayList<>());change = true;}}// merge new centercenterMap.putAll(newCenterMap);return change;}private static boolean checkCenterChange(double[] vectorOrg, double[] vectorNew) {boolean change = false;int vectorSize = vectorOrg.length;for (int ind = 0; ind < vectorSize; ind++) {if (Double.compare(vectorOrg[ind], vectorNew[ind]) != 0) {return true;}}return change;}
}

4.4.2. K-Medoid

public class Kmedoid extends ClusterAbstract {private static final Logger LOG = LogManager.getLogger(Kmedoid.class);@Overridepublic boolean newCenter(int k, DistanceEnum distanceType, Map<CaseRecord, List<CaseRecord>> centerMap)throws SdongException {boolean change = false;int ind = 0;CaseRecord newCenter = null;Map<CaseRecord, List<CaseRecord>> newCenterMap = new HashMap<>(k);Iterator<Map.Entry<CaseRecord, List<CaseRecord>>> iterator = centerMap.entrySet().iterator();while (iterator.hasNext()) {Map.Entry<CaseRecord, List<CaseRecord>> entry = iterator.next();// calcuate mix distance medoid as new centerdouble minDistance = 0.0;ind = 0;for (CaseRecord medoid : entry.getValue()) {medoid.setDistance(calculateDistenceSum(distanceType, medoid, entry.getValue()));if (ind == 0) {minDistance = medoid.getDistance();newCenter = medoid;ind = ind + 1;continue;}// 余弦相似度 是越大越好if (distanceType == DistanceEnum.COSINE) {if (medoid.getDistance() > minDistance) {minDistance = medoid.getDistance();newCenter = medoid;}} else {if (medoid.getDistance() < minDistance) {minDistance = medoid.getDistance();newCenter = medoid;}}}// if center change, remove old center and add to new CenterMapif (!entry.getKey().equals(newCenter)) {iterator.remove();newCenterMap.put(newCenter, new ArrayList<>());change = true;}}// merege new centercenterMap.putAll(newCenterMap);return change;}private static double calculateDistenceSum(DistanceEnum distanceType, CaseRecord medoid, List<CaseRecord> clusterList)throws SdongException {double sum = 0.0;for (CaseRecord cur : clusterList) {sum = sum + Distance.getDistance(distanceType, medoid.getVector(), cur.getVector(), 0.0);}return sum;}
}

5. 验证测试

5.1. 鸢尾花(Iris)数据集

鸢尾花数据集可以在UCI机器学习库中找到，这是最原始和广泛引用的来源之一。具体地址是：UCI Machine Learning Repository - Iris Dataset

鸢尾花(Iris)数据集它由三种不同品种的鸢尾花的测量数据组成：山鸢尾(setosa)、变色鸢尾(versicolor)和维吉尼亚鸢尾(virginica)。

鸢尾花数据集包含了150个样本，每个样本有四个特征：花萼长度(sepal length)、花萼宽度(sepal width)、花瓣长度(petal length)和花瓣宽度(petal width)。除了样本数据外，每个样本还有一个对应的目标类别，即鸢尾花的品种。

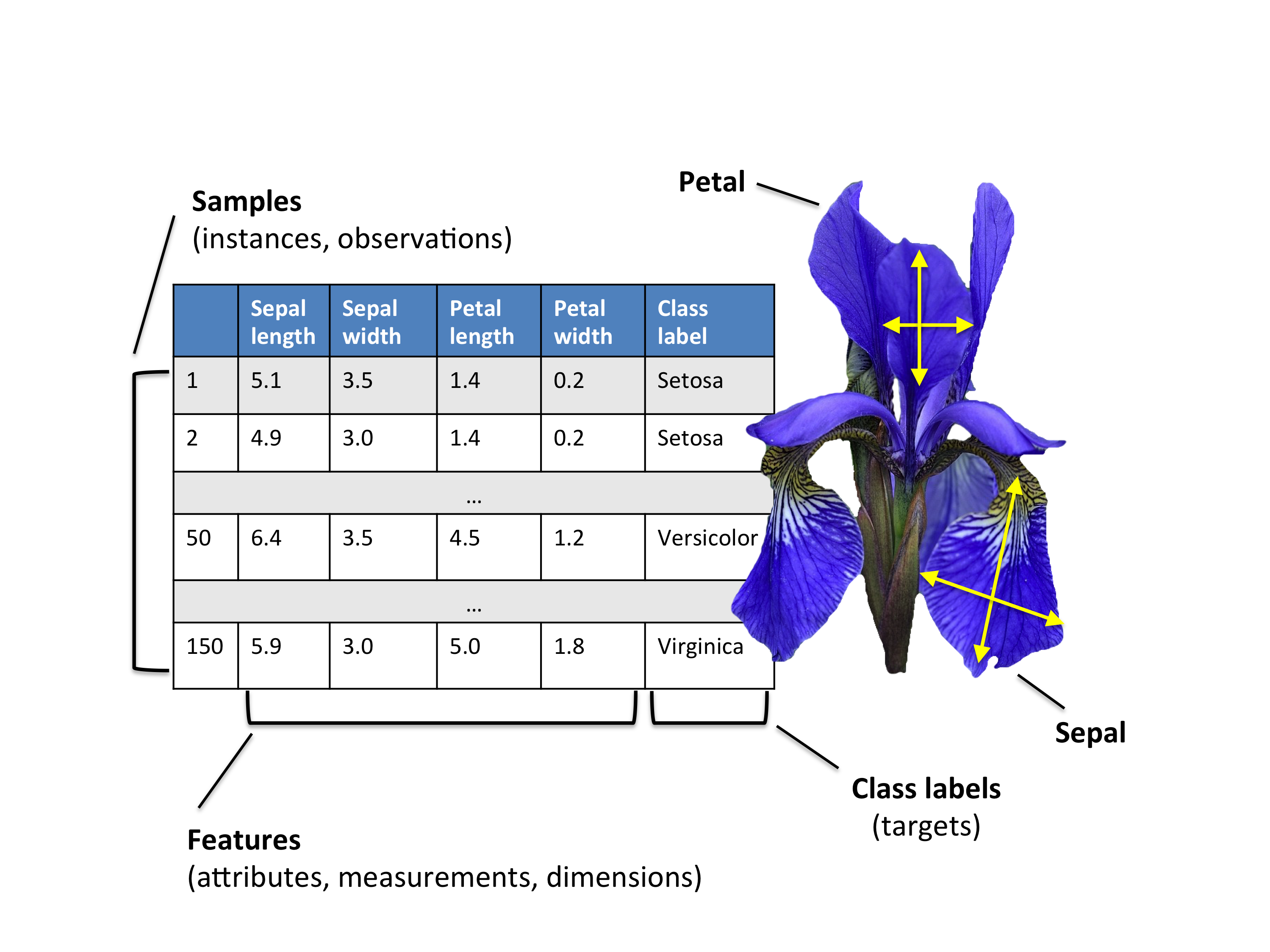
特征名称描述
sepal_length花萼长度
sepal_width花萼宽度
petal length花瓣长度
petal width花瓣宽度
类型山鸢尾(setosa)、变色鸢尾(versicolor)和维吉尼亚鸢尾(virginica)

5.2. 数据集数据

  • 数据分布

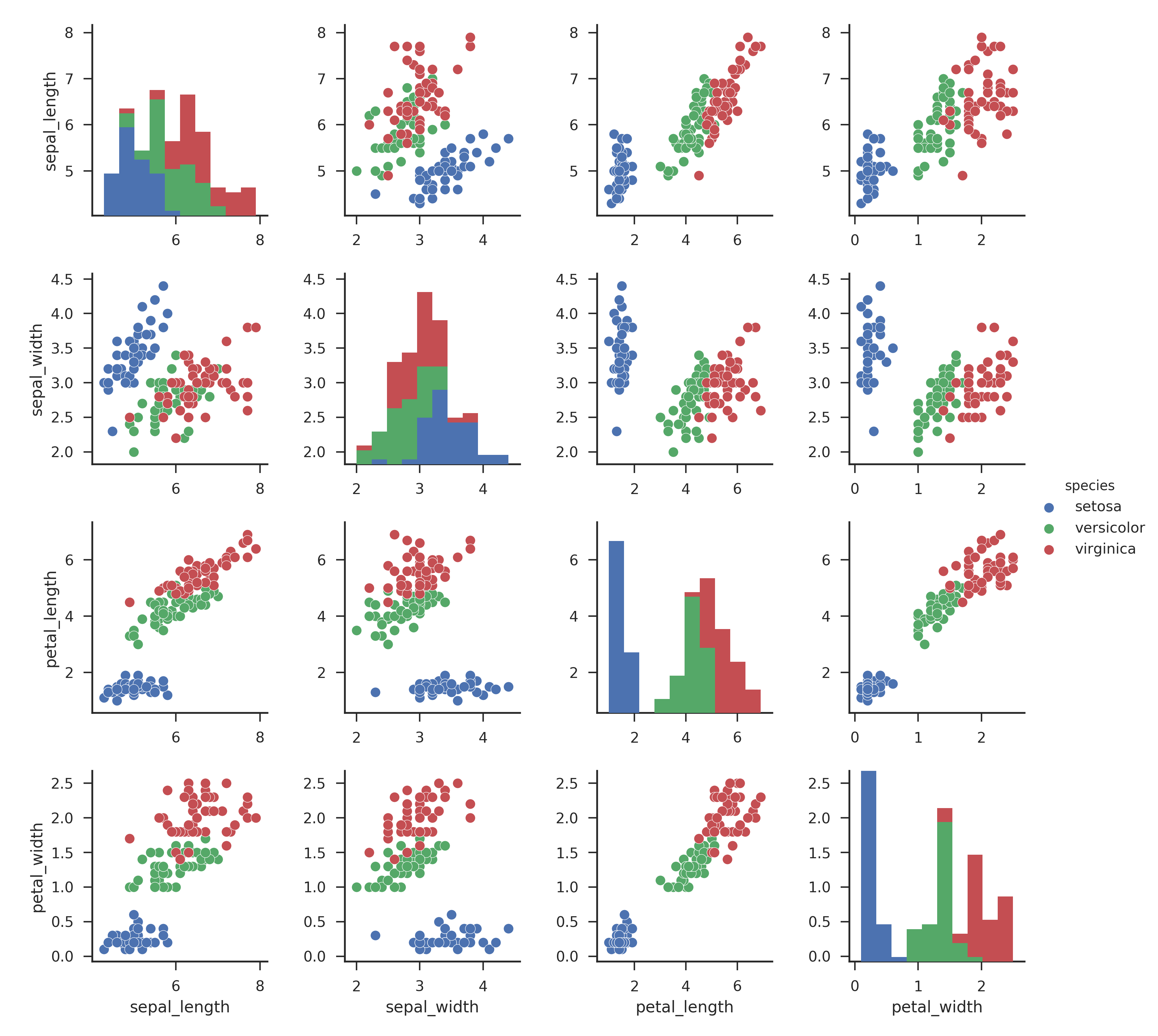
从各维度的投影来看，山鸢尾(setosa) 形状相对独特，通过聚类应该能够容易分辨。但变色鸢尾(versicolor)和维吉尼亚鸢尾(virginica)的形状相似，数据在四个维度上存在一定的重合，并不一定能很好的通过聚类区分出来。

5.3. K-Means 测试结果

  • 测试代码
@Test
void kmeansClusterTest_EUCLIDEAN() {kmeansClusterTest(DistanceEnum.EUCLIDEAN);
}@Test
void kmeansClusterTest_COSINE() {kmeansClusterTest(DistanceEnum.COSINE);
}void kmeansClusterTest(DistanceEnum distanceType) {try {List<CaseRecord> list = ImportData.importIrisData();int k = 3;Kmeans kmeans = new Kmeans();Map<CaseRecord, List<CaseRecord>> centers = kmeans.cluster(k, distanceType, list);Evaluation.evaluationCluster(centers, AIConstants.CLUSTER_CATEGORY);} catch (SdongException e) {LOG.error("{}:{}", e.getErrorPosition(), e.getMessage());fail("should not get exception!");}
}
```

5.3.1. 距离的计算使用：欧氏距离

  • 测试结果
- setosa
id = 01J615ZPC3SDY81Z84QS54KVMP, size = 50, vector: vector[0] = 5.005999999999999,vector[1] = 3.428000000000001,vector[2] = 1.4620000000000002,vector[3] = 0.2459999999999999- virginica
id = 01J615ZPCACZND4PWY1RMCY1BG, size = 38, vector: vector[0] = 6.8500000000000005,vector[1] = 3.073684210526315,vector[2] = 5.742105263157893,vector[3] = 2.0710526315789473- versicolor
id = 01J615ZPCAGEB317YQE24V7WAP, size = 62, vector: vector[0] = 5.901612903225807,vector[1] = 2.748387096774194,vector[2] = 4.393548387096775,vector[3] = 1.4338709677419357Cluster process loop:6, use: 271307900 ns
Evaluation process start.
Cluster:virginica, Precision: 0.9473684210526315, ReCall: 0.72, F1: 0.8181818181818181, purity: 0.0
Cluster:setosa, Precision: 1.0, ReCall: 1.0, F1: 1.0, purity: 0.0
Cluster:versicolor, Precision: 0.7741935483870968, ReCall: 0.96, F1: 0.8571428571428571, purity: 0.0
Avg rate, Precision: 0.907187323146576, ReCall: 0.8933333333333332, F1: 0.8917748917748917, purity: 0.8933333333333333
Evaluateion process use: 6528800 ns

5.3.2. 距离的计算使用：余弦距离

  • 测试结果
- setosa
id = 01J61T8WC7AV9SYXTGGS44XDXH, size = 50, vector: vector[0] = 5.005999999999999,vector[1] = 3.428000000000001,vector[2] = 1.4620000000000002,vector[3] = 0.2459999999999999- virginica
id = 01J61T8WCG7XKZ4M57B4ERCNBG, size = 55, vector: vector[0] = 6.519999999999997,vector[1] = 2.965454545454545,vector[2] = 5.479999999999999,vector[3] = 1.9854545454545451- versicolor
id = 01J61T8WCF05QJ44EJM3GW4GQX, size = 45, vector: vector[0] = 5.946666666666666,vector[1] = 2.757777777777778,vector[2] = 4.204444444444444,vector[3] = 1.2977777777777777Cluster process loop:4, use: 186595900 ns
Evaluation process start.
Cluster:versicolor, Precision: 1.0, ReCall: 0.9, F1: 0.9473684210526316, purity: 0.0
Cluster:setosa, Precision: 1.0, ReCall: 1.0, F1: 1.0, purity: 0.0
Cluster:virginica, Precision: 0.9090909090909091, ReCall: 1.0, F1: 0.9523809523809523, purity: 0.0
Avg rate, Precision: 0.9696969696969697, ReCall: 0.9666666666666667, F1: 0.9665831244778613, purity: 0.9666666666666667
Evaluateion process use: 4176400 ns

5.4. K-Medoid 测试结果

  • 测试代码
@Test
void kMmedoidClusterTest_EUCLIDEAN() {kMmedoidClusterTest(DistanceEnum.EUCLIDEAN);
}@Test
void kMmedoidClusterTest_COSINE() {kMmedoidClusterTest(DistanceEnum.COSINE);
}void kMmedoidClusterTest(DistanceEnum distanceType) {try {List<CaseRecord> list = ImportData.importIrisData();int k = 3;Kmedoid kmedoids = new Kmedoid();Map<CaseRecord, List<CaseRecord>> centers = kmedoids.cluster(k, distanceType, list);Evaluation.evaluationCluster(centers, AIConstants.CLUSTER_CATEGORY);} catch (SdongException e) {LOG.error("{}:{}", e.getErrorPosition(), e.getMessage());fail("should not get exception!");}
}

5.4.1. 距离的计算使用：欧氏距离

  • 测试结果
- versicolor
id = 79, size = 62, vector: vector[0] = 6.0,vector[1] = 2.9,vector[2] = 4.5,vector[3] = 1.5- virginica
id = 113, size = 38, vector: vector[0] = 6.8,vector[1] = 3.0,vector[2] = 5.5,vector[3] = 2.1- setosa
id = 8, size = 50, vector: vector[0] = 5.0,vector[1] = 3.4,vector[2] = 1.5,vector[3] = 0.2Cluster process loop:4, use: 224608300 ns
Evaluation process start.
Cluster:versicolor, Precision: 0.7741935483870968, ReCall: 0.96, F1: 0.8571428571428571, purity: 0.0
Cluster:virginica, Precision: 0.9473684210526315, ReCall: 0.72, F1: 0.8181818181818181, purity: 0.0
Cluster:setosa, Precision: 1.0, ReCall: 1.0, F1: 1.0, purity: 0.0
Avg rate, Precision: 0.9071873231465761, ReCall: 0.8933333333333332, F1: 0.8917748917748917, purity: 0.8933333333333333
2024-08-24 17:37:41.071 INFO [main] Evaluation.java.evaluationCluster.48: Evaluateion process use: 5386900 ns

5.4.2. 距离的计算使用：余弦距离

  • 测试结果
- versicolor
id = 87, size = 45, vector: vector[0] = 6.7,vector[1] = 3.1,vector[2] = 4.7,vector[3] = 1.5- virginica
id = 113, size = 55, vector: vector[0] = 6.8,vector[1] = 3.0,vector[2] = 5.5,vector[3] = 2.1- setosa
id = 39, size = 50, vector: vector[0] = 4.4,vector[1] = 3.0,vector[2] = 1.3,vector[3] = 0.2Cluster process loop:3, use: 188439800 ns
Evaluation process start.
Cluster:setosa, Precision: 1.0, ReCall: 1.0, F1: 1.0, purity: 0.0
Cluster:virginica, Precision: 0.9090909090909091, ReCall: 1.0, F1: 0.9523809523809523, purity: 0.0
Cluster:versicolor, Precision: 1.0, ReCall: 0.9, F1: 0.9473684210526316, purity: 0.0
Avg rate, Precision: 0.9696969696969697, ReCall: 0.9666666666666667, F1: 0.9665831244778613, purity: 0.9666666666666667
Evaluateion process use: 4957100 ns

5.5. 结果分析

  • 结果汇总
聚类方法距离计算迭代次数精度召回率F1纯度
K-Means欧氏距离60.9071870.8933330.8917750.893333
K-Medoid欧氏距离40.9071870.8933330.8917750.893333
K-Means余弦距离40.9696970.9666670.9665830.966667
K-Medoid余弦距离30.9696970.9666670.9665830.966667

  • 分析结论
    • K-Means 和 K-Medoid 在相同距离算法的时候，K-Medoid 迭代次数少于 K-Means。
    • K-Means 和 K-Medoid 在相同距离算法的时候，得到的每个簇内的质心，位置接近；
    • K-Means 和 K-Medoid 聚类结果一致，都在山鸢尾(setosa)的聚类中，完全正确；但在变色鸢尾(versicolor)和维吉尼亚鸢尾(virginica)的聚类中，存在一定的偏差。这与前面数据分布的分析结果一致；
    • K-Means 和 K-Medoid 都在余弦距离的计算比欧式距离的计算得到了更好的聚类效果；
    • 在鸢尾花(Iris)数据集的聚类效果上，K-Means 和 K-Medoid 表现相同。
  • 遗留问题
    • 在分析过程中通过多次计算取均值来衡量资源的消耗，所以这里没有给出资源消耗的对比；
    • 在数据处理上，并为做归一化处理，后面需要考虑归一化对结果的影响；
    • K 值目前是固定的传入的，在实际应用中，需要完善 K 的选取过程；
    • 目前实现的是两类算法的基本算法，未采用一些优化算法，在维度较大的情况，需要改进现有算法。

6. 结论

  • 本文实现了 K-Means 和 K-Medoid 的算法；
  • 使用鸢尾花(Iris)数据集做了两种聚类方法在欧氏距离和余弦距离的聚类测试；
  • 通过精度、召回率、F1、纯度 对聚类效果做了评估；
  • 聚类分析可以揭示数据向量化是否能够捕捉到数据的内在结构和模式；
  • 聚类是验证数据向量化有效手段；
  • 聚类本身并不保证向量化是最优的，因为聚类结果可能受到所选聚类算法、参数设置、数据分布等因素的影响；
  • 聚类分析应与其他数据分析和模型评估方法结合使用，以全面评估数据向量化的有效性。

7. 参考

  • K-Means聚类算法研究综述，华东交通大学学报；
  • K-means clustering algorithms: A comprehensive review, variants analysis, and advances in the era of big data
  • An improved K-medoids algorithm based on step increasing and optimizing medoids
  • Fast and eager k-medoids clustering:O(k)runtime improvement of the PAM,CLARA,and CLARANS algorithms
  • Clustering by fast search and find of density peaks

这篇关于聚类：k-Means 和 k-Medoid的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/1104510。

相关文章

线性代数|机器学习-P36在图中找聚类

线性代数|机器学习-P36在图中找聚类

文章目录 1. 常见图结构2. 谱聚类 感觉后面几节课的内容跨越太大，需要补充太多的知识点，教授讲得内容跨越较大，一般一节课的内容是书本上的一章节内容，所以看视频比较吃力，需要先预习课本内容后才能够很好的理解教授讲解的知识点。 1. 常见图结构 假设我们有如下图结构： Adjacency Matrix:行和列表示的是节点的位置，A[i,j]表示的第 i 个节点和第 j 个
阅读更多...
Spark MLlib模型训练—聚类算法 PIC(Power Iteration Clustering)

Spark MLlib模型训练—聚类算法 PIC(Power Iteration Clustering)

Spark MLlib模型训练—聚类算法 PIC(Power Iteration Clustering) Power Iteration Clustering (PIC) 是一种基于图的聚类算法，用于在大规模数据集上进行高效的社区检测。PIC 算法的核心思想是通过迭代图的幂运算来发现数据中的潜在簇。该算法适用于处理大规模图数据，特别是在社交网络分析、推荐系统和生物信息学等领域具有广泛应用。Spa
阅读更多...
用Pytho解决分类问题_DBSCAN聚类算法模板

用Pytho解决分类问题_DBSCAN聚类算法模板

一：DBSCAN聚类算法的介绍 DBSCAN（Density-Based Spatial Clustering of Applications with Noise）是一种基于密度的聚类算法，DBSCAN算法的核心思想是将具有足够高密度的区域划分为簇，并能够在具有噪声的空间数据库中发现任意形状的簇。 DBSCAN算法的主要特点包括： 1. 基于密度的聚类：DBSCAN算法通过识别被低密
阅读更多...
Spark2.x 入门： KMeans 聚类算法

Spark2.x 入门： KMeans 聚类算法

一 KMeans简介 KMeans 是一个迭代求解的聚类算法，其属于 划分（Partitioning） 型的聚类方法，即首先创建K个划分，然后迭代地将样本从一个划分转移到另一个划分来改善最终聚类的质量。 ML包下的KMeans方法位于org.apache.spark.ml.clustering包下，其过程大致如下： 1.根据给定的k值，选取k个样本点作为初始划分中心；2.计算所有样本点到每
阅读更多...
【ML--13】聚类--层次聚类

【ML--13】聚类--层次聚类

一、基本概念 层次聚类不需要指定聚类的数目，首先它是将数据中的每个实例看作一个类，然后将最相似的两个类合并，该过程迭代计算只到剩下一个类为止，类由两个子类构成，每个子类又由更小的两个子类构成。 层次聚类方法对给定的数据集进行层次的分解，直到某种条件满足或者达到最大迭代次数。具体又可分为： 凝聚的层次聚类（AGNES算法）：一种自底向上的策略，首先将每个对象作为一个簇，然后合并这些原子簇为越来
阅读更多...
第L8周：机器学习｜K-means聚类算法

第L8周：机器学习｜K-means聚类算法

本文为🔗365天深度学习训练营中的学习记录博客 🍖 原作者：K同学啊 | 接辅导、项目定制 🚀 文章来源：K同学的学习圈子深度学习 聚类算法的定义： 聚类就是将一个庞杂数据集中具有相似特征的数据自动归类到一起，称为一个簇，簇内的对象越相似，聚类的效果越好。“相似”这一概念，是利用距离标准来衡量的，我们通过计算对象与对象之间的距离远近来判断它们是否属于同一类别，即是否是同一个簇。 聚类是
阅读更多...
自然语言处理系列五十三》文本聚类算法》文本聚类介绍及相关算法

自然语言处理系列五十三》文本聚类算法》文本聚类介绍及相关算法

注：此文章内容均节选自充电了么创始人，CEO兼CTO陈敬雷老师的新书《自然语言处理原理与实战》（人工智能科学与技术丛书）【陈敬雷编著】【清华大学出版社】 文章目录 自然语言处理系列五十三文本聚类算法》文本聚类介绍及相关算法K-means文本聚类算法原理 总结 自然语言处理系列五十三 文本聚类算法》文本聚类介绍及相关算法 分类和聚类都是文本挖掘中常使用的方法，他们的目的都是将相
阅读更多...
Python计算机视觉编程——第六章 图像聚类

Python计算机视觉编程——第六章 图像聚类

目录 1 K-means聚类1.1 Scipy聚类包1.2 图像聚类1.3 在主成分上可视化图像1.4 像素聚类 2 层次聚类3 谱聚类 聚类可以用于识别，划分图像数据集，组织与导航。 1 K-means聚类 K-means是一种将输入数据划分为k个簇的简单的聚类算法。步骤如下： (1) 以随机或猜测的方式初始化类中心 u i , i = 1 ⋯ k ; u_i,i=1\cd
阅读更多...
Python计算机视觉第六章-图像聚类

Python计算机视觉第六章-图像聚类

目录 6.1 K-means聚类 6.1.1 SciPy聚类包 6.1.2　图像聚类 6.1.3　在主成分上可视化图像 6.1.4　像素聚类 6.2　层次聚类 6.3　谱聚类 6.1 K-means聚类         K-means 是一种将输入数据划分成 k 个簇的简单的聚类算法。K-means 反复提炼初 始评估的类中心，步骤如下： (1) 以随机或猜测
阅读更多...
基于Python的机器学习系列（20）：Mini-Batch K均值聚类

基于Python的机器学习系列（20）：Mini-Batch K均值聚类

简介         K均值聚类（K-Means Clustering）是一种经典的无监督学习算法，但在处理大规模数据集时，计算成本较高。为了解决这一问题，Mini-Batch K均值聚类应运而生。Mini-Batch K均值聚类通过使用数据的子集（mini-batch）来更新簇中心，从而减少了计算量，加快了处理速度。 Mini-Batch K均值算法         Mini-Batch
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2