本文主要是介绍LeeCode Practice Journal | Day50_Graph01,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
( LeeCode) 797. 所有的可能路径
题目:797. 所有可能的路径 - 力扣(LeetCode)
题解:代码随想录 (programmercarl.com)
solution
DFS
public class Solution {public IList<IList<int>> results = new List<IList<int>>();public IList<int> path = new List<int>();public IList<IList<int>> AllPathsSourceTarget(int[][] graph) {int n = graph.Length - 1;pathTra(graph, 0, n);return results;}public void pathTra(int[][] graph, int n, int target){path.Add(n);if(n == target){results.Add(new List<int>(path));path.RemoveAt(path.Count - 1);return;}for(int i = 0; i < graph[n].Length; i ++){pathTra(graph, graph[n][i], target);}path.RemoveAt(path.Count - 1);}
}BFS
public class Solution {public IList<IList<int>> AllPathsSourceTarget(int[][] graph) {IList<IList<int>> results = new List<IList<int>>();Queue<List<int>> queue = new Queue<List<int>>();// 初始化队列,开始时仅有起点queue.Enqueue(new List<int> { 0 });int target = graph.Length - 1;while (queue.Count > 0) {List<int> path = queue.Dequeue();int lastNode = path[path.Count - 1];// 如果路径的最后一个节点是目标节点,将路径加入结果if (lastNode == target) {results.Add(new List<int>(path));} else {// 否则,将相邻节点加入路径,并将新路径加入队列foreach (int neighbor in graph[lastNode]) {List<int> newPath = new List<int>(path) { neighbor };queue.Enqueue(newPath);}}}return results;}
}
summary
(卡码) 98. 所有可达路径(ACM模式)
题目:
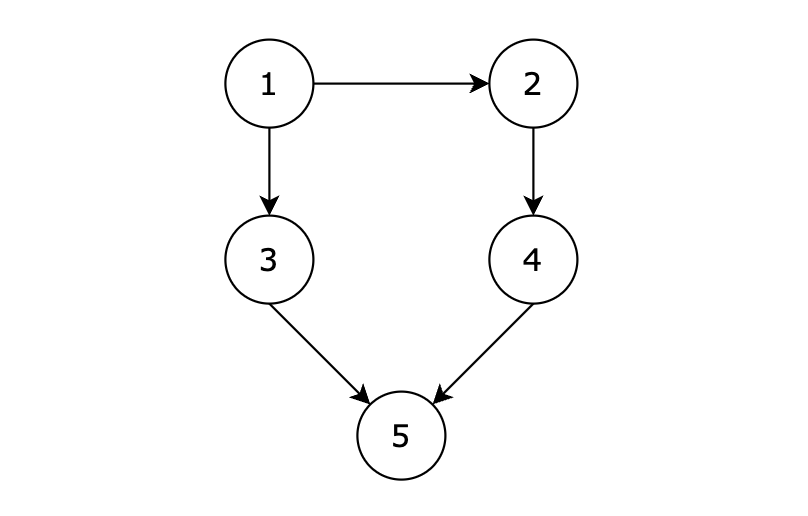
给定一个有 n 个节点的有向无环图,节点编号从 1 到 n。请编写一个函数,找出并返回所有从节点 1 到节点 n 的路径。每条路径应以节点编号的列表形式表示。
输入要求:
第一行包含两个整数 N,M,表示图中拥有 N 个节点,M 条边
后续 M 行,每行包含两个整数 s 和 t,表示图中的 s 节点与 t 节点中有一条路径
输出要求
输出所有的可达路径,路径中所有节点之间空格隔开,每条路径独占一行,存在多条路径,路径输出的顺序可任意。如果不存在任何一条路径,则输出 -1。
注意输出的序列中,最后一个节点后面没有空格! 例如正确的答案是 `1 3 5`,而不是 `1 3 5 `, 5后面没有空格!
solution
邻接表
using System;
using System.Collections.Generic;public class Solution {private List<List<int>> results = new List<List<int>>();private List<int> path = new List<int>();public void AllPathsSourceTarget(int n, List<int>[] graph) {// 从节点 1 开始DFS,注意节点编号从 1 开始path.Add(1);DFS(graph, 1, n);// 如果结果集中没有任何路径,则输出 -1if (results.Count == 0) {Console.WriteLine("-1");} else {foreach (var p in results) {Console.WriteLine(string.Join(" ", p));}}}private void DFS(List<int>[] graph, int node, int target) {if (node == target) {// 到达目标节点,将路径记录下来results.Add(new List<int>(path));return;}foreach (var neighbor in graph[node]) {path.Add(neighbor);DFS(graph, neighbor, target);path.RemoveAt(path.Count - 1);}}
}public class Program {public static void Main(string[] args) {// 读取输入string[] input = Console.ReadLine().Split();int N = int.Parse(input[0]);int M = int.Parse(input[1]);// 构建图List<int>[] graph = new List<int>[N + 1];for (int i = 1; i <= N; i++) {graph[i] = new List<int>();}for (int i = 0; i < M; i++) {string[] edge = Console.ReadLine().Split();int s = int.Parse(edge[0]);int t = int.Parse(edge[1]);graph[s].Add(t);}// 解决问题Solution solution = new Solution();solution.AllPathsSourceTarget(N, graph);}
}
邻接矩阵
using System;
using System.Collections.Generic;public class Solution {private List<List<int>> results = new List<List<int>>();private List<int> path = new List<int>();public void AllPathsSourceTarget(int n, int[,] graph) {// 初始化路径,从节点 1 开始path.Add(1);DFS(graph, 1, n);// 如果没有找到任何路径,输出 -1if (results.Count == 0) {Console.WriteLine("-1");} else {foreach (var p in results) {Console.WriteLine(string.Join(" ", p));}}}private void DFS(int[,] graph, int node, int target) {if (node == target) {results.Add(new List<int>(path));return;}for (int i = 1; i <= target; i++) {if (graph[node, i] == 1) {path.Add(i);DFS(graph, i, target);path.RemoveAt(path.Count - 1);}}}
}public class Program {public static void Main(string[] args) {// 读取输入string[] input = Console.ReadLine().Split();int N = int.Parse(input[0]);int M = int.Parse(input[1]);// 构建邻接矩阵int[,] graph = new int[N + 1, N + 1];for (int i = 0; i < M; i++) {string[] edge = Console.ReadLine().Split();int s = int.Parse(edge[0]);int t = int.Parse(edge[1]);graph[s, t] = 1;}// 解决问题Solution solution = new Solution();solution.AllPathsSourceTarget(N, graph);}
}
这篇关于LeeCode Practice Journal | Day50_Graph01的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!