本文主要是介绍RM双轴云台控制,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
RM机器人上最复杂的控制计构就是双轴云台了,赛场上的情况对双轴云台的控制稳定度与响应灵敏度双方面都提出了很高的要求,云台控制的好坏在一定程度上就能够代表一支队伍的实力。
双轴云台采用的控制算法依然是PID控制算法,关于PID控制算法的原理与实现可以看之前的博客
但双轴云台的控制与底盘控制存在直接的区别在于,底盘是一个单环控制系统,用户对底盘的输入值为底盘的速度期望,底盘的输出也同样是速度。而云台则是一个双环控制系统,用户对云台的输入值为云台的转动角度期望,而云台电机能够直接输出的是转速。
输入是角度的期望,输出的是电机的速度。就是由于这个原因,必须多引入一级控制器,实现将角度控制转换成速度期望,然后再通过第二级控制器完成速度的闭环控制,这就是为什么云台一定要使用双环控制系统。
针对云台的控制系统的结构,我们可以画出简化的系统框图如下:
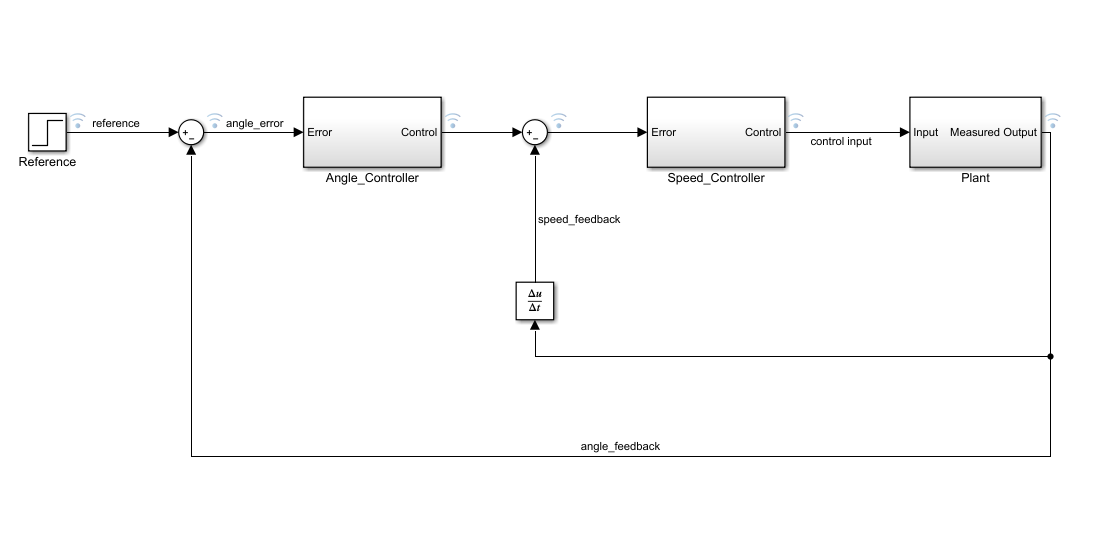
- 外环(角度控制环):负责将角度偏差转换为速度期望。
- 内环(速度控制环):负责根据速度偏差调节电机的输入,以控制电机的转速。
我们给整个系统的输入值reference就是整个云台的角度期望,将其与实际的输出角度angle_feedback(这个值一般是云台电机编码器的反馈角度值或者IMU反馈的角度值)做差,将差值作为角度控制器(Angle_controller)的输入,计算第一环的PID,角度控制器的输出值直接作为速度控制器(Speed_Controller)的输入。输入与角速度的反馈值(一般是IMU反馈的角速度值或者将云台编码器的反馈角度值进行差分得到实际测量的角速度,角度控制器的输出与实际测量的角速度做差,得到速度控制器的输出,该输出值直接给电机。
角度控制器如下:
- 计算角度偏差:
angle_error = reference - angle_feedback。 Speed_desired = Kp * angle_error + Ki * angle_error_integral + Kd * (angle_error_derivative)。
速度控制器如下:
- 计算速度偏差:
speed_error = Speed_desired - Speed_feedback。 - 这里的
Speed_feedback是实际测量的角速度(通过IMU或对编码器反馈的角度值进行差分(即求导)来获取)。具体如下:(1)如果使用IMU,它通常会提供角速度数据作为反馈值,可以直接使用;如果使用编码器,编码器会提供位置信号,需要通过对这个信号进行处理来获取角速度。(2)编码器的输出是角度位置信号,通常是脉冲形式的。要得到角速度,需要对这些脉冲信号进行时间上的差分。差分过程涉及到测量脉冲之间的时间间隔,并计算脉冲之间的频率,即角速度。(3)记录连续两个脉冲到达的时间点,计算时间差 Δt。假设编码器的分辨率是每圈 N 个脉冲,那么一圈的转动对应 N 个脉冲。因此,角速度 ω 可以通过下面的公式计算: (4)由于测量噪声和电子设备的限制,可能需要对测量到的角速度进行数字滤波,以去除高频噪声。(5)编码器的信号可能需要通过模数转换器(ADC)转换为数字信号,然后由微控制器或数字信号处理器(DSP)进行处理。
(4)由于测量噪声和电子设备的限制,可能需要对测量到的角速度进行数字滤波,以去除高频噪声。(5)编码器的信号可能需要通过模数转换器(ADC)转换为数字信号,然后由微控制器或数字信号处理器(DSP)进行处理。
请注意!!!
我经常这里乱掉,一定会要记住angle_feedback是角度,Speed_feedback是角速度,两个是完全不一样的。角度需要姿态角的解算,而角速度直接可以通过陀螺仪读出来。
一般第一次接触双环控制者的疑问是,为什么可以直接将角度控制器的输出作为速度控制器的输入?角度控制器的输出似乎没有什么物理含义,为什么就可以被看成是速度的期望?
从定性的角度来解释这个问题,这是因为角度控制器的输出确实在一定程度上反映了速度的期望,角度控制器的输出值越大,说明总体上角度的误差是比较大的,也就是目前的云台位置和期望的云台位置差的越远,我们就会越希望云台以更快的速度达到期望的位置,速度期望较大;而当云台的实际位置和期望位置接近时,角度控制器的输出较小,同样我们会希望云台尽可能细微的调节自身的位置,因此云台的速度期望就会小。
由此可见位置控制器的输出实际上和速度期望之间是存在正相关关系的,如果将其直接视作简单的线性关系,我们就可以直接将位置控制器的结果作为速度控制器的输入值。
当然,正相关的函数表达形式有很多,并不一定要采用线性的形式,采用线性的原因更多是因为线性的系统会更加的容易分析,如果引入非线性则系统在数学上的复杂度会增加很多。在部分工程中,我也见过使用位置控制器输出的平方或者高次幂作为速度控制器的输入的情况,这样做的好处是系统在偏差较大的位置时响应更加灵敏,而偏差较小时响应变得不灵敏,但是参数调节方面也会变得困难一些,具体使用何种方案要根据实际情况来斟酌。
在simulink中搭建仿真系统,查看系统的输出结果——输入期望为黄线reference,输出为橙线angle_feedback,可以看到系统的输出是趋于期望的,总体来说是一个稳定的系统。
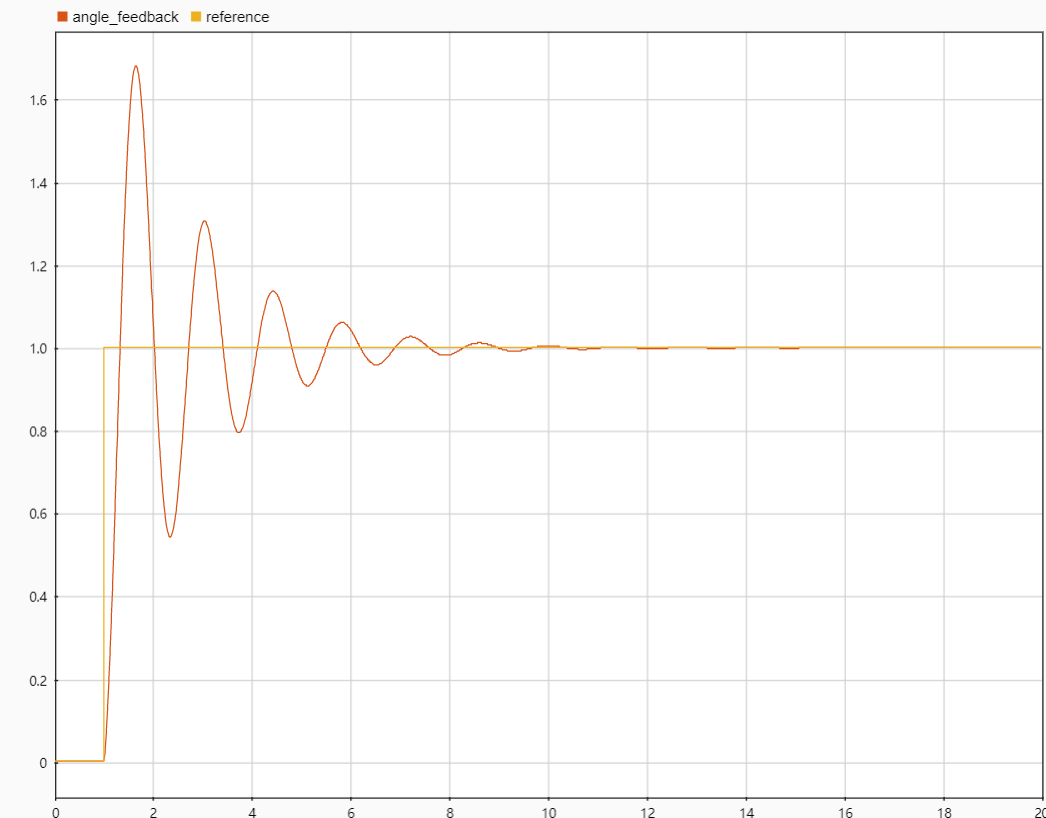
这个系统同样可以信号与系统和自动控制理论的知识进行分析,实际上单环和双环的系统在分析上不会有很大的差别,不过双环控制系统不是简单将两个单环的系统函数直接相乘,速度环与位置环相互之间还是有影响的,在这里就不进行具体的数学推导了,感兴趣的同学可以仿照我在第四章中所进行的数学推导过程,假设一个电机的传递函数,然后自己建立整个系统的闭环传递函数,分析两级PID控制器各自的P,I,D参数的作用。
代码示例
这里依然是采用官方代码来说明双环PID控制的代码实现,新开源的代码结构和之前的不太一样了,可读性也变强了不少,链接如下。
https://github.com/RoboMaster/RoboRTS-Firmware
云台控制的代码和底盘控制非常相似,熟悉了底盘控制代码的话应该会很容易理解。这段代码里还加了一些和模式处理相关的东西,主要还是看我用注释强调的部分的代码
void gimbal_task(void const *argu)
{gimbal_time_ms = HAL_GetTick() - gimbal_time_last;gimbal_time_last = HAL_GetTick();//---------------------------------------------------archive_index++;if (archive_index > 99) //system delay msarchive_index = 0;gimbal_attitude_archive[archive_index][0] = gim.sensor.yaw_gyro_angle;//gim.pid.yaw_angle_fdb;gimbal_attitude_archive[archive_index][1] = gim.pid.pit_angle_fdb;gimbal_attitude_archive[archive_index][2] = gim.pid.yaw_spd_fdb;gimbal_attitude_archive[archive_index][3] = gim.pid.pit_spd_fdb;get_index = archive_index + 50;if( get_index > 99)get_index -= 100;
//----------------------------------------------------mat_init(&yaw_kalman_filter.Q,2,2, yaw_kalman_filter_para.Q_data);mat_init(&yaw_kalman_filter.R,2,2, yaw_kalman_filter_para.R_data);//satori:下面这段代码是根据云台的模式进行初始化,云台的模式不同会影响角度反馈值的输入来源,pid角度的反馈值就是在下面的几个模式处理函数之一中获取的switch (gim.ctrl_mode){case GIMBAL_INIT:init_mode_handler();break;case GIMBAL_NO_ARTI_INPUT:no_action_handler();break;case GIMBAL_FOLLOW_ZGYRO:closed_loop_handler();break;case GIMBAL_PATROL_MODE:shoot.c_shoot_cmd = 0;gimbal_patrol_handler();break;case GIMBAL_POSITION_MODE:pc_position_ctrl_handler();break;case GIMBAL_RELATIVE_MODE:pc_relative_ctrl_handler();break;default:break;}//satori:这里是第一级PID控制器,计算yaw轴和pitch轴的角度控制输出,pid_calc的具体实现可以看第四章,其中对pid_calculate函数的详细分析pid_calc(&pid_yaw, gim.pid.yaw_angle_fdb, gim.pid.yaw_angle_ref);pid_calc(&pid_pit, gim.pid.pit_angle_fdb, gim.pid.pit_angle_ref);//satori:直接将yaw轴和pitch轴第一级控制器的输出结果作为第二级速度控制器的输入gim.pid.yaw_spd_ref = pid_yaw.out;gim.pid.pit_spd_ref = pid_pit.out;//satori:从传感器获取yaw轴和pitch轴的角速度反馈值gim.pid.yaw_spd_fdb = gim.sensor.yaw_palstance;gim.pid.pit_spd_fdb = gim.sensor.pit_palstance;//satori:第二级PID控制器,计算yaw轴和pitch轴的角速度控制输出pid_calc(&pid_yaw_spd, gim.pid.yaw_spd_fdb, gim.pid.yaw_spd_ref);pid_calc(&pid_pit_spd, gim.pid.pit_spd_fdb, gim.pid.pit_spd_ref);//satori:下面这段代码将yaw轴和pitch轴的输出结果装入控制电流的数组/* safe protect */if (gimbal_is_controllable()){glb_cur.gimbal_cur[0] = YAW_MOTO_POSITIVE_DIR*pid_yaw_spd.out;glb_cur.gimbal_cur[1] = PIT_MOTO_POSITIVE_DIR*pid_pit_spd.out;glb_cur.gimbal_cur[2] = pid_trigger_spd.out;}else{memset(glb_cur.gimbal_cur, 0, sizeof(glb_cur.gimbal_cur));gim.ctrl_mode = GIMBAL_RELAX;//pid_trigger.iout = 0;}yaw_angle_ref_js = gim.pid.yaw_angle_ref*1000;yaw_angle_fdb_js = gim.pid.yaw_angle_fdb*1000;yaw_speed_ref_js = pid_yaw.out*1000;yaw_speed_fdb_js = gim.sensor.yaw_palstance*1000;pit_angle_ref_js = gim.pid.pit_angle_ref*1000;pit_angle_fdb_js = gim.pid.pit_angle_fdb*1000;pit_speed_ref_js = pid_pit.out*1000;pit_speed_fdb_js = gim.sensor.pit_palstance*1000;//satori:触发can发送任务,将yaw轴和pitch轴的速度控制输出通过can总线发送给电调osSignalSet(can_msg_send_task_t, GIMBAL_MOTOR_MSG_SEND);osSignalSet(shoot_task_t, SHOT_TASK_EXE_SIGNAL);gimbal_stack_surplus = uxTaskGetStackHighWaterMark(NULL);}
调参技巧
本来不太计划写调参技巧的,在第四章的教程中也说过,PID调参如果不采用系统辨析,或者是对系统建模然后做理论分析的话,更多就是靠经验来做的事情,各人有各人的一套调参习惯,对于各个参数的认知也不太习惯(哪怕是我和我一个队的队友也经常在调参时产生一些分期),所以我这里说的也只是我自己调参时的一些个人经验,拿出来和大家分享分享。
- 调参顺序,可以先角度后速度,也可以先速度后角度,但不管是哪种顺序,都一定要保证速度环的系数不全为0,否则相当于速度环没有在工作,始终没有任何输出提供给电机,电机一点都不会动的。
- 如果是先速度后角度的话,角度环所有系数设置为0时,相当于速度环的期望一直为0,把这个翻译成人话就是调试时,云台的角度应该用手掰到任何一个位置都能自然的停住不动,如果用手缓慢的掰动云台,应该能感受到明显有反抗的力,但是这个力的大小不会随着角度的变化而变化,而且云台的位置也是被推动着改变的。如果手掰动云台的力度变化,则用力越大,反抗的力就也越大。
- 如果是先角度后速度的话,速度环可以只给比例项赋值为1,另外两项设成0。这样做的主要目的是为了在调角度环时尽量闭环速度环内参数带来的影响。这个时候如果用手掰云台的话,除了感受到反抗的力之外,松手后云台角度应该是可以回到原来的位置的,而且手把云台掰的角度越大,反抗的力就也应该越大。
- 尽量不要来回修改两个环的参数,基本的控制变量思想还是得有,控制其他参数不变的情况下针对某一个参数进行调节,调到可能的最好情况之后再更换下一个参数调节。每次调节出的最好参数记得做下记录。
- 整个系统的最终测试一般用给角度环阶跃信号作为期望,或者冲激信号作为期望来进行测试。注意,只能给角度环阶跃输入,如果把阶跃输入给速度环的话,电机就会开始360°旋转了。
我个人的习惯一般还是先位置后速度。云台的参数调节除了和PID参数有关之外,还和控制周期,传感器反馈频率,器件热噪声大小等因素有关,有的时候其实不需要复杂的参数就能有很好的控制效果(我们上个赛季的车子云台双环都只用了比例项系数就调出了不错的控制效果),如果始终调不好的话需要去考虑一下有没有可能是其他因素导致的原因。
结语
这次主要是聊了聊双轴云台控制有关的一些东西,这个做起来其实真的不是很难,很多人容易被云台两个字给吓到,但是实际上上手了就会发现,虽然想要调的很好非常难(不然那些相机云台也不会随随便便就大几百上千的卖了),但是调到能够适应比赛的程度不会非常困难的,重点还是多调,多积累经验。
目前我们在调试PID的时候主要根据时域分析法,即观察时域的响应曲线调节PID参数。(听说还有小伙伴在使用经验调参和玄学调参?)
使用时域分析法可以很方便的体现出系统的动态特性,例如调节时间、超调量等信息,也可以大致衡量系统的稳定性。但是如何才做到准确的判断系统的稳定性,了解系统的带宽,抑制噪声呢?这里给大家介绍一下频域分析法和系统辨识。
下面介绍了对RoboMaster步兵机器人yaw轴云台速度环的系统辨识过程。引入频域分析法、传递函数,系统辨识的基本概念,介绍了J-Scope、Keil和MATLAB的fdatool和system Identification工具的应用技巧。
基本概念
频域分析法
应用频率响应特性研究线性系统的经典方法称为频域分析法。
频率特性的物理意义明确,可以用分析法和实验方法获得。在进行系统分析和设计时可以应用图解法进行,直观方便。
闭环系统的传递函数
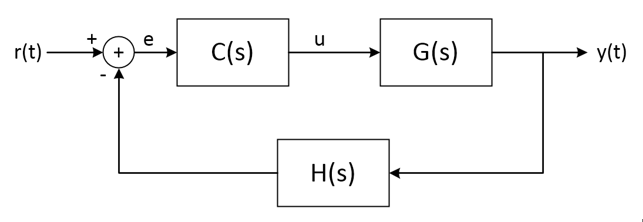
G(s)代表被控对象,C(s)为控制器,H(s)为反馈。
在不考虑扰动的情况下,系统的闭环传递函数为

因此系统可以等效为:
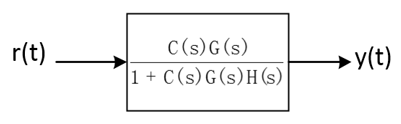
系统的开环传递函数为:
C(s)G(s)H(s),代表回路增益。
注意:此处的开环传递函数是针对闭环系统来说的,不是开环系统的传递函数。
由上面分析可知开环传递函数和闭环传递函数关系紧密,因此系统的开环频率特性很大程度上决定了系统的闭环性能。由于闭环系统包含反馈,校准过程较为复杂,而开环传递函数容易分析和设计,因此工程上常用开环传递函数来分析和设计控制器。
系统辨识
系统的数学模型是对该系统动态本质的一种数学描述,体现实际系统运行中的动态信息。相应的,我们也可以用实验分析方法获得表征过程动态行为的输入输出数据,建立系统的数学模型。
系统辨识得到数学模型可以用于预测系统输出的未来演变,也可以用于设计控制器来对现有系统的做出改进。
基本思路
采集云台的输入输出数据(发送给yaw轴云台的目标角速度和云台的实际角速度),利用系统辨识得到传递函数,然后证明模型的正确性。
实验平台和工具
硬件:RM步兵云台、stm32开发板、J-Link
软件:Keil、J-Scope、MATLAB(fdatool,systemIdentification)
操作步骤
1. 在Yaw轴云台上加载速度环PID控制器,使得系统可以稳定运行
2. 写一个简单的信号发生器,将频率逐渐增加的激励信号输入至PID控制器
3. 采集并记录对应时刻的激励信号和角速度信息
4. 对输入输出数据进行系统辨识得到系统闭环传递函数,用其他方法进行验证
MPU6500滤波设置
查阅MPU6500的技术手册可知,陀螺仪有多个量程和带宽档位可以设置,为了达到更好的测量精度,需要根据应用需求进行设置。
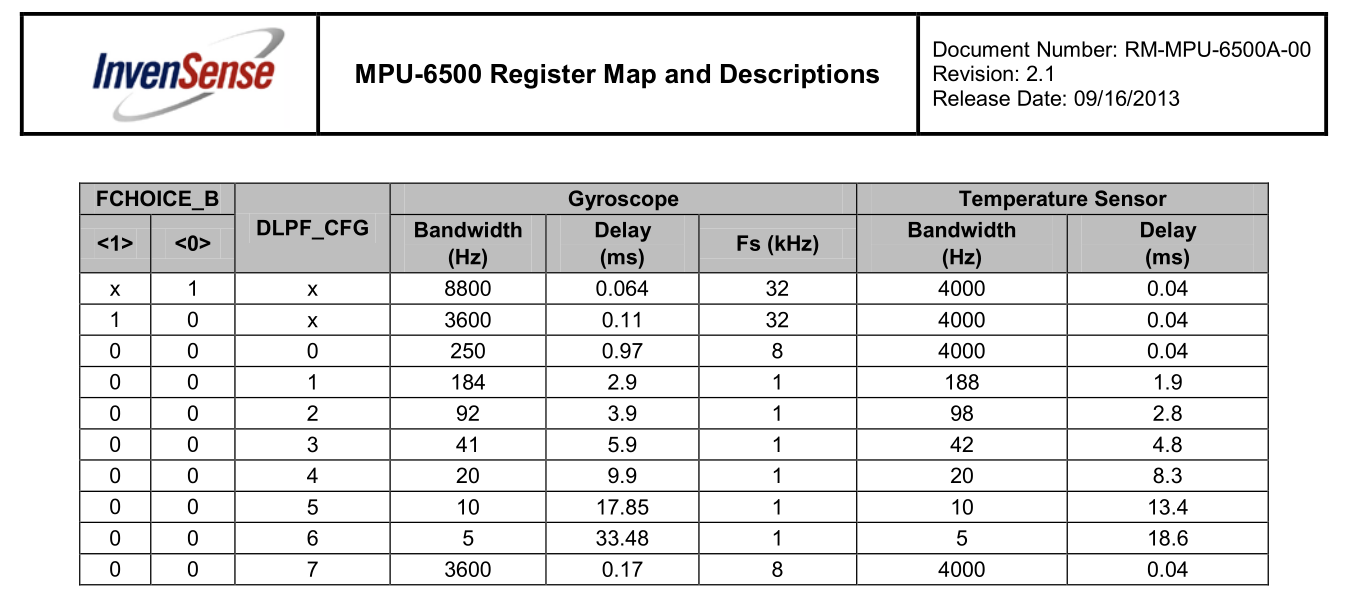

经过初步测试,云台的正常工作角速度在±250°/s以内,因此设置量程为±250dps。
RM 6025电机能响应的电流信号频率为1kHz,根据采样定理,截止频率最高达到500Hz。因此设置MPU6500的带宽为3600Hz, 然后对数据进行低通滤波至500Hz。
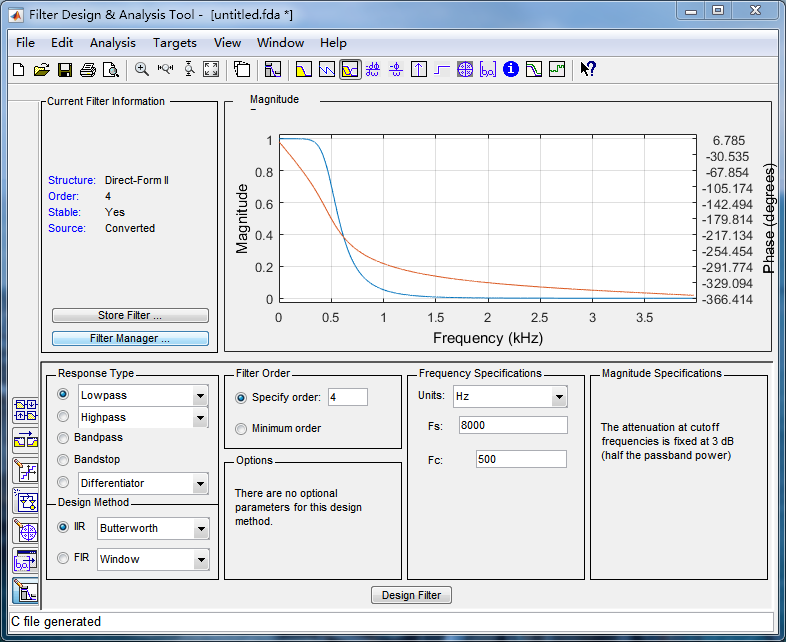
如图所示,用fdatool生成截止频率为500Hz的4阶巴特沃斯滤波器:
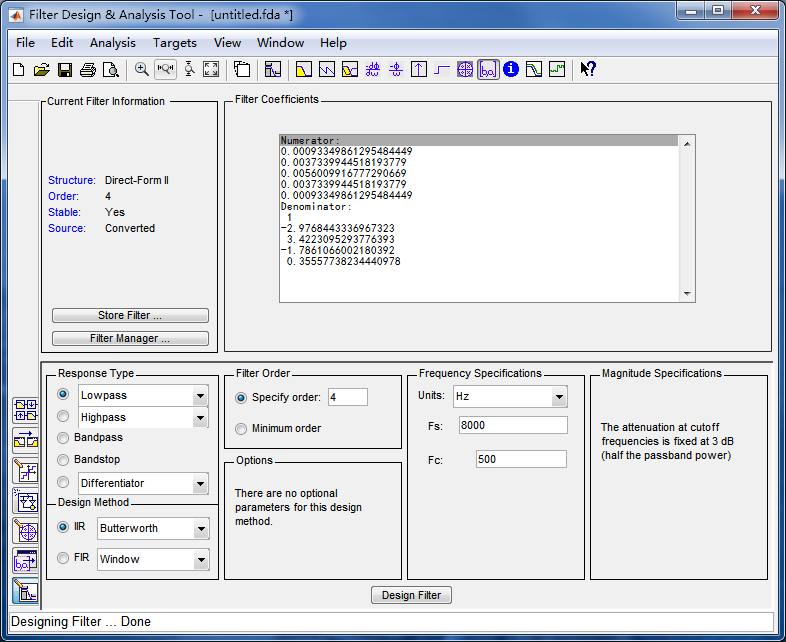
导出系数,将传递函数形式转化为差分形式(具体过程请查阅信号与系统教材),然后在stm32工程里用C语言实现。
速度环PID控制器
根据经验和时域的响应情况,调节PID参数使得云台可以较为稳定的跟随目标角速度。
激励信号的设计
产生频率从1Hz到500Hz变化的正弦信号,每个频率点持续20个周期。由于频率范围较大,且高频部分云台振幅变化较小,为了减少数据量,采用类指数形式的变化趋势。为了保证信号不会发生跳变,在每次信号频率发生变化时都需要从零相位开始,因此周期需要是整数。使用MATLAB生成的激励信号频率如下:
F = ([1:0.5:22, 24:2:40, 50:10:120,200,250,333,500]);
T = round(1000./F); //周期取整
F = 1000./T;
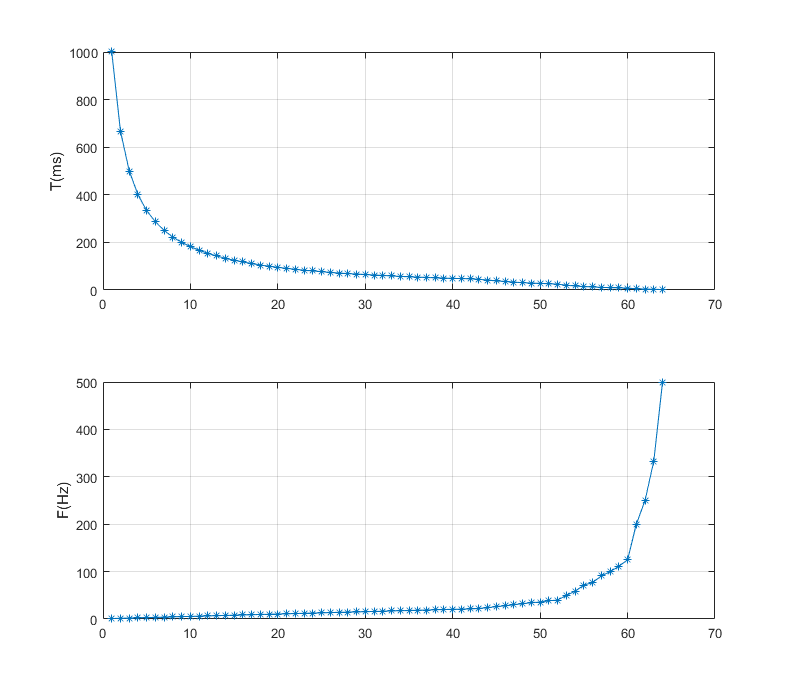
数据采集和处理
编译好stm32嵌入式工程后,配置J-Scope工程,Keil进入调试模式,设置好相关参数后启动程序,用J-Scope记录云台的期望角速度和实际角速度,采集完成后导出数据为csv格式。
注意:J-Scope只能读取整型的数据,因此需要把浮点型的角速度转化为整形(这里采用的方法是乘以1000然后转成整数)
用MATLAB导入csv文件中的数据。
由于采集到的数据前后部分存在激励信号为零的非工作状态,会影响系统辨识的结果,因此需要去除。使用find函数找到激励信号首尾第一个不为零的数据的索引值,然后根据此索引值去掉输入输出信号首尾对应的部分,得到实验所需的时域数据。
处理后的时域数据绘制如下:
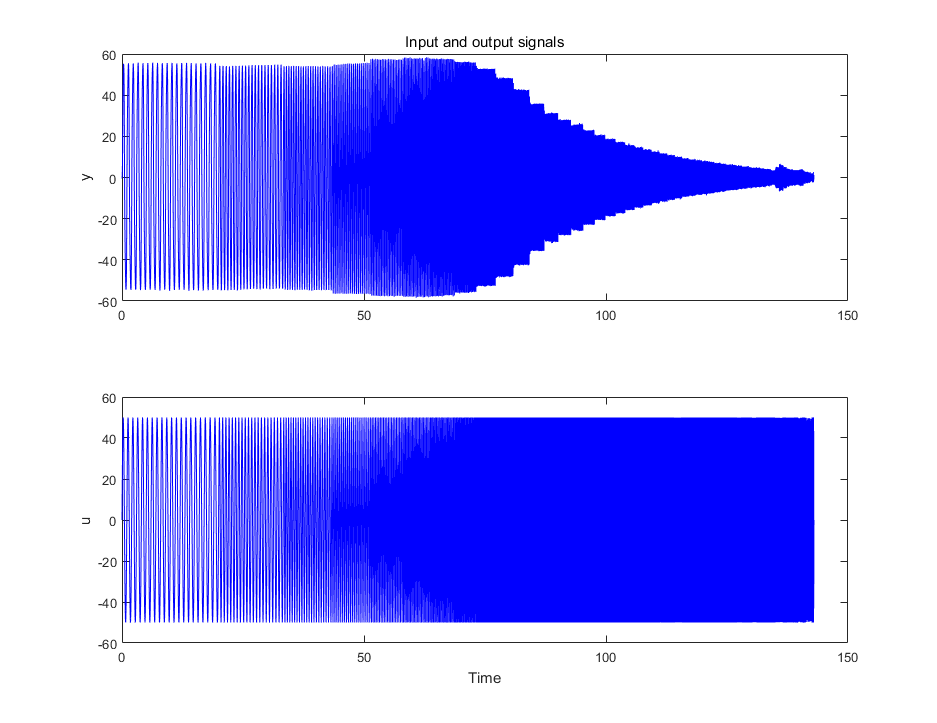
由时域的图像可以明显看到,云台在高频下的振幅由明显衰减。
系统辨识
在MATLAB的命令行窗口输入systemIdentification,打开系统辨识工具箱。
选择 Import data > Time domain data ,打开导入数据对话框,在 input 和 output 选项中键入工作区的输入输出变量名,Starting time 和 Sample time 分别输入 0 和 0.001。其他部分选填。点击 Import 将数据加入System Identification工具,然后关闭对话框。
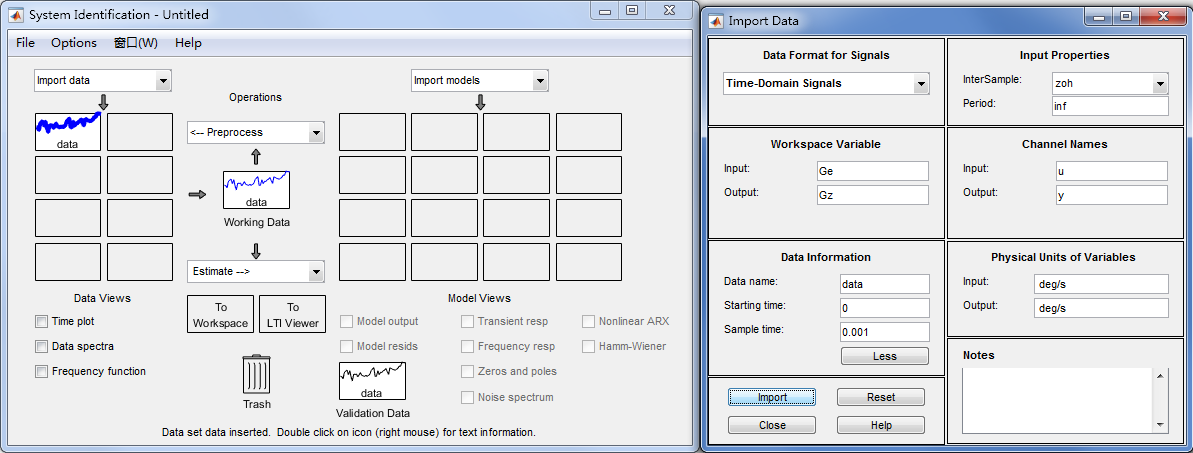
由于本实验数据平均值为零,带宽在500Hz以内,同时需要辨识所有数据,因此无需对数据做去均值、滤波、分割等预处理。直接选择 Estimate > Transfer Function Models 打开传递函数对话框,设置零极点个数分别为1和2,点击 Estimate ,得到系统传递函数如下:

点击 Model output 和 Frequency resp 可以显示传递函数模型的拟合结果和频率响应图。
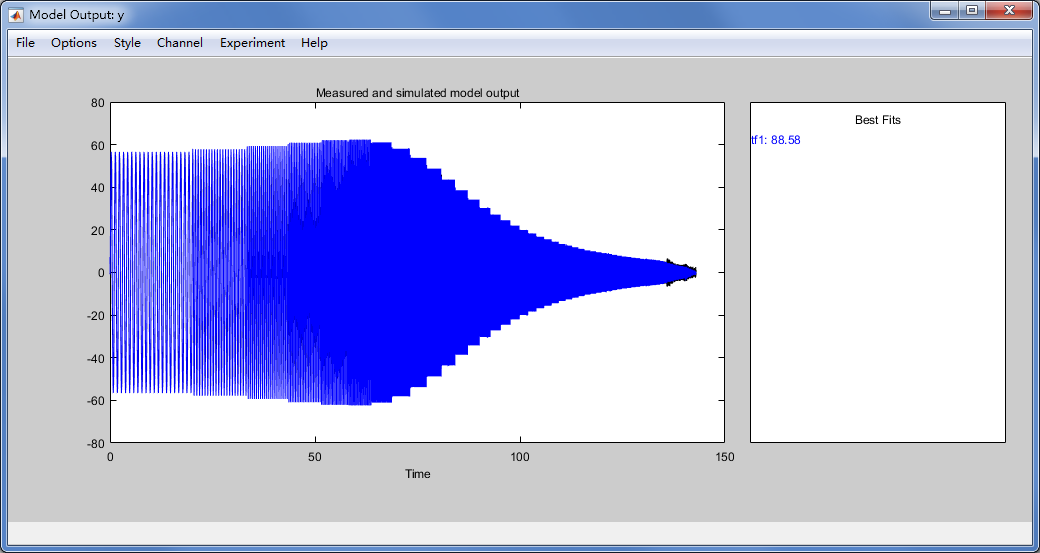
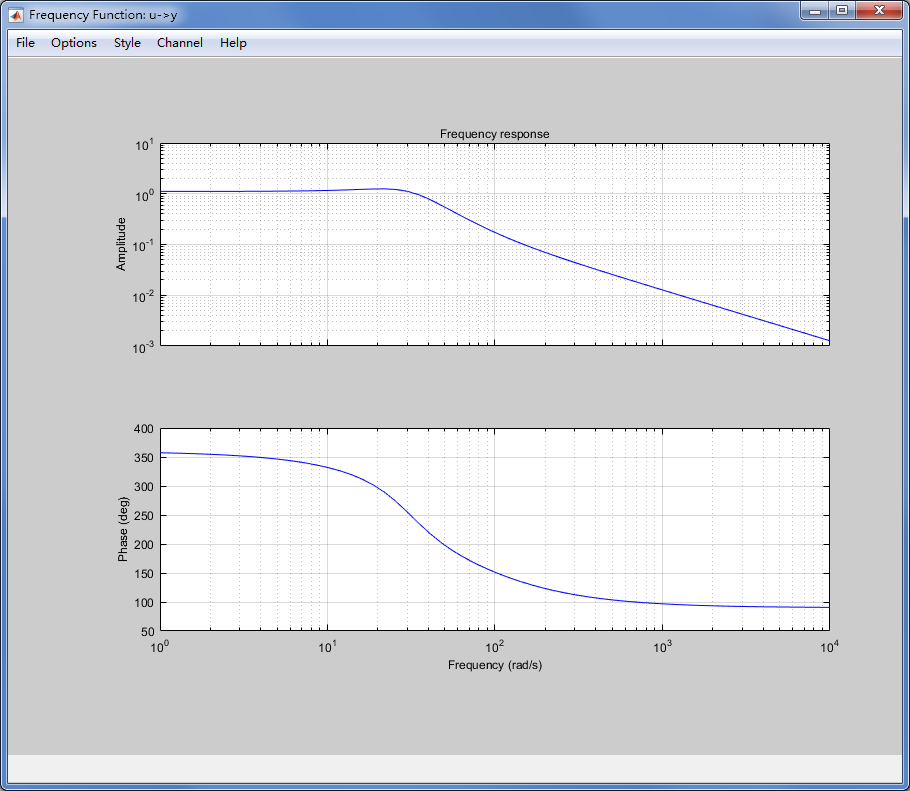
模型验证
为了明确系统辨识得到的传递函数是否可信,可以采用以下两种方法进行验证。
(一)直接测量不同频率下的幅度比和相位差
在stm32的程序中,通过查找一定时间内的云台角速度的极值找出幅度,通过计算输入输出信号上升沿穿过x轴的时间差除以周期来计算该频率下的相位差。
将不同频率点的幅度和相位数据保存在数组中,用Keil的SAVE命令导出内存数据(hex格式),经过处理(删除标志信息、数据分段、16进制转浮点数)后得到实测的频域数据,绘制bode图如下
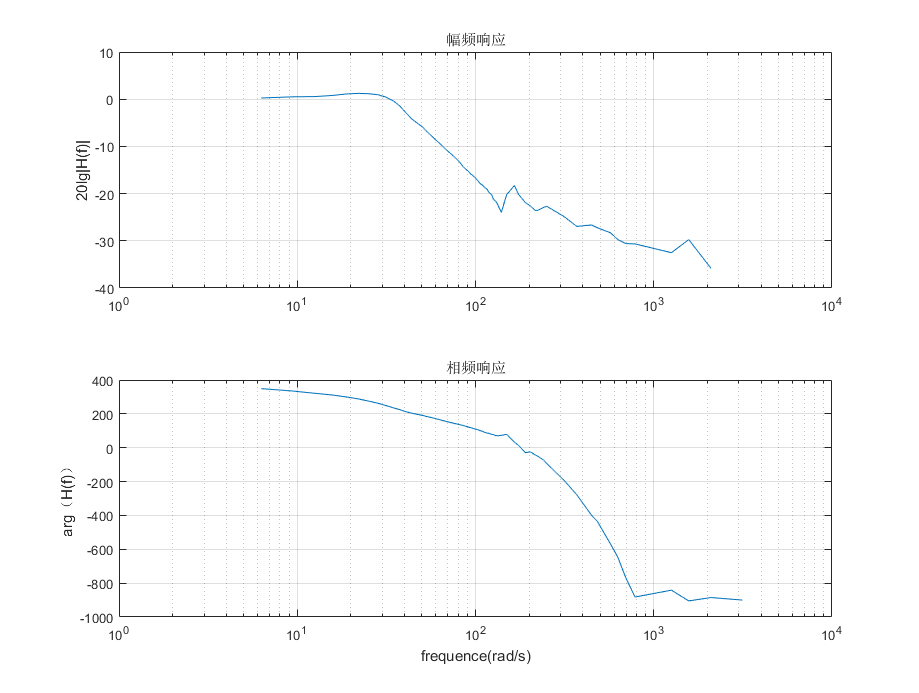
(二)FFT处理时域数据
对时域数据做fft变换,然后计算输入输出数据的幅度比和相位差,得到系统的频率响应:
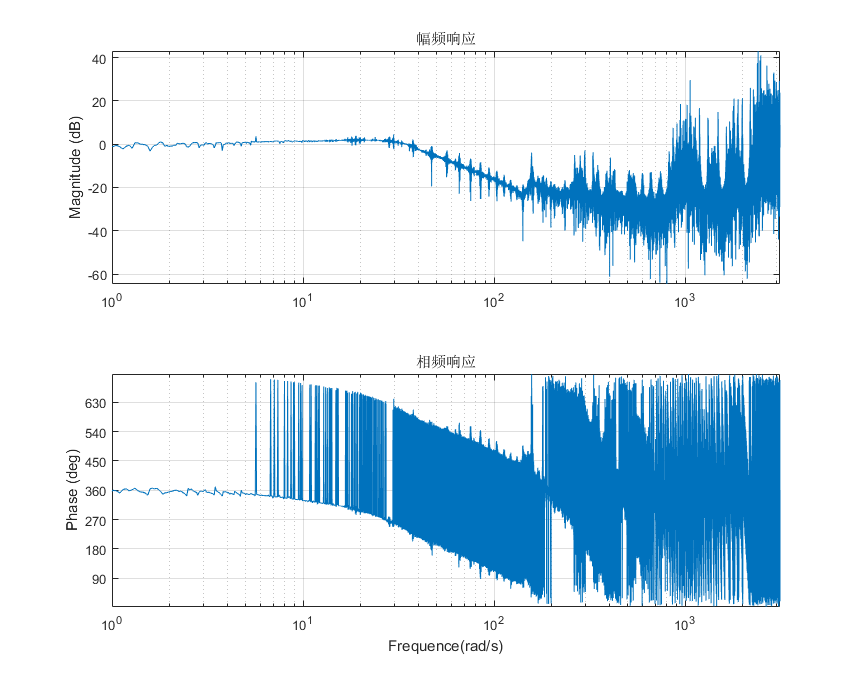
综合对比
对比三种方式得到的频率响应曲线:
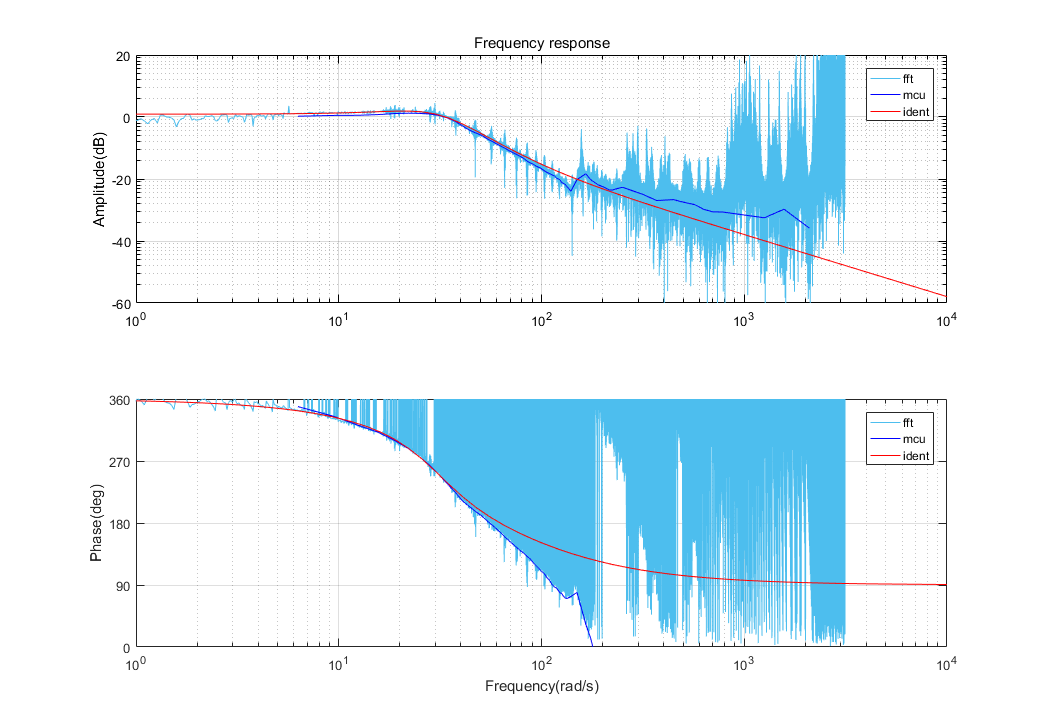
由图可见,在低频部分,系统辨识得到的传递函数能够较好的拟合fft变换的结果和实测的频率响应结果,因此可以用该传递函数来刻画yaw轴云台系统。
由bode图可以看出3dB带宽大概为40rad/s,实际意义就是该云台系统能够响应的频率6.4Hz以内。
得到系统闭环传递函数后,经过处理可以得到开环传递函数进一步分析系统稳定性,还可以用频率分析法对环路进行整形,从而达到我们想要的性能。
这篇关于RM双轴云台控制的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







