销售预测数据挖掘实战V2.0

本文主要是介绍销售预测数据挖掘实战V2.0，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1、概述

沃尔玛全年都会举办几次促销减价活动。这些减价活动都是在重要节假日之前进行的，其中最大的四个节假日是超级碗、劳动节、感恩节和圣诞节。包括这些节假日在内的几周在评估中的权重是非节假日周的五倍。在缺乏完整/理想历史数据的情况下，对这些节假日周的降价影响进行建模，是此次竞争所面临的部分挑战。我们提供了位于不同地区的 45 家沃尔玛商店的历史销售数据。

数据集信息这是 2010-02-05 至 2012-11-01 期间的历史销售数据，字段情况：

Store: 商店 - 商店编号
Date: 日期 - 销售的星期
Weekly_Sales - 指定商店的销售额
Holiday_Flag - 本周是否为特殊假日周 1 - 假日周 0 - 非假日周
Temperature: 温度 - 销售当天的温度
Fuel_Price: 燃料价格 - 该地区的燃料成本
CPI - 现行消费价格指数
Unemployment: 失业率 - 当时的失业率
Holiday Events: 假日活动
Super Bowl: 超级碗 12-Feb-10, 11-Feb-11, 10-Feb-12, 8-Feb-13
Labour Day: 劳动节 10-Sep-10, 9-Sep-11, 7-Sep-12, 6-Sep-13
Thanksgiving: 感恩节 26-Nov-10, 25-Nov-11, 23-Nov-12, 29-Nov-13
Christmas: 圣诞节 31-Dec-10, 30-Dec-11, 28-Dec-12, 27-Dec-13

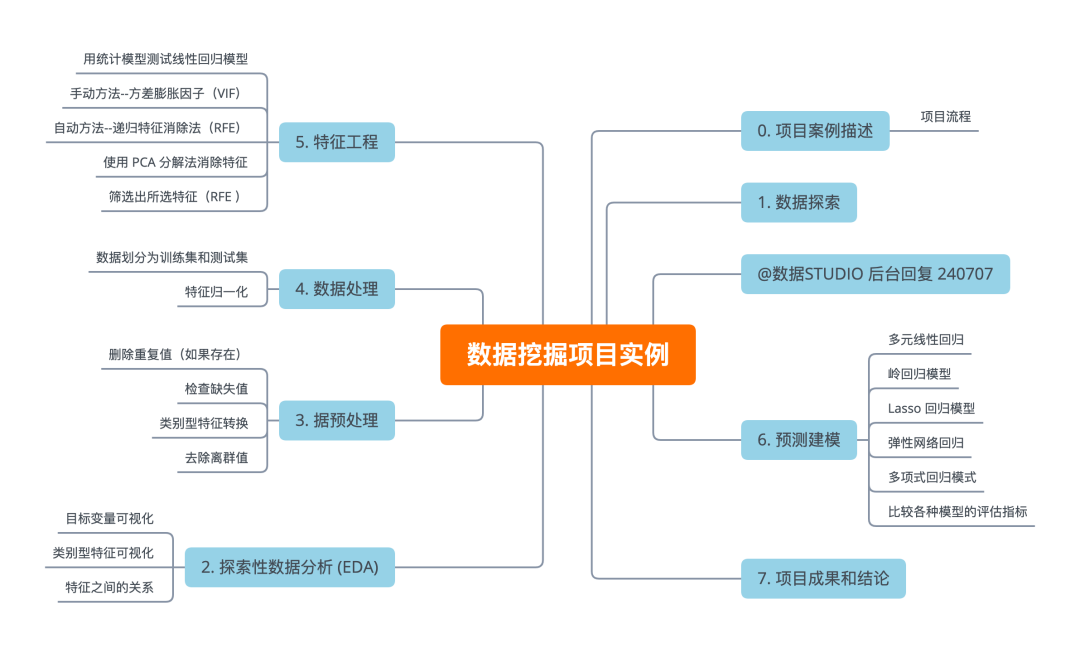
2、项目流程

了解数据集并进行清理（如果需要）。
建立回归模型，利用单一和多重特征预测销售额。
同时评估模型并比较各自的得分，如 R2、RMSE 等。

我们的目标是通过制定行动计划来解决问题陈述，以下是一些必要的步骤：

数据探索
探索性数据分析（EDA）
数据预处理
数据处理
特征选择/提取
预测建模
项目成果与结论

3、数据探索

本项目所用python库如下：

import os
import math
import numpy as np
import pandas as pd
import seaborn as sns
from IPython.display import displayfrom statsmodels.formula import api
from sklearn.feature_selection import RFE
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from statsmodels.stats.outliers_influence import variance_inflation_factorfrom sklearn.decomposition import PCA
from sklearn.linear_model import Ridge
from sklearn.linear_model import Lasso
from sklearn.linear_model import ElasticNet
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import RandomForestClassifier
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_errorimport matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = [10,6]import warnings 
warnings.filterwarnings('ignore')

3.1、导入数据集

df = pd.read_csv('Walmart.csv') # 完整数据集和代码
display(df.head())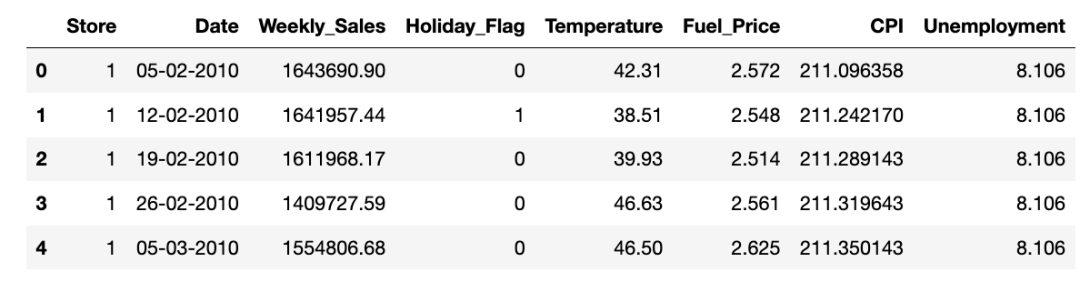

该数据包含 8 个特征 & 6435 个样本.

3.2、重构 columns

df.Date=pd.to_datetime(df.Date)df['weekday'] = df.Date.dt.weekday
df['month'] = df.Date.dt.month
df['year'] = df.Date.dt.yeardf.drop(['Date'], axis=1, inplace=True)#,'month'
target = 'Weekly_Sales'
features = [i for i in df.columns if i not in [target]]
original_df = df.copy(deep=True)df.head()

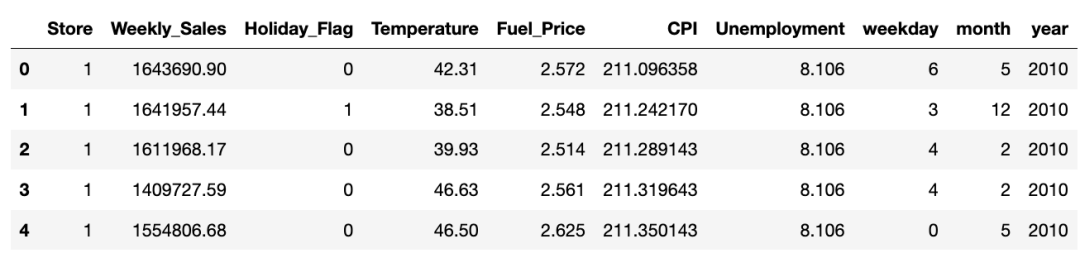
检查所有列信息

df.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 6435 entries, 0 to 6434
Data columns (total 10 columns):#   Column        Non-Null Count  Dtype  
---  ------        --------------  -----  0   Store         6435 non-null   int64  1   Weekly_Sales  6435 non-null   float642   Holiday_Flag  6435 non-null   int64  3   Temperature   6435 non-null   float644   Fuel_Price    6435 non-null   float645   CPI           6435 non-null   float646   Unemployment  6435 non-null   float647   weekday       6435 non-null   int64  8   month         6435 non-null   int64  9   year          6435 non-null   int64  
dtypes: float64(5), int64(5)
memory usage: 502.9 KB

检查每个特征的唯一值个数

df.nunique().sort_values()

Holiday_Flag       2
year               3
weekday            7
month             12
Store             45
Unemployment     349
Fuel_Price       892
CPI             2145
Temperature     3528
Weekly_Sales    6435
dtype: int64

检查每个特征中唯一的行数

nu = df[features].nunique().sort_values()
nf = []; cf = []; nnf = 0; ncf = 0; for i in range(df[features].shape[1]):if nu.values[i]<=45:cf.append(nu.index[i])else: nf.append(nu.index[i])

该数据集包含 4 个数值型 & 5 个类别型特征。

检查所有列的统计量信息

display(df.describe())

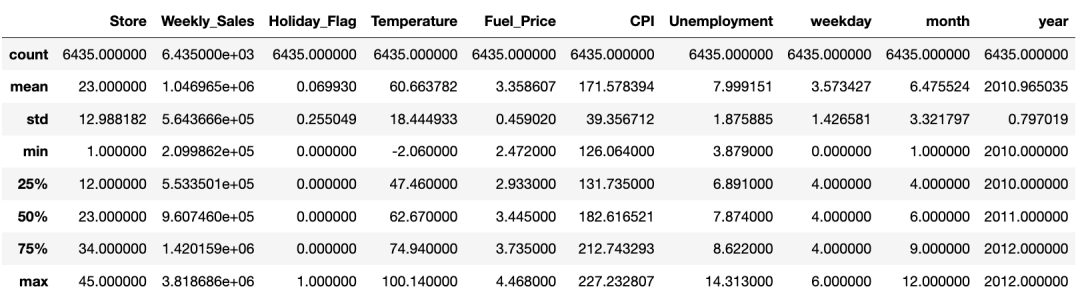
统计数据似乎没有问题，我们对数据集做进一步分析。

4、探索性数据分析 (EDA)

4.1、目标变量可视化

我们首先分析一下目标变量的分布情况。（由于篇幅限制，可视化部分直接贴图，其余展示主要代码）

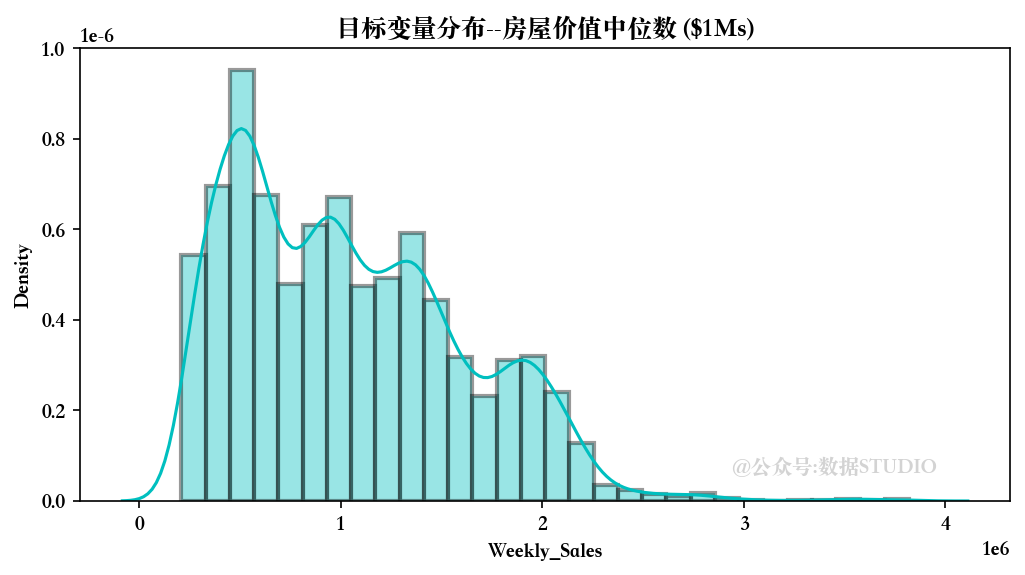
目标变量似乎呈正态分布，平均约为 20 个单位。

4.2、类别型特征可视化

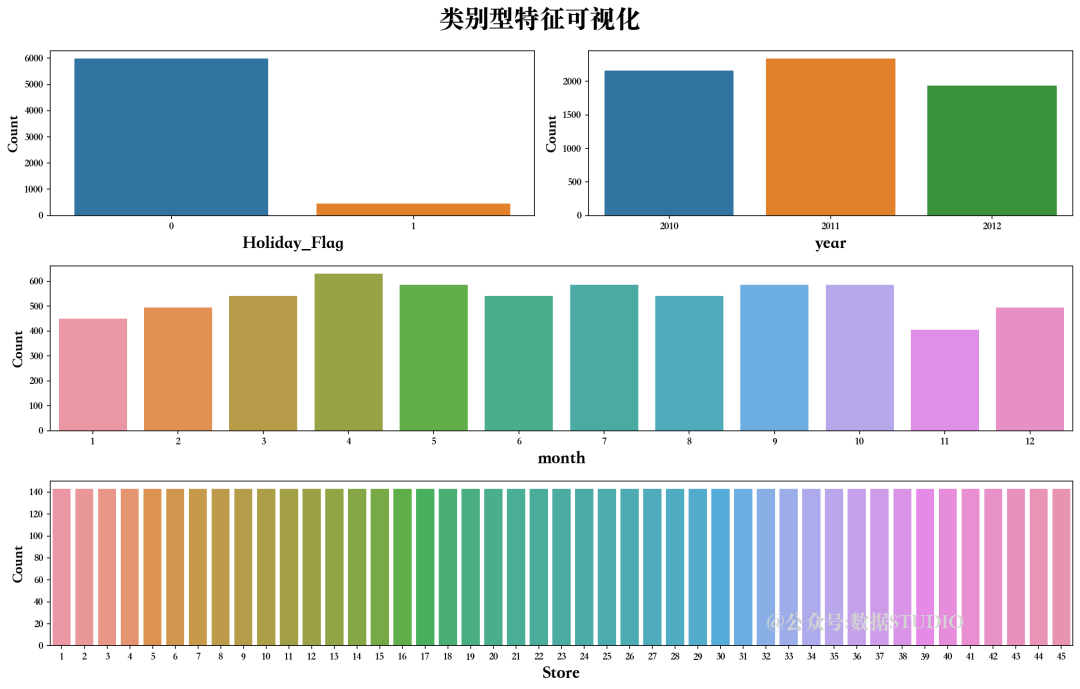
4.3、数值型特征可视化

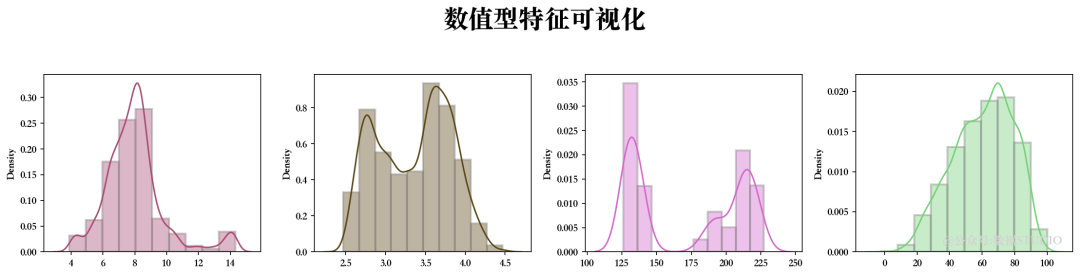
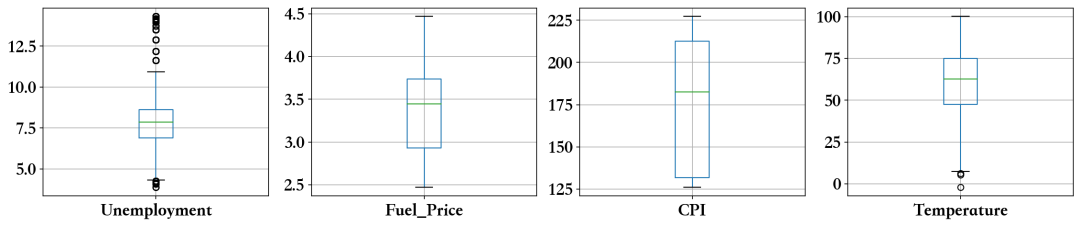
似乎有一些异常值，接下来我们需要解决这些问题...

4.4、特征之间的关系

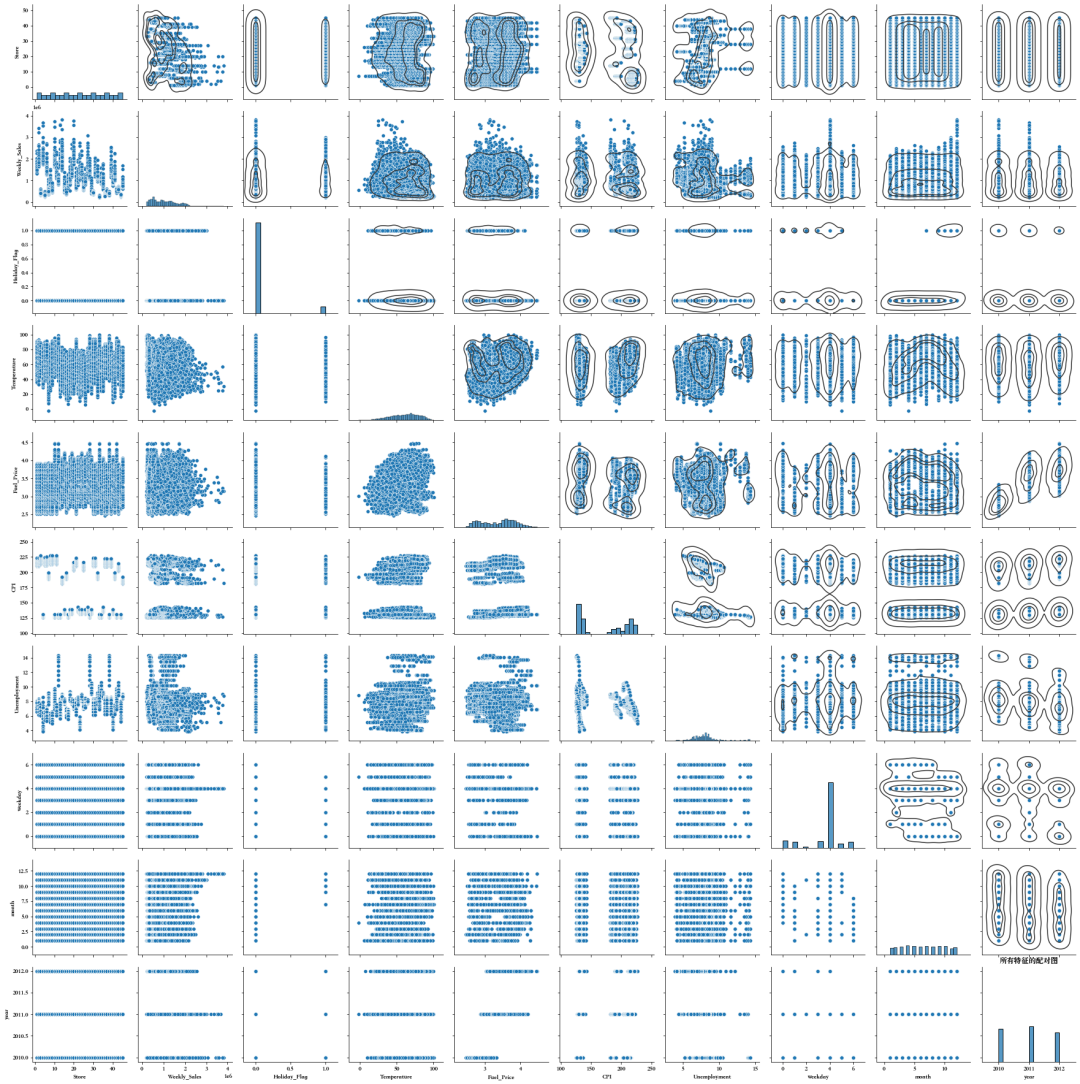
我们可以发现一些特征具有线性关系，接下来需要进一步分析检测多重共线性。

5、据预处理

5.1、删除重复值（如果存在）

df.drop_duplicates(inplace=True)

删除重复值数量---> 482

5.2、检查缺失值

nvc = pd.DataFrame(df.isnull().sum().sort_values(), columns=['Total Null Values'])
nvc['Percentage'] = round(nvc['Total Null Values']/df.shape[0],3)*100
print(nvc)

              Total Null Values  Percentage
Store                         0         0.0
Weekly_Sales                  0         0.0
Holiday_Flag                  0         0.0
Temperature                   0         0.0
Fuel_Price                    0         0.0
CPI                           0         0.0
Unemployment                  0         0.0
weekday                       0         0.0
month                         0         0.0
year                          0         0.0

数据集没有任何不一致的值。

5.3、类别型特征转换

for i in fcc:if df[i].nunique()==2:d[i]=pd.get_dummies(df[i], drop_first=True, prefix=str(i))if (df[i].nunique()>2):df = pd.concat([df.drop([i], axis=1), pd.DataFrame(pd.get_dummies(df3[i], drop_first=True, prefix=str(i)))],axis=1)

经 One-Hot 编码的特征: 
Holiday_Flag经哑变量编码的特征:
year
weekday
month
Store

5.4、去除离群值

features1 = nf
for i in features1:Q1 = df1[i].quantile(0.25)Q3 = df1[i].quantile(0.75)IQR = Q3 - Q1df1 = df1[df1[i] <= (Q3+(1.5*IQR))]df1 = df1[df1[i] >= (Q1-(1.5*IQR))]df1 = df1.reset_index(drop=True)
display(df1.head())

删除离群值前, 数据集有 6435 个样本。
删除离群值后，数据集有 5953 个样本。

预处理后的最终数据集大小：数据清洗后, 482个样本被抛弃, 占总数据量的 7.49%

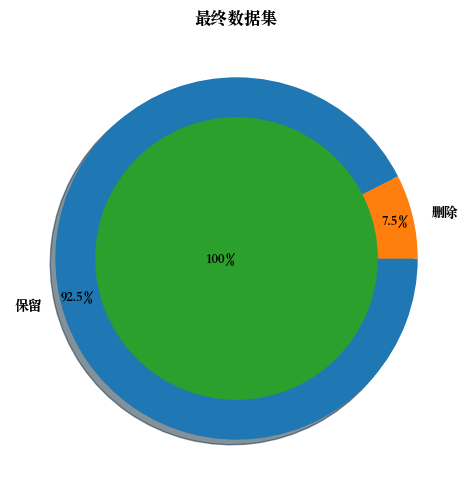
6、数据处理

6.1、数据划分为训练集和测试集

X = df.drop([target],axis=1)
Y = df[target]
Train_X, Test_X, Train_Y, Test_Y = train_test_split(X, Y, train_size=0.8, test_size=0.2, random_state=100)

原始数据集 --->  (5953, 68) (5953,) 
训练数据集  --->  (4762, 68) (4762,) 
测试数据集   --->  (1191, 68)  (1191,)

6.2、特征归一化

std = StandardScaler()
Train_X_std = std.fit_transform(Train_X)
Test_X_std = std.transform(Test_X)

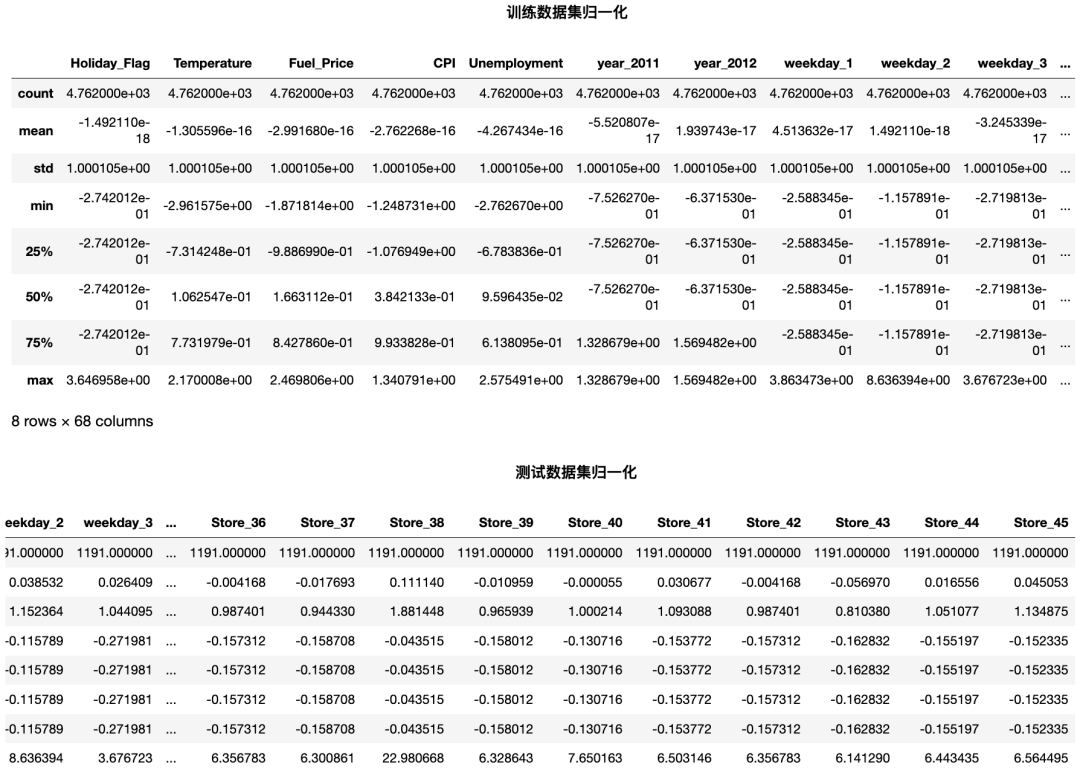
7、特征工程

首先通过相关性矩阵查看各个特征间的相关性。

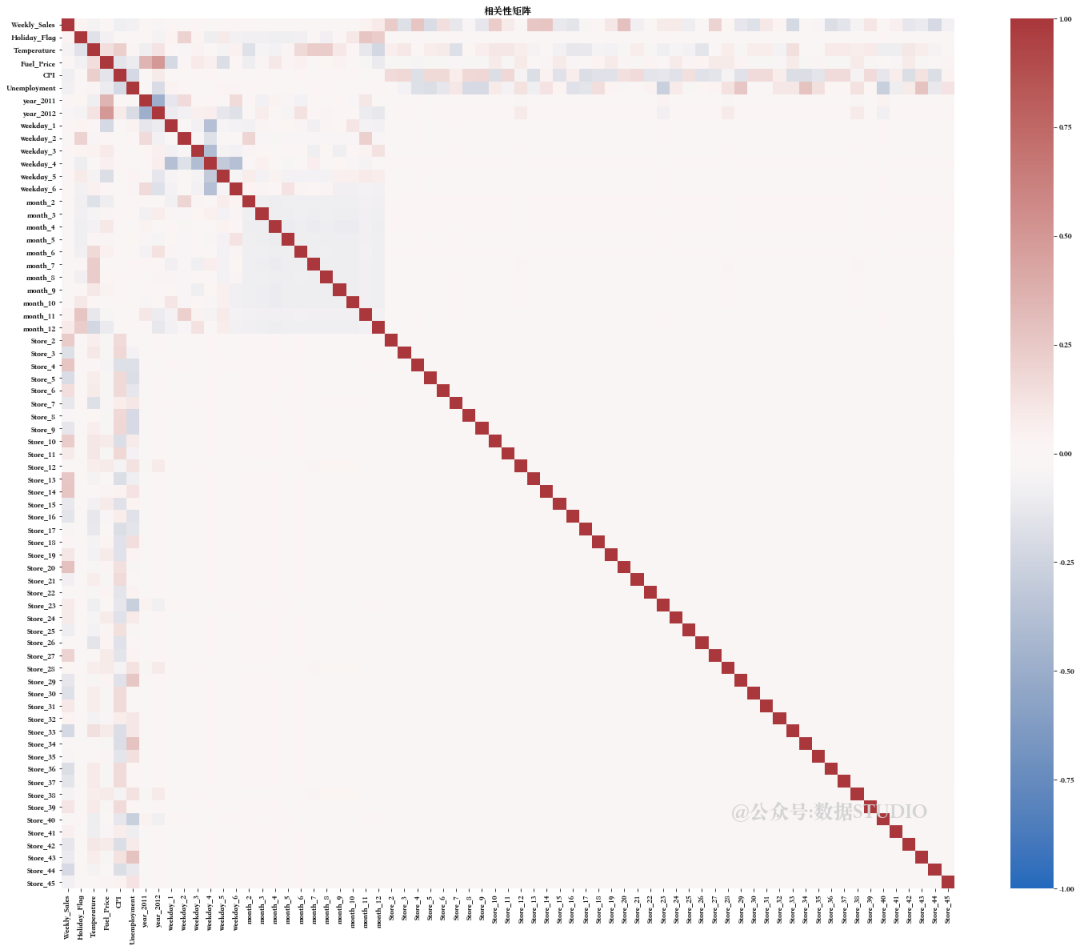
特征之间似乎存在很强的多重相关性。现在需要尝试解决这些问题...

7.1、用统计模型测试线性回归模型

Train_xy = pd.concat([Train_X_std,Train_Y.reset_index(drop=True)],axis=1)
a = Train_xy.columns.valuesAPI = api.ols(formula='{} ~ {}'.format(target,' + '.join(i for i in Train_X.columns)), data=Train_xy).fit()
API.summary()

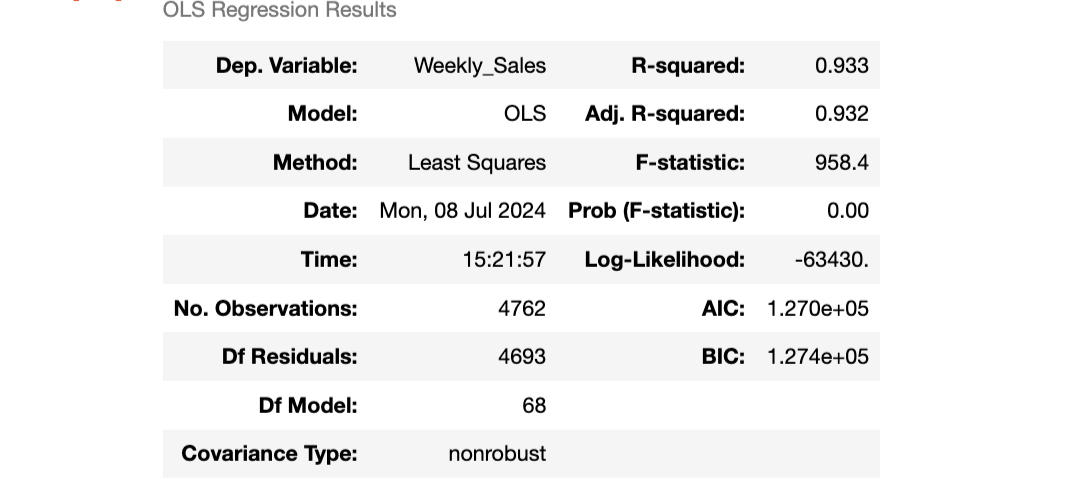
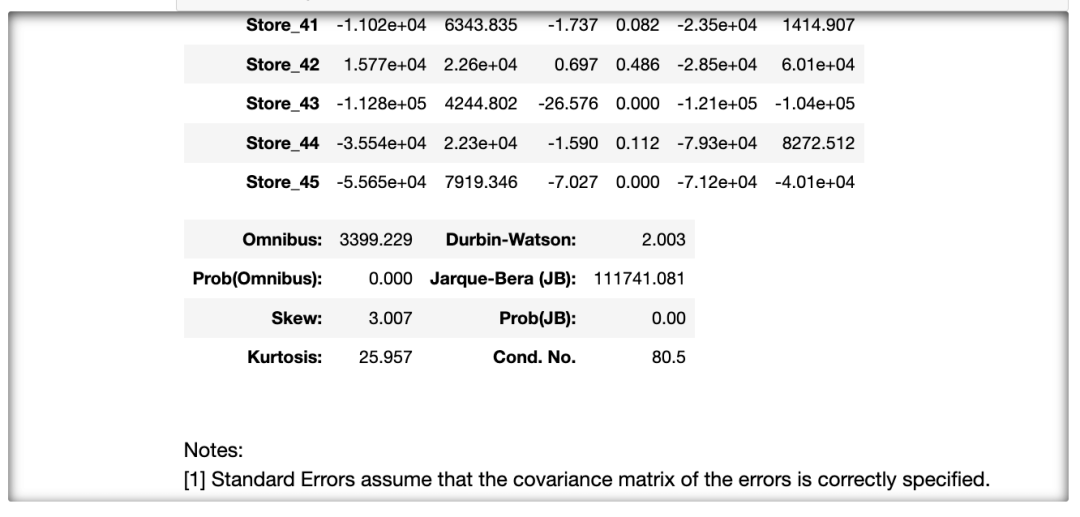
方法：

我们可以通过两种技术来解决多重共线性问题：

手动方法--方差膨胀因子（VIF）
自动方法--递归特征消除法（RFE）
使用 PCA 分解法消除特征

7.2、手动方法--方差膨胀因子（VIF）

from sklearn.preprocessing import PolynomialFeatures
DROP=[]
for i in range(len(Train_X_std.columns)):vif = pd.DataFrame()X = Train_X_std.drop(DROP,axis=1)vif['Features'] = X.columnsvif['VIF'] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]vif['VIF'] = round(vif['VIF'], 2)vif = vif.sort_values(by = "VIF", ascending = False)if vif.loc[0][1]>1:DROP.append(vif.loc[0][0])# 建模LR = LinearRegression()LR.fit(Train_X_std.drop(DROP,axis=1), Train_Y)pred1 = LR.predict(Train_X_std.drop(DROP,axis=1))

Dropped Features -->  ['CPI', 'Unemployment', 'Fuel_Price', 'weekday_4', 'month_7', 'Store_7', 'Temperature', 'month_12', 'Store_43', 'year_2012', 'Store_30', 'month_2', 'month_11', 'Store_16', 'month_5', 'Store_25', 'Store_29', 'month_10', 'Store_17', 'Holiday_Flag', 'Store_18', 'year_2011', 'Store_19', 'month_9', 'Store_20', 'Store_8', 'Store_34', 'Store_15', 'Store_22', 'month_6', 'Store_21', 'Store_35', 'Store_14', 'Store_13', 'Store_45', 'Store_27', 'month_3', 'weekday_1', 'Store_23', 'Store_44', 'Store_42', 'Store_11', 'weekday_5', 'Store_39', 'weekday_2', 'weekday_3', 'Store_24', 'Store_41', 'Store_40', 'Store_10', 'Store_36', 'Store_9', 'month_4', 'Store_2', 'Store_3', 'Store_6']

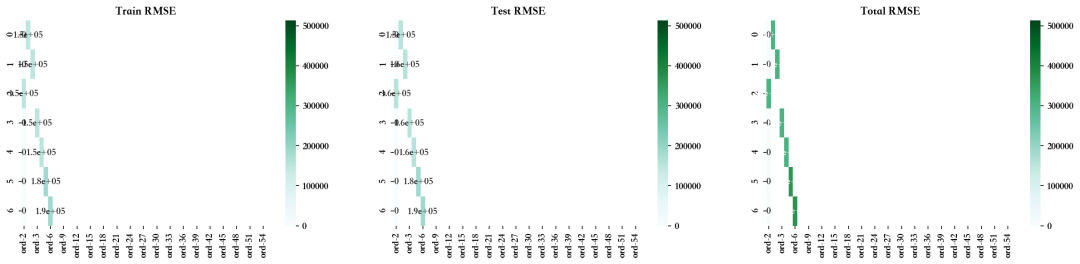
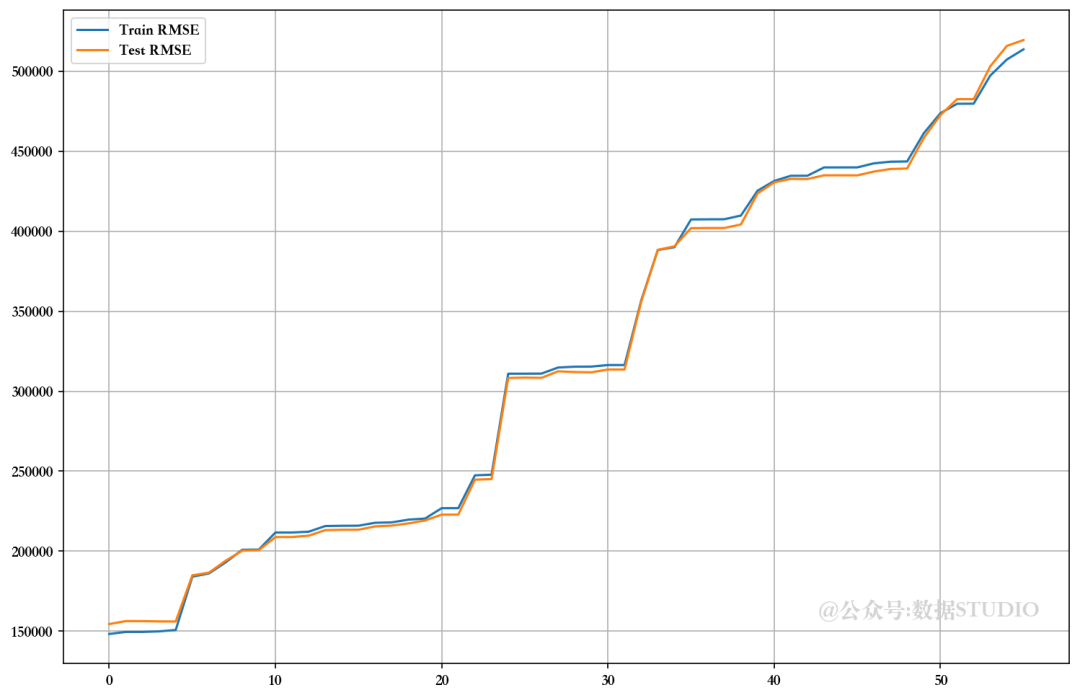
7.3、自动方法--递归特征消除法（RFE）

from sklearn.preprocessing import PolynomialFeatures
Trr=[]; Tss=[]; n=3
m=df.shape[1]-2
for i in range(m):lm = LinearRegression()rfe = RFE(lm,n_features_to_select=Train_X_std.shape[1]-i)rfe = rfe.fit(Train_X_std, Train_Y)# 建模LR = LinearRegression()LR.fit(Train_X_std.loc[:,rfe.support_], Train_Y)pred1 = LR.predict(Train_X_std.loc[:,rfe.support_])

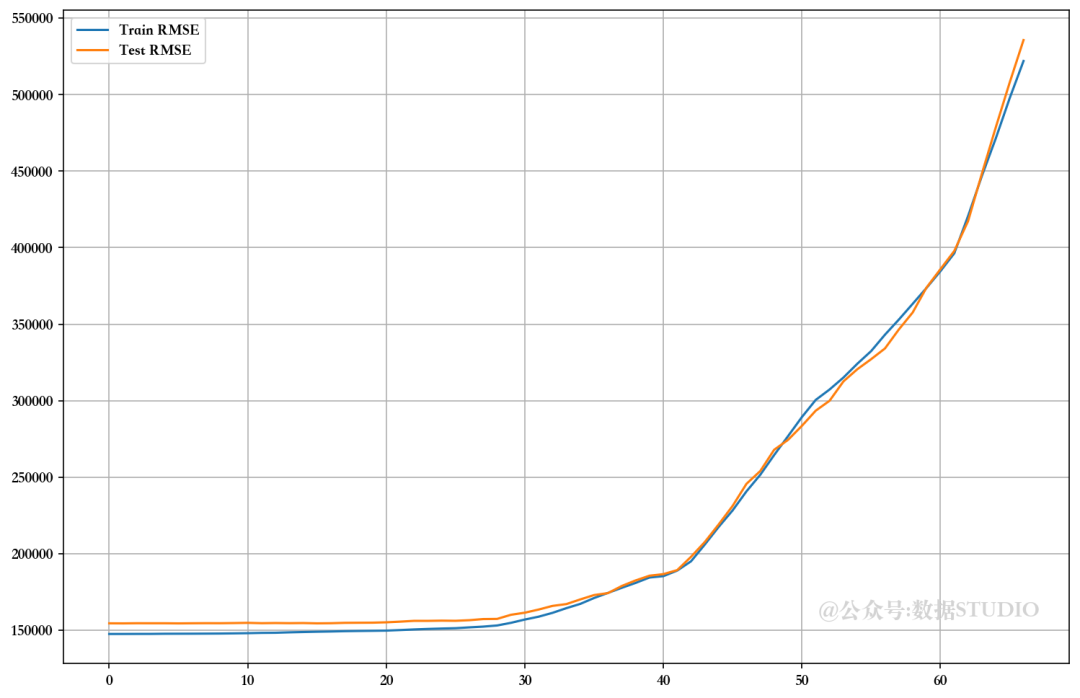
7.4、使用 PCA 分解法消除特征

from sklea.decomposition import PCApca = PCA().fit(Train_X_std)
pca.explained_variance_ratio_ # 解释方差
np.cumsum(pca.explained_variance_ratio_ # 累计解释方差
pca.n_components_ #主成分

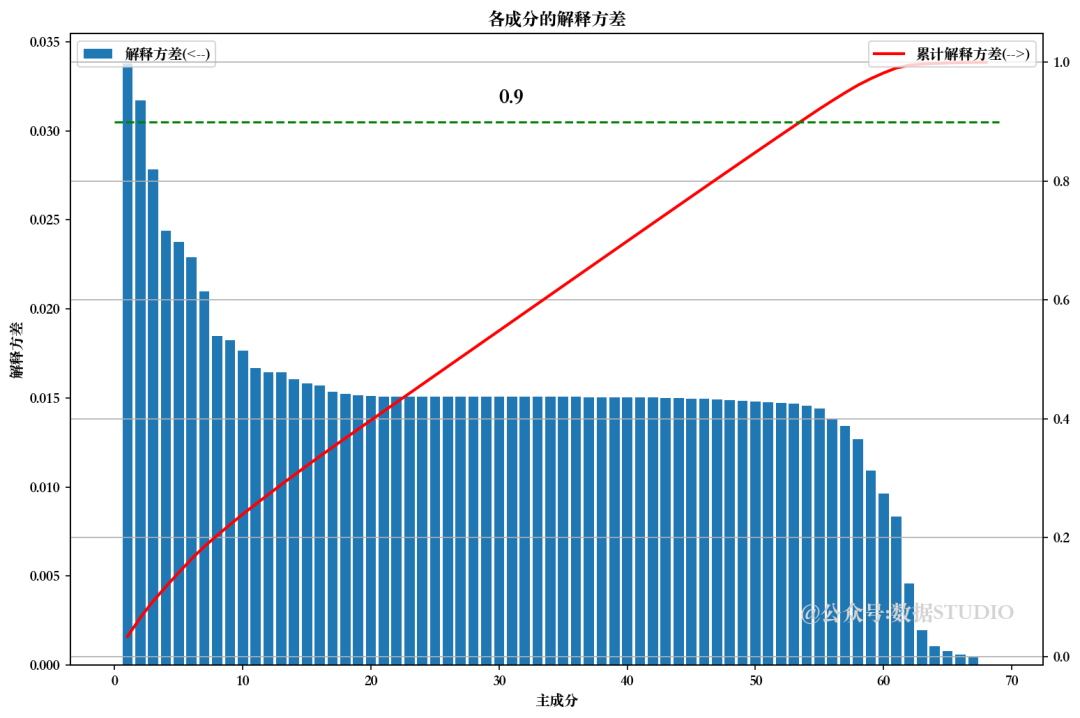
from sklearn.decomposition import PCA
from sklearn.preprocessing import PolynomialFeatures
Trr=[]; Tss=[]; n=3
order=['ord-'+str(i) for i in range(2,n)]
Trd = pd.DataFrame(np.zeros((10,n-2)), columns=order)
Tsd = pd.DataFrame(np.zeros((10,n-2)), columns=order)
m=df.shape[1]-1for i in range(m):pca = PCA(n_components=Train_X_std.shape[1]-i)Train_X_std_pca = pca.fit_transform(Train_X_std)Test_X_std_pca = pca.fit_transform(Test_X_std)# 建模LR = LinearRegression()LR.fit(Train_X_std_pca, Train_Y)pred1 = LR.predict(Train_X_std_pca)

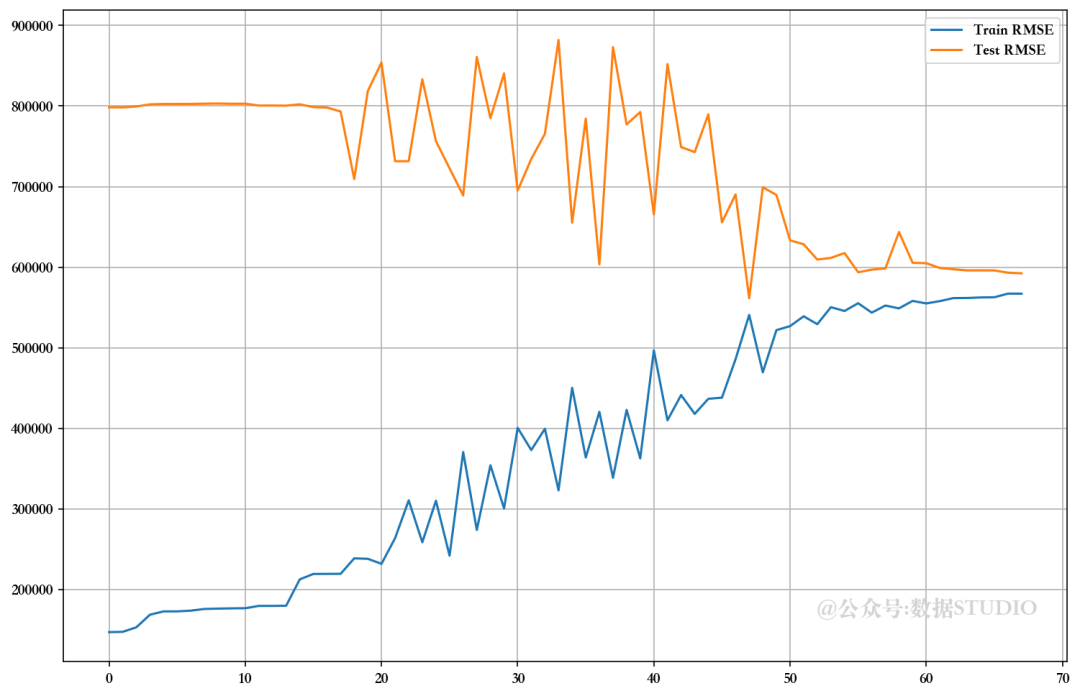
可以看出，在未使用 VIF、RFE 和 PCA 技术放弃特征的情况下，模型的性能相当。比较 RMSE 图，发现使用手动 RFE 技术丢弃大多数特征的最佳值。但由于高级多重线性算法可以解决多重共线性问题，因此我们暂且跳过这些问题。

7.5、筛选出所选特征（RFE ）

lm = LinearRegression()
rfe = RFE(lm,n_features_to_select=Train_X_std.shape[1]-28) 
rfe = rfe.fit(Train_X_std, Train_Y)LR = LinearRegression()
LR.fit(Train_X_std.loc[:,rfe.support_], Train_Y)
pred1 = LR.predict(Train_X_std.loc[:,rfe.support_])
pred2 = LR.predict(Test_X_std.loc[:,rfe.support_])print("训练集MSE:", np.sqrt(mean_squared_error(Train_Y, pred1)))
print("测试集MSE:",np.sqrt(mean_squared_error(Test_Y, pred2)))Train_X_std = Train_X_std.loc[:,rfe.support_]
Test_X_std = Test_X_std.loc[:,rfe.support_]

训练集MSE: 152984.3455868294
测试集MSE: 157283.79051514965

8、预测建模

首先，定义一个函数来评估模型。

Model_Evaluation_Comparison_Matrix = pd.DataFrame(np.zeros([5,8]), columns=['Train-R2','Test-R2','Train-RSS','Test-RSS','Train-MSE','Test-MSE','Train-RMSE','Test-RMSE'])
rc=np.random.choice(Train_X_std.loc[:,Train_X_std.nunique()>=50].columns.values,2,replace=False)
def Evaluate(n, pred1,pred2):"""在实际数据点旁边绘制预测的预测值 """

现在，尝试建立多元回归模型并比较其评估指标，以选择训练集和测试集的最佳拟合模型...

8.1、多元线性回归

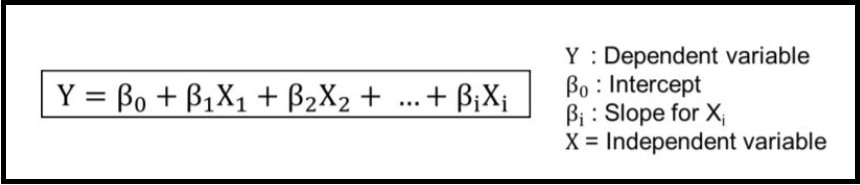
MLR = LinearRegression().fit(Train_X_std,Train_Y)
pred1 = MLR.predict(Train_X_std)
print('回归模型的截距为 ',MLR.intercept_)
Evaluate(0, pred1, pred2)

<<<------------------------------[1m 评估多元线性回归模型 [0m------------------------------>>>回归模型的截距为  1047603.298112138

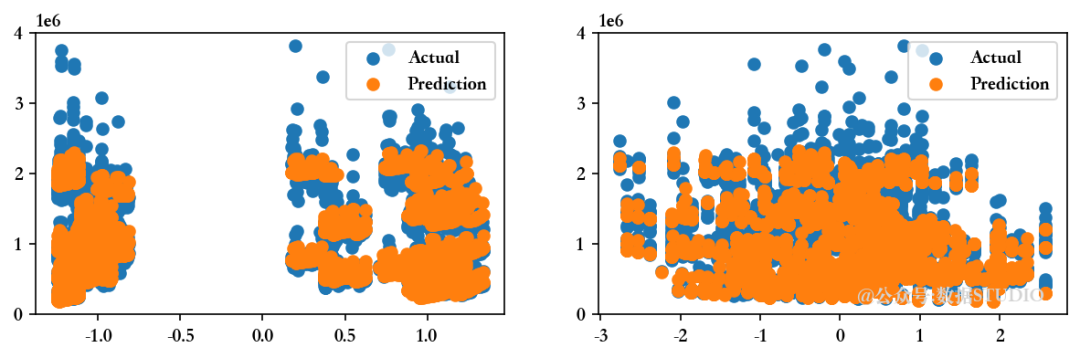
--------------------训练集指标--------------------训练集的 R2 分数  ---> 0.9276826744775732
训练集的残差平方和 (RSS)  ---> 111450847994430.22
训练集的均方误差 (MSE)    ---> 23404209994.630455
训练集的均方根误差 (RMSE) ---> 152984.3455868294--------------------测试集指标--------------------测试集的 R2 分数 ---> 0.927676279121959
测试集的残差平方和 (RSS)  ---> 29463185193746.86
测试集的均方误差 (MSE)   ---> 24738190758.813484
测试集的均方根误差 (RMSE) ---> 157283.79051514965--------------------残差图--------------------

8.2、岭回归模型

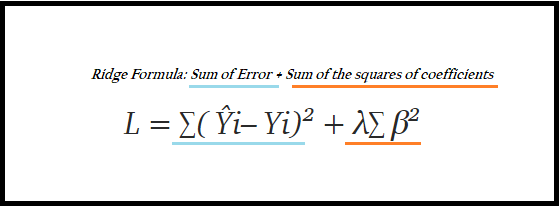
RLR = Ridge().fit(Train_X_std,Train_Y)
pred1 = RLR.predict(Train_X_std)
print('回归模型的截距为 ',MLR.intercept_)
Evaluate(1, pred1, pred2)

<<<-----------------------------------[1m 评估岭回归模型 [0m----------------------------------->>>回归模型的截距为  1047603.298112138

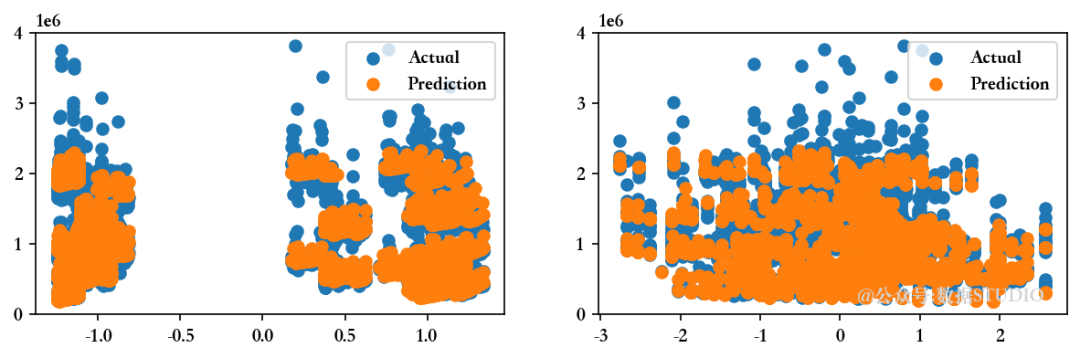
--------------------训练集指标--------------------训练集的 R2 分数  ---> 0.9276821973327432
训练集的残差平方和 (RSS)  ---> 111451583339598.72
训练集的均方误差 (MSE)    ---> 23404364414.02745
训练集的均方根误差 (RMSE) ---> 152984.85027618732--------------------测试集指标--------------------测试集的 R2 分数 ---> 0.927696636618113
测试集的残差平方和 (RSS)  ---> 29454891971661.734
测试集的均方误差 (MSE)   ---> 24731227516.08878
测试集的均方根误差 (RMSE) ---> 157261.65303750554--------------------残差图--------------------

8.3、Lasso 回归模型

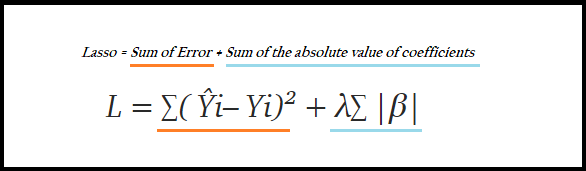
LLR = Lasso().fit(Train_X_std,Train_Y)
pred1 = LLR.predict(Train_X_std)
print('回归模型截距为 ',MLR.intercept_)
Evaluate(2, pred1, pred2)

<<<-----------------------------------[1m 评估回归模型 [0m----------------------------------->>>回归模型截距为  1047603.298112138

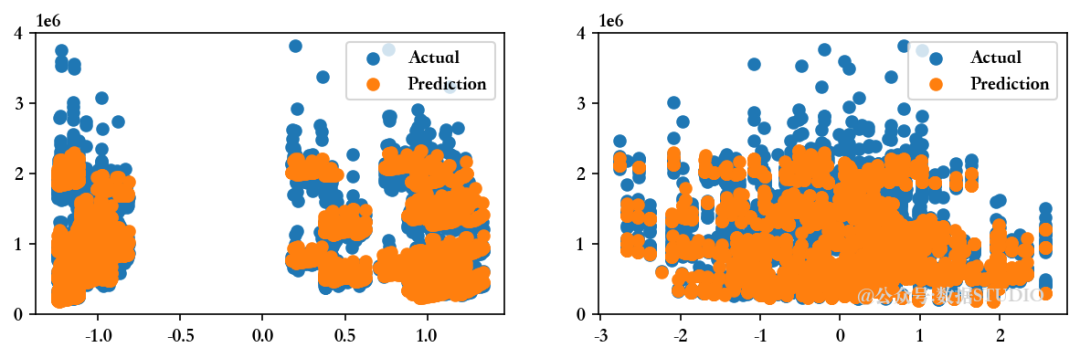
--------------------训练集指标--------------------训练集的 R2 分数  ---> 0.9276826740433101
训练集的残差平方和 (RSS)  ---> 111450848663688.89
训练集的均方误差 (MSE)    ---> 23404210135.171963
训练集的均方根误差 (RMSE) ---> 152984.3460461624--------------------测试集指标--------------------测试集的 R2 分数 ---> 0.9276767498337136
测试集的残差平方和 (RSS)  ---> 29462993435532.15
测试集的均方误差 (MSE)   ---> 24738029752.75579
测试集的均方根误差 (RMSE) ---> 157283.27868135186--------------------残差图--------------------

8.4、弹性网络回归

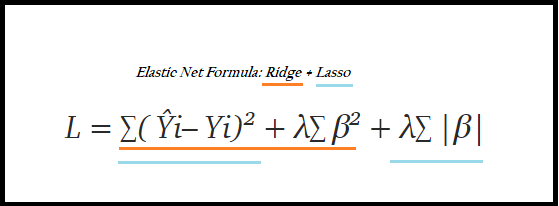
ENR = ElasticNet().fit(Train_X_std,Train_Y)
pred1 = ENR.predict(Train_X_std)
print('回归模型截距为 ',MLR.intercept_)
Evaluate(3, pred1, pred2)

<<<-----------------------------------[1m 弹性网络回归模型 [0m----------------------------------->>>回归模型截距为  1047603.298112138

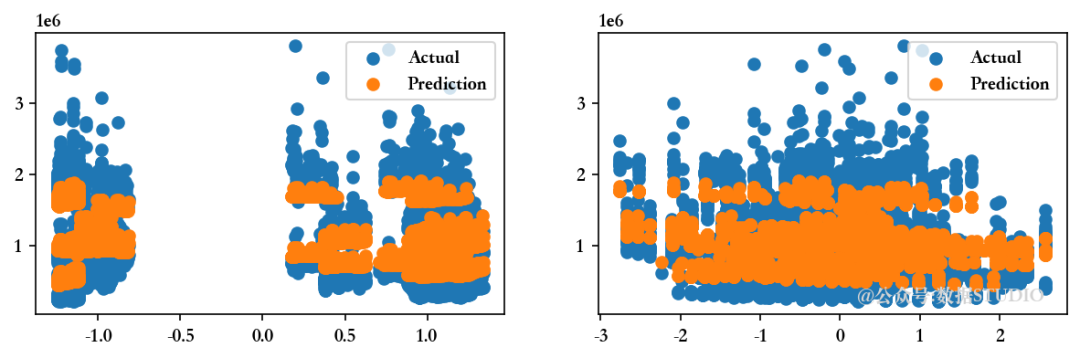
--------------------训练集指标--------------------训练集的 R2 分数  ---> 0.7477826893125253
训练集的残差平方和 (RSS)  ---> 388701226876489.0
训练集的均方误差 (MSE)    ---> 81625625131.56006
训练集的均方根误差 (RMSE) ---> 285701.9865726524--------------------测试集指标--------------------测试集的 R2 分数 ---> 0.7599512663907991
测试集的残差平方和 (RSS)  ---> 97790879783118.03
测试集的均方误差 (MSE)   ---> 82108211404.80104
测试集的均方根误差 (RMSE) ---> 286545.3042797963--------------------残差图--------------------

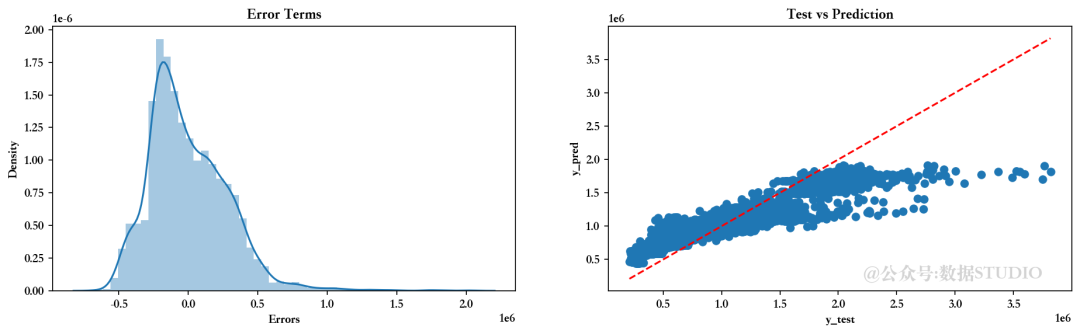
8.5、多项式回归模式

检查不同度数的多项式回归性能

for i in range(2,n_degree):poly_reg = PolynomialFeatures(degree=i)X_poly = poly_reg.fit_transform(Train_X_std)X_poly1 = poly_reg.fit_transform(Test_X_std)LR = LinearRegression()LR.fit(X_poly, Train_Y)pred1 = LR.predict(X_poly)pred2 = LR.predict(X_poly1)

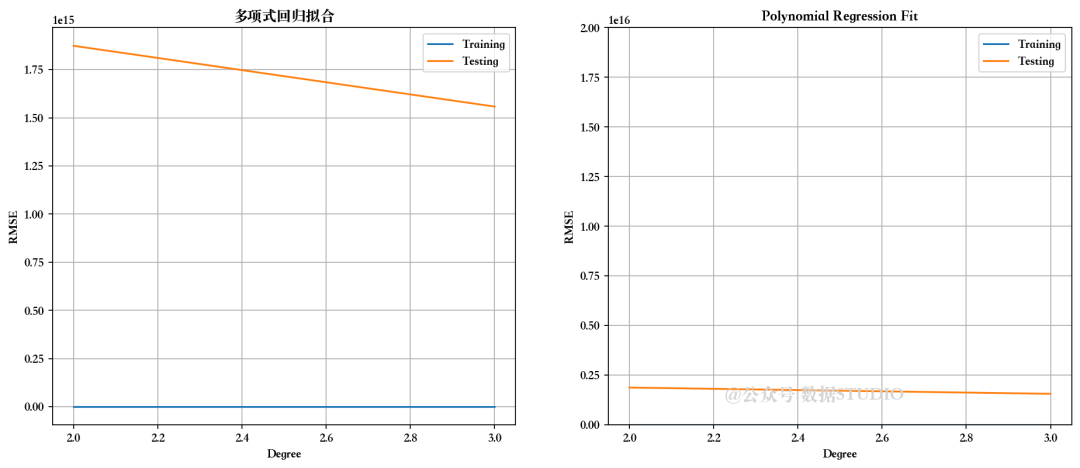
我们可以选择二阶多项式回归，因为它能给出最佳的训练和测试分数。

# 使用二阶多项式回归模型（degree=2）poly_reg = PolynomialFeatures(degree=2)
X_poly = poly_reg.fit_transform(Train_X_std)
PR = LinearRegression()
PR.fit(X_poly, Train_Y)
pred1 = PR.predict(X_poly)
print('回归模型截距为 ',MLR.intercept_)Evaluate(4, pred1, pred2)

<<<-----------------------------------[1m 评估多项式回归模型 [0m----------------------------------->>>回归模型截距为  1047603.298112138

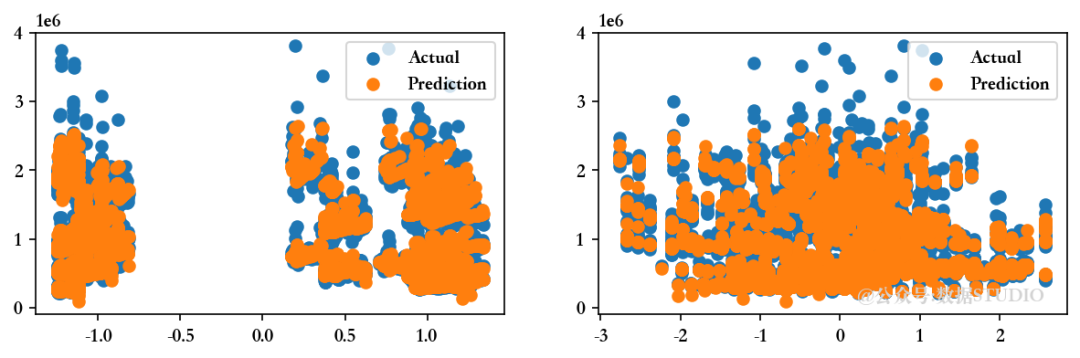
--------------------训练集指标--------------------训练集的 R2 分数  ---> 0.9431089741641003
训练集的残差平方和 (RSS)  ---> 87676819169947.55
训练集的均方误差 (MSE)    ---> 18411763790.413177
训练集的均方根误差 (RMSE) ---> 135689.95464076617--------------------测试集指标--------------------测试集的 R2 分数 ---> -1.0263501127334386e+19
测试集的残差平方和 (RSS)  ---> 4.1811376790307856e+33
测试集的均方误差 (MSE)   ---> 3.5106109815539756e+30
测试集的均方根误差 (RMSE) ---> 1873662451338014.0--------------------残差图--------------------

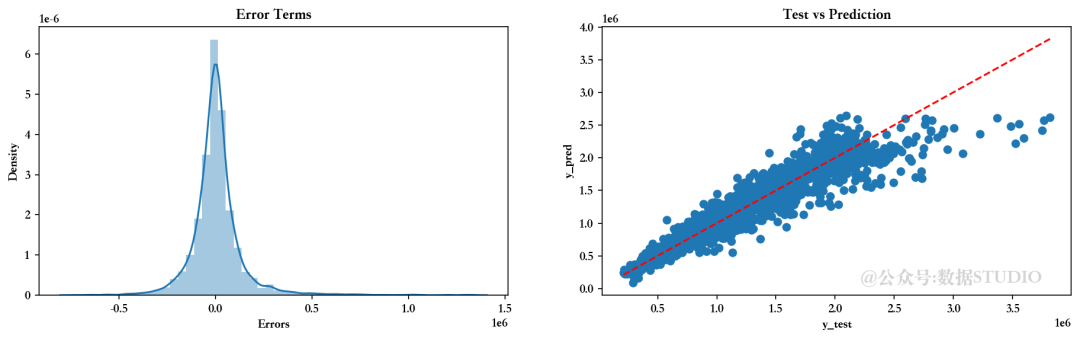
8.6、比较各种模型的评估指标

不同回归模型的 R2 分数对比

EMC = Model_Evaluation_Comparison_Matrix.copy()
EMC.index = ["多元线性回归 (MLR)","岭线性回归 (RLR)","Lasso线性回归 (LLR)","弹性网络回归 (ENR)","多项式回归 (PNR)"]
EMC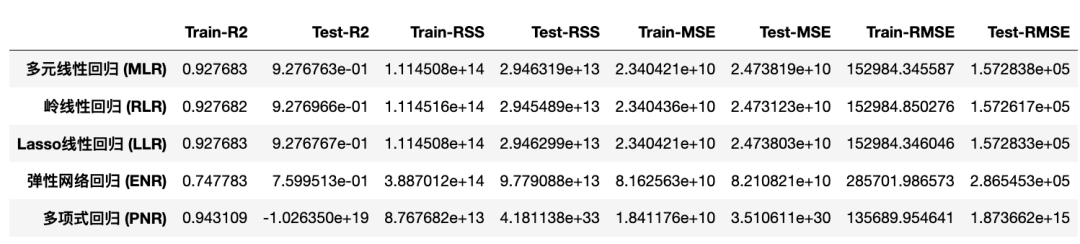

从上图可以看出，多项式回归模型在理解数据集方面具有最高的解释力。

8.7、不同回归模型的均方根误差比较

RMSE 越小，模型越好！而且，前提是模型必须与训练和测试得分非常接近。对于这个问题，可以说多项式回归明显过度拟合了当前问题。令人惊讶的是，简单的多元线性回归模型给出了最好的结果。

9、项目成果和结论

以下是该项目的一些主要内容：

数据集非常小，只有 6435 个样本，经过预处理后，7.5% 的数据样本被删除。
可视化数据分布及其关系有助于我们深入了解特征集。
这些特征具有较高的多重共线性，因此在特征提取步骤中，我们使用 VIF 技术筛选出了合适的特征。
使用默认超参数器测试多种算法，让我们了解了各种模型在这一特定数据集上的性能。
可以肯定的是，多元回归算法比其他算法表现得更好，因为它们的得分不相上下，而且更具通用性。

这篇关于销售预测数据挖掘实战V2.0的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！