反馈时延与端到端拥塞控制

本文主要是介绍反馈时延与端到端拥塞控制，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

先从 越来越无效的拥塞控制 获得一个直感。
开局一张图，剩下全靠编。这是一道习题：

这图来自《高性能通信网络(第二版)》，2002 年的书，很好很高尚，目前这种书不多了。不准备做这道题，但意思要明白，时延越大越不同，系统越震荡，甚至跑飞不稳定，这个道理也可以从相轨迹看出。首先，先看经典的 aimd 收敛图是如何获得的。

aimd 系统的微分方程如下：

$\frac{dW}{dt}=(1-p)\ast \frac{a}{W}-p\ast b\ast W$

系统会稳定在 $(1-p)\ast \frac{a}{W}=p\ast b\ast W$ 处，p 由 buffer 决定，解得 W 为一定值，相平面空间如下：

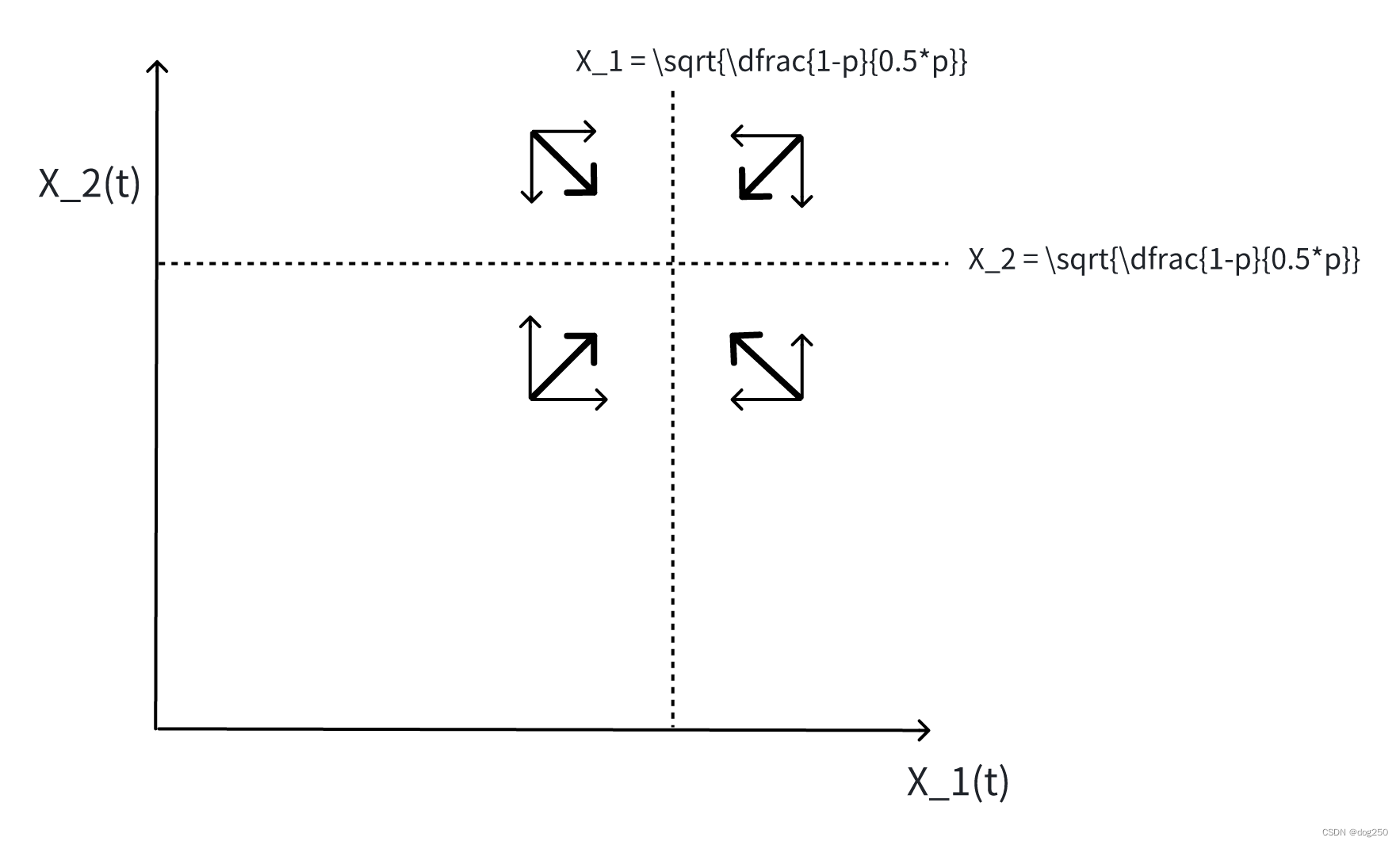
然而若引入一个时滞，即 $W(t)$代换为$W(t-\tau )$，相轨迹就没有这么简单了，大概的意思会变成下面这样：

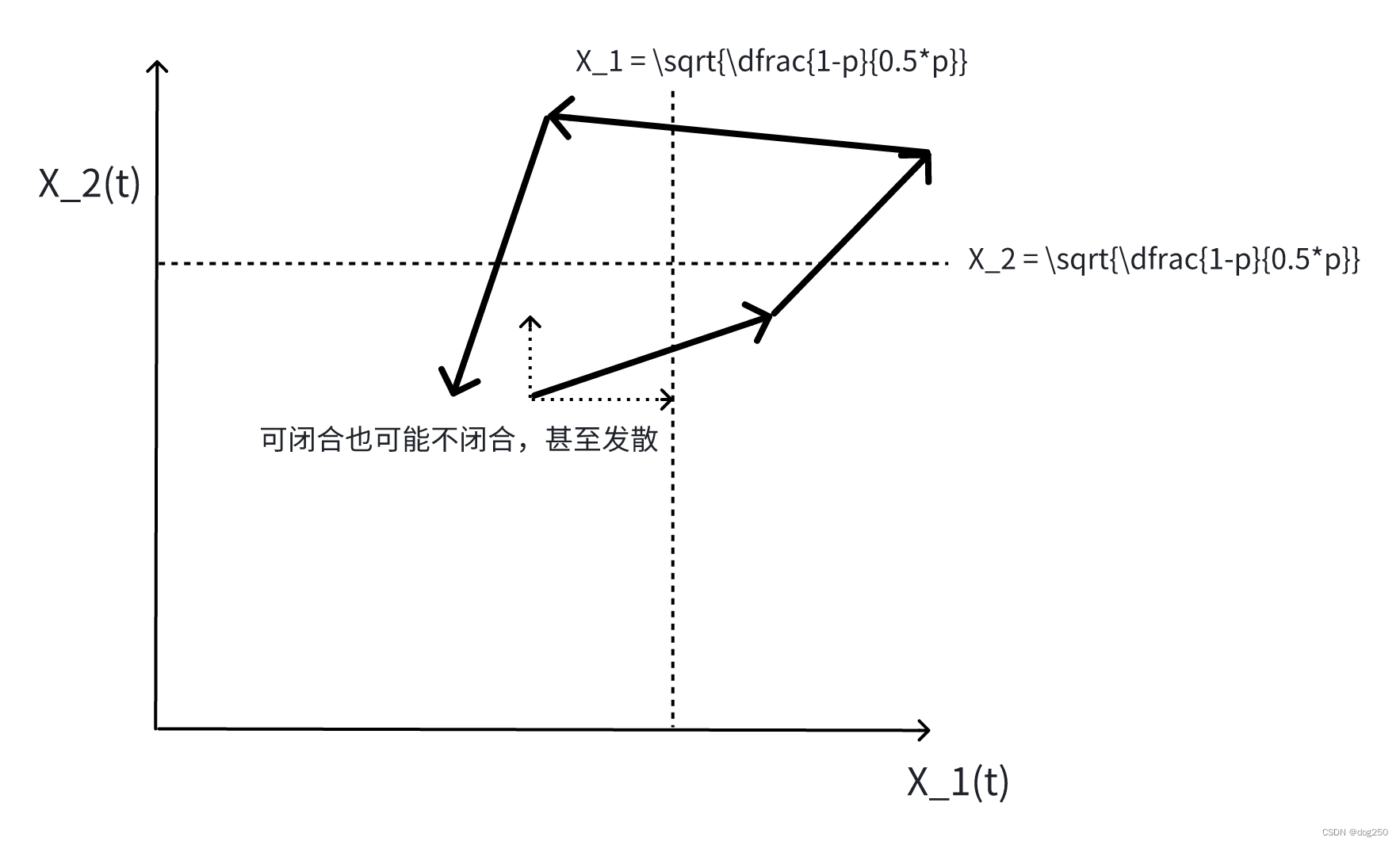
没有时延时，系统的稳定性由 df(x,t)/dt 的符号决定，引入时延后，平衡点的稳定性分析变得更为复杂，需要考虑时延对 f(x,t) 的影响。

时延会导致系统响应滞后。这意味着系统在给定输入的情况下，响应的速度会减慢或产生振荡，这种效应在非线性系统和复杂系统中尤为显著，直接命中网络传输。

简单通俗来讲，rtt 过大时，当 sender 接收到拥塞信号时，拥塞可能已经解除或已经进入第 n 次完全不同的拥塞状态，亦或相反，拥塞状态已经病入膏肓，信号仍未到达 sender，导致持续注入流量加剧拥塞，崩溃是可能的，虽能恢复，但恢复期受震荡周期影响，而震荡周期一般又与反馈时延正相关。

稍微正式一点说，反馈时延过大对控制系统的影响主要体现在系统的稳定性和性能上，基于微分方程分析相轨迹还是太复杂，正规方式是基于系统传递函数分析(涉及拉普拉斯变换)。

控制系统中，传递函数描述输入信号和输出信号之间关系。当反馈时延存在时，系统传递函数会受到影响。假设无时延时系统的传递函数为 G(s)，有时延后的传递函数 G_d(s) 可表示为：

$G_d(s)=G(s)e^{-\tau s}$

这里的 e^{-\tau s} 改变了系统的频率响应和相位特性，影响了系统的稳定性和响应速度。时延会在所有频率上引入一个线性相位滞后，同时，增益曲线也会在高频段出现衰减。

时延的存在还会使根轨迹发生变化，可能导致闭环极点向复平面的不稳定区域移动，从而影响系统的稳定性。

反馈时延还直接影响系统的动态响应，包括上升时间和调整时间。时延越大，系统的响应越慢，动态性能恶化，对干扰和噪声的敏感度增加，这在实时控制和需要快速响应的应用场景中尤其重要。

一个小小的反馈时延，一下子就将一个准线性系统或准一阶，二阶线性系统变成了非线性复杂系统，加上一个时滞就让你无法再用分离变量等方法处理微分方程，更无法在相平面空间施展拳脚(我自信善于此)，从而不得不上传递函数工具，陷入更复杂的数学分析。

我为什么总是反对端到端精确测量，背后就是这个。我强调快速收敛规则而不是精确测量，重点在快速，以确保不会拥塞崩溃，或崩溃后尽快恢复。因此，我在 inflight 守恒算法中强调只保持 “一点点” 对 buffer 的占用，以获得动态性和感知敏感性，我并不觉得过度侵占资源可以获得更高性能或资源利用率，因为整体来看，这种方法代价巨大，即遍从自私的视角来看也是如此，越过 E_best 后，事实上你已经没有收益了。相反，E_best 本身就决定了 buffer 不会占太多。

反思我昨天的 PID 加持 inflight 守恒算法，依然没有占据过多 buffer，但我在 “快速响应” 方面冒了险，还好 PID 还有调参的艺术，效果如何，试试看咯。

进一步反思 aimd，长肥管道 cwnd 恢复慢，大概就是本文所论述的内秉属性，如果想快速恢复，势必会被另一种代价击中另一个软肋。

so aimd-based？大致都是一回事，bbr 就算了，最终它也还是叶落归根。

最后，转发个有趣的：中国移动完成全球最长距离数据快递广域高吞吐技术验证。

浙江温州皮鞋湿，下雨进水不会胖。

这篇关于反馈时延与端到端拥塞控制的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---